4. Мнк при нелинейных моделях

Предположим, что уравнение, связывающее вход и выход исследуемого объекта, нелинейно по параметрам, т.е. имеет вид:

у = F(x, b) (3.4)

Принцип наименьших квадратов легко обобщается и на нелинейный случай. Решением (вектором коэффициентов) задачи среднеквадратичной аппроксимации при нелинейной модели (3.4) будем понимать то значение вектора bЕ^k, для которого сумма квадратов отклонений

(b) =  (F(x_i, b) – y_i)²

принимает минимальное значение. В отличии от линейного случая, в котором минимум находится сравнительно просто – как решение системы линейных уравнений, поиск минимума (b) в общем случае достаточно сложен. В нелинейной модели может существовать несколько локальных минимумов функции (b). По определению МНК-решение соответствует глобальному минимуму.

Линеаризация. В некоторых случаях уравнение (3.4) можно преобразовать к линейному виду:

g(у) = g(F(x, b)) = b₁f₁(x) + … + b_kf_kx). (3.5)

Введя новую переменную z = g(y), получаем обычный МНК. Такая процедура называется линеаризацией. К ней прибегают, когда непосредственная минимизация (b) по каким-либо причинам затруднена. Решить линейную систему намного проще, чем минимизировать сложную функцию.

Пример 3.5. 1) . Положим g(y) = 1/y, получим ax + b = 1/y. Отсюда получим линейный случай:  ( ax_i + b – 1/y_i ) ²  min.

2) . Положим g(y) = ln(y), получим ax + b = ln(y). Отсюда получим линейный случай:  ( ax_i + b – ln(y_i) ) ²  min.

При наличии ошибок в исходных данных преобразование (3.5) обычно приводит к потере точности, т.к. минимизация проводится уже преобразованной суммы квадратов, чье оптимальное значение не соответствует минимуму (b).

Пример 3.6. Истинная зависимость y от х имеет вид: . Имеем данные эксперимента при наличии случайных ошибок : x_i = 0.8, 1,…, 3; у = (1.496, 1.039, 0.57, 0.5141, 0.5428, 0.3272, 0.2415, 0.2065, 0.374, 0.1348, 0.091, 0.2631) (см. рис. 3.4). В результате линеаризации получили модель

.

Рис. 3.4. – истинная зависимость;

   – экспериментальные данные примера 3.6

Результаты аппроксимации приведены на рис. 3.5 и 3.6. Из рис. 3.6 видно, что при начальных значениях х погрешность аппроксимации особенно велика.

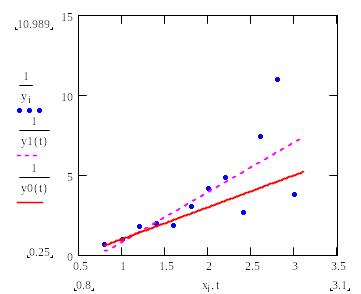
Рис. 3.5. Результат линеаризации примера 3.6

– обратная истинная зависимость;

– МНК-аппроксимация ах + b;

   – экспериментальные данные (обратные величины)

Рис. 3.6. Линеаризованный МНК

– истинная зависимость примера 3.6

   – экспериментальные данные

– результат МНК-аппроксимации

Взвешенный МНК. Расхождение между истинным значением функции и ее аппроксимацией, полученной в результате линеаризации, можно значительно уменьшить с помощью введения соответствующих весов _i для экспериментальных точек, т.е. минимизировать сумму:

₁(b) = _i² (g(F(x_i, b)) – g(y_i)) ² .

Опишем соответствующую процедуру, предложенную С. А. Айвазяном.

Предположим, что экспериментальные значение у представляют собой сумму у = F(x, b) + . Разложим функцию g(y) по формуле Тейлора до линейных членов  в окрестности F(x, b), положив

g(y) = g(F(x, b) + )  g(F(x, b)) + g’_y  = b₁f₁(x) + … + b_kf_k(х) + g’_y .

Отсюда

.

Так как в МНК минимизируют сумму _i ², то получаем

₁ (b) =  [b₁f₁(x_i) + … + b_kf_k(х_i) – g(y_i) ]² ,

т.е. . В матричной записи МНК это означает умножение каждой строки линеаризованной матрицы Ф и вектора g(y) на _i, или умножение матрицы Ф и g(y) слева на диагональную матрицу R, в которой R_{i i} = _i.

Рис. 3.7. Результат применения процедуры Айвазяна к примеру 3.6.

– истинная зависимость;

– взвешенная МНК-аппроксимация

Результат применения процедуры Айвазяна к примеру 3.6 изображен на рис. 3.7 (сравните с рис. 3.6). Получена аппроксимация .