Контрольные вопросы и задания

1. Запишите в явном виде обобщенную схему Горнера.

2. Почему для успешного применения обратной интерполяции требуется, чтобы функция f(x) была монотонна на [a, b].

3. Объясните, почему х* = Q_n (0) – приближенный корень уравнения f(x) = 0 (почему Q(0)).

4. В следующих вариантах на заданных интервалах изменения х с помощью пересчета значения функции с шагом h

а) решить уравнение с точностью  = 10^–5 по функции методом обратной 4-х точечной интерполяции

б) найти экстремум функции с заданной точностью  по аргументу методом параболической интерполяции.

В отчете укажите результаты всех итераций.

1. а)

x [3.1; 6]; h = 0.5;

б) max

x [2.5; 5.5]; h = 0.5;  = 0.001

2. a) x⁴ + 4 x³ – 8 x² – 17 = 0

x [0; 3.5]; h = 0.5;

б) max

x [0; 4]; h = 0.5;  = 0.001

3. a) 2 x⁴ – x² = 10 – exp(x)

x [–3; –0.5]; h = 0.5;

б) min

x [–1; 2]; h = 0.5;  = 0.002

4. a) exp(– 2 x) = 2 x + 10

x [–3; 0.5]; h = 0.5;

б) min

x [0; 4]; h = 0.5;  = 0.005

5. a) 2 exp(x) = 5 x + 2

x [0.5; 4]; h = 0.5;

б) max

x [0; 4]; h = 0.5;  = 0.005

6. a) 1 + 2 x = 10 ^{2 – x}

x [0; 3.5]; h = 0.5;

б) min

x [0; 4]; h = 0.5;  = 0.005

7. a) (2 – x) exp(x) = 0.5

x [0; 3.5]; h = 0.5;

б) max

x [– 3; 1]; h = 0.5;  = 0.001

8. a)

x [0; 3.5]; h = 0.5;

б) max

x [– 3; 1]; h = 0.5;  = 0.005

9. a) x exp(x) = 4.78

x [0; 3.5]; h = 0.5;

б) min

x [0; 3.5]; h = 0.5;  = 0.001

10. a) x + 1.26 = 0.5 exp(x)

x [0; 2.5]; h = 0.5;

б) max

x [0; 3.5]; h = 0.5;  = 0.005

3. Среднеквадратичное приближение. Метод наименьших квадратов

Пусть, как и в п.1, функция у(х), задана таблицей своих значений в N точках (для удобства мы поменяли нумерацию).

x1	х2	….	xN
y1	у2	….	yN

Требуется найти аппроксимирующую функцию вида

Y(x) = b₁ f₁ (x) + b₂ f₂ (x) + … + b_k f_k (x), (3.2)

где f_j(x) – известные функции (базисные функции); b_j – неизвестные коэффициенты; k < N. В качестве меры близости между у(х) и Y(x) задано условие

,

т.е. в отличие от задачи интерполяции, точного совпадения в узловых точках не требуется. Такая задача называется задачей среднеквадратичного приближения.

Искомые коэффициенты определяются методом наименьших квадратов (МНК). Приведем матричную запись этого метода, как наиболее компактную. Обозначим: Ф = [Ф_ij] = [f_j(x_i)] – матрица размером N  k (структурная или регрессионная матрица); b – вектор искомых коэффициентов; у – вектор значений функции у(х) в узлах х_i. Тогда выражение b₁f₁(x_i) + … + b_kf_k(x_i) = Фb представляет собой N-мерный вектор. Для определения вектора b коэффициентов имеем систему линейных уравнений:

(Ф^TФ) b = Ф^Ty, (3.3)

которую легко решить, например, методом Гаусса. В качестве меры точности полученного решения часто используют величину s_СРЕД = – среднеквадратичная погрешность аппроксимации (b* – найденное решение системы (3.3)).

Пример 3.4. Для данных примера 3.1 методом наименьших квадратов построить аппроксимирующий многочлен 2-й степени.

Имеем f₁ (x)  1; f₂ (x) = x; f₂ (x) = x². Следовательно, матрица Ф имеет вид:

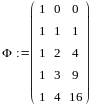
Отсюда

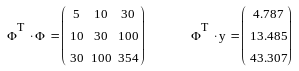
Решив систему (3.3), получим

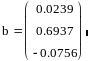
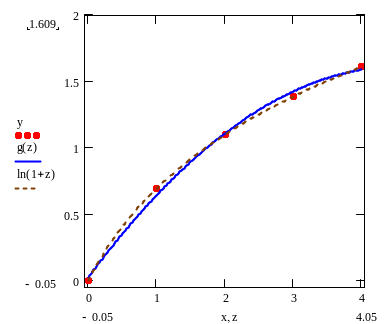
Рис. 3.3. МНК. Графики функций

Y(x) y(x) = ln(1+x)

     узлы аппроксимации

Иными словами, Y(х) = 0.0239 + 0.6937 х – 0.0756 х². На рис. 3.3 изображены графики исходной и аппроксимирующей функций.