13. Кинетическая энергия вращательного движения.

Разобьём абсолютно тв.тело на элементарные объёмы с массами dm_i, которые вращаются вокруг оси z с угловой скоростью w и обладают скоростью V_i.

Е_{кинвращ}=ZЕ_{кинвращi}

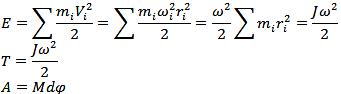
В случае плоского движения кин.энергия тела складывается из кин.энергии поступательного и вращательно движений:

14. Момент инерции. Расчет моментов инерции твердых тел

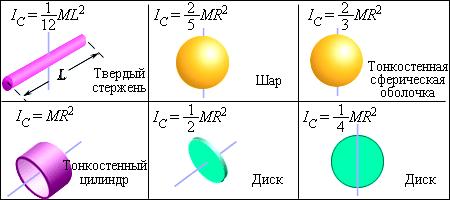
Момент инерции тела относительно оси вращения называется ск.ф.величина, равная сумме произведений массы n мат.точек на квадраты их расстояний до оси вращения: J=Zm_ir_i²

Момент инерции тв.тела – ск.величина, равная сумме моментов инерции всех мат.точек: J_i=m_ir_i²

Х-т распределение массы тела относительно оси вращения.

В случае непрерывного распределения масс эта сумма сводится к интегралу:

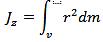
Где интегрирование производится по всему объёму тела.

15. Теорема Штейнера.

Момент инерции тв.тела относительно произвольной оси O’O’ равен сумме момента инерции этого тела относительно параллельной оси ОО, проходящей через центр масс и произведение массы тела на квадрат расстояния между осями:

Применение: Вычислим момент инерции стержня относительно оси, проходящей через конец стержня

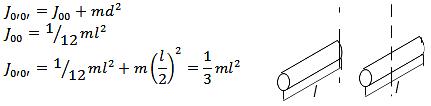
16. Полная механическая энергия. Закон сохранения и изменения полной механической энергии.

Виды мех.энергии: кинетическая, потенциальная

Мех.энергия – ск.величина. х-ся способность тела совершать работу.

Полная мех.энергия системы E равна сумме её кинетической и потенциальной энергий: Е=К+П

Е₂-Е₁=А_{12неконс сил} – закон изменения мех.энергии, т.е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершённой при этом внешними неконс силами.

Системы, в которых мех.энергия постепенно уменьшается за счёт преобразования в др. виды энергии, называются диссипативными (рассеяние энергии).

В диссипативной, изолированной от внешних воздействий, системе сумма всех видов энергии остаётся постоянной (мех, тепловой и тд). Здесь действует общий закон сохранения энергии.

Если внеш. неконс. силы отсутствуют, то Е=К+П=const

Полная мех.энергия замкнутой системы мат.точек между которыми действуют только консервативные силы, остаётся постоянной.

17. Работа постоянной и переменной силы

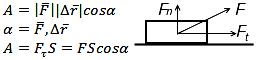
Элементарная работа dA, совершаемая силой при перемещение dr

dA=Fdr=Fcosads=F_tds

Работа, совершаемая силой на конечном пути S, равна алгебраической сумме элементарных (б/м) работ на отдельных б/м участках:

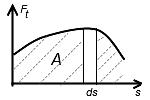Геом. смысл – площадь криволинейной трапеции на графике зависимости силы от пути F_t=f(s)

Сила, действующая на тело, не совершает работу, если:

а) тело покоится (ds=0)

б) сила перпендикулярна направлению перемещения, F_t=0

Если a<90, то работа силы F положительна. Силу называют движущей силой. Если a<90, то работа силы отрицательна. Сила сопротивления.

1 Дж – работа, совершаемая силой в 1Н на пути в 1 м: 1Дж=1Нм

1кал=4,18Дж, 1Втчас=3600Дж

Если на систему действуют неск. Сил, то работы суммы сил, действующих одновременно на мат.точку, равная сумме работ, которую каждая из сил совершала бы в отдельности: А=А₁+А₂+…+А_n – полная работа.