3.3 Замедление нейтронов в средах

Целью рассмотрения замедления нейтронов в средах является, прежде всего, определение асимптотической формы спектра замедления для усреднения сечений и их функционалов вида:

<Σ>=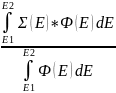 (3.8)

Замедление нейтронов в средах формально надо рассматривать для нескольких случаев для ядер с А=1 и А ≠1, а также с Σ_а =0 и Σ_а ≠0 как это показано в таблице.

	А=1	А>1
Σа =0	Х
Σа ≠0

Для понимания процесса целесообразно вначале изучить спектр нейтронов, испущенных источником в бесконечной гомогенной среде с чисто упругим рассеянием без поглощения, а затем ввести поправки, связанные с наличием поглощения, утечки и отклонениями от простейшего закона рассеяния. Сначала рассмотрим замедление нейтрона в водороде, предположив, что в среде нет поглощения. Первый случай выделен в связи с тем, что массы сталкивающихся частиц одинаковы и нейтрон в одном акте рассеяния может потерять всю кинетическую энергию.

Итак, рассмотрим бесконечную гомогенную среду без поглощения, состоящую из атомов водорода с равномерно распределенными источниками нейтронов. Объемную скорость генерации нейтронов с энергией Е₀ этими источниками обозначим S₀(E₀) нейтр/(см³*с*эВ).

Для нахождения энергетического распределения нейтронов воспользуемся уравнением баланса замедляющихся нейтронов в интервале энергии dE’’ см.рис. 3.4.

Отметим, что получение достаточно строгого решения возможно только для моноэнергетического источника с энергией Е₀.

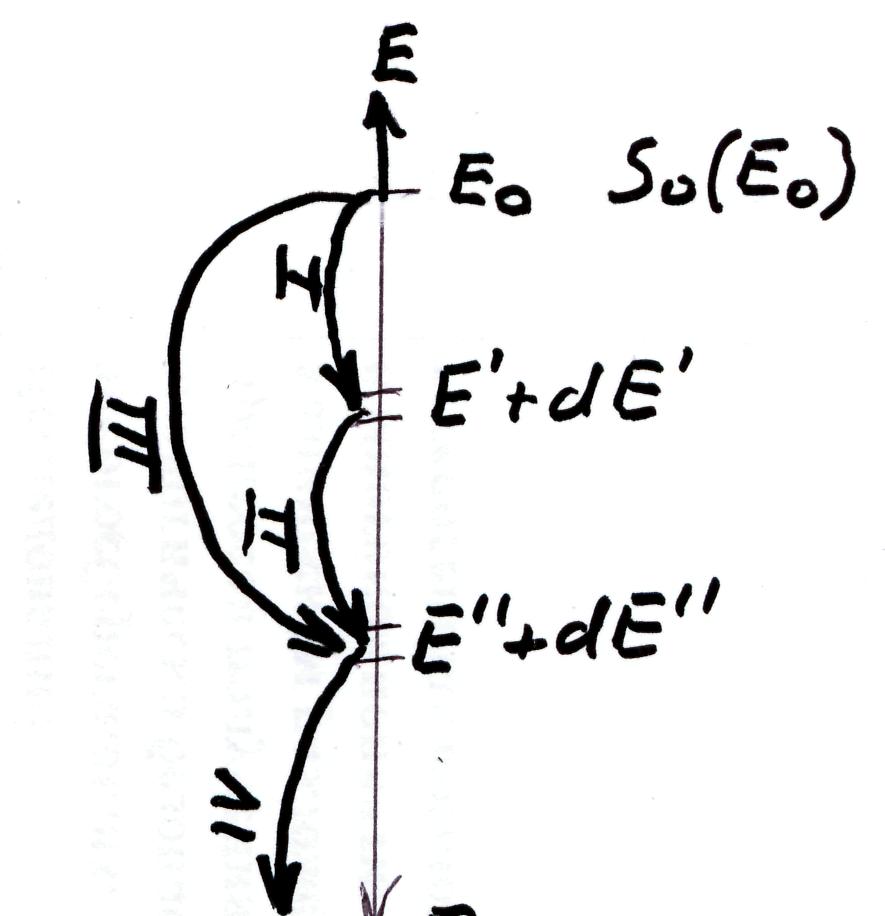
Рис. 3.4. Схема замедления нейтронов

Обозначим Ф(E) поток нейтронов, энергия которых лежит внутри интервала E~E+dE.aΣ_S — макроскопическое сечение рассеяния.

1. Нейтроны источника могут рассеяться в интервал E’+dE’ по ветке I.

2. Нейтроны из интервала E’+dE’могут рассеяться в интервалE’’+dE’’ по ветке II.

3. Нейтроны источника могут рассеяться прямо в интервал E’’+dE’’ по ветке III.

4. Нейтроны из интервала E’’+dE’’могут рассеяться в более низкие энергии по ветке IV.

Составим балансы нейтронов для этих веток.

1. Приход нейтронов источника составляет S₀dE’/E₀ ;

2. Убыль нейтронов определяется скоростью реакции рассеяния Σ_sФ(Е’)dE’;

Вероятность попадания из диапазона Е’+dE’ в диапазон E’’+dE’’ равна p(E’=>E’’) =dE’’/E’;

3. Приход нейтронов источника составляет S₀dE’’/E₀ ;

Приход нейтронов из всех возможных интервалов E’’+dE’’ будет равен интегралу

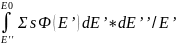
4. Убыль нейтронов определяется скоростью реакции рассеяния Σ_sФ(Е’’)dE’’;

В итоге баланс нейтронов для интервала E’’+dE’’ составит:

Σ_sФ(Е’’)dE’’ = +S₀dE’’/E₀ (3.9)

Это уравнение называется уравнением замедления в среде (правда только для водорода без поглощения).

Сократим уравнение на dE’’, поменяем в интеграле пределы интегрирования:

Σ_sФ(Е’’) = -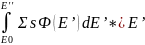 +S₀ /E₀

Введем скорость реакции замедления R_s (E)= Σ_sФ(Е), и переобозначим Е’’ просто Е тогда:

R_s (E)= -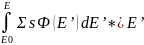 +S₀ /E₀

Продифференцируем уравнение

dR_s (E)= -R_s (E)* dE/E +0

или

dR_s (E)/ R_s (E) = - dE/E

dln(R_s (E) ) = -d ln(E)

Интегрируем:

ln(R_s (E) )=- lnE +ln C

ln(R_s (E)*E) =lnC

Следовательно:

Σ_sФ(Е) *Е=С

Окончательно

Ф(Е) =С/ (Σ_s*Е)

Без доказательства С= S_0:

Ф(Е) =S₀С/ (Σ_s*Е) (3.10a)

Мы достигли своей главной цели- определили форму асимптотического спектра замедления в среде(водорода без поглощения) и этот спектр Ф(Е) =1/ (Е) называется спектром Ферми.

Реальный спектр без предыдущих предположений будет, конечно сложнее и имеет вид для ядер с А >1:

Ф(Е) =S₀С/ (ζ*Σ_s*Е) (3.10б)

А для любых ядер с поглощением:

Ф(Е)= 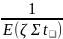EXP{- 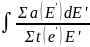} (3.11)