3 Замедление нейтронов

3.1 Общие закономерности

Реактор на тепловых нейтронах отличается от других типов реакторов тем, что после реакции деления нужно замедлить вторичный нейтрон до тепловых энергий (Е< 1 эВ), где он эффективно поглотится топливом и разделит ядро, организуя, таким образом цепную реакцию. В основе замедления нейтрона лежит его упругое рассеяние на ядрах различных материалов и в первую очередь на ядрах замедлителя.

Быстрые нейтроны постепенно отдают свою энергию (замедляются) в результате упругих и неупругих взаимодействий с ядрами. Замедление приводит в конечном счете к тому, что все нейтроны становятся тепловыми.

Па протяжении большей части процесса замедления кинетическая энергия нейтронов значительно превышает как кинетическую энергию теплового движения атомов замедлителя, так и энергию их связи в молекуле или кристаллической решетке. При этом можно не учитывать ни собственного движения рассеивающих ядер, ни молекулярных и химических связей в замедлителе и считать рассеивающее ядро неподвижным и свободным. Такая модель справедлива при энергиях нейтронов выше ~ 1 эВ. Будем рассматривать простейшую элементарную теорию замедления, в которой предполагается, что во всем энергетическом интервале от 1 эВ до 10 МэВ нейтроны теряют свою энергию только в результате упругого сферически симметричного рассеяния на неподвижных и свободных ядрах.

В системе центра инерции С

Основные соотношения между энергией, которую теряет нейтрон в акте упругого рассеяния, и углом, на который изменяется направление его движения,— углом рассеяния нетрудно получить из законов сохранения энергии и импульса. Это задача классической механики и решается она введением системы координат С, связанной с центром инерции ядра и нейтрона, и последующим переходом в лабораторную систему координат L. Состояния нейтрона и ядра в этих двух системах до и после столкновения показаны на рис. 3.1 а-б.

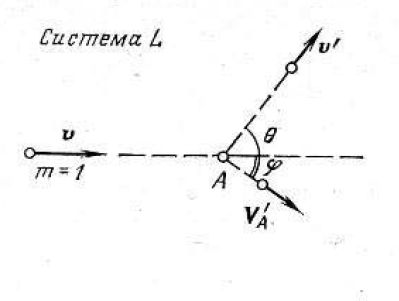
Рис. 3.1. а Рассеяние нейтрона в лабораторной системе координат (L)

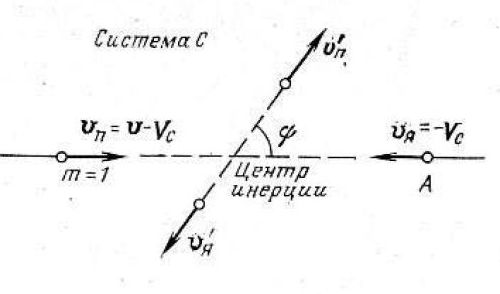
Рис. 3.1.б Рассеяние нейтрона в системе центра инерции (С)

Примем массу покоя нейтрона за единицу, а массу рассеивающего ядра будем считать равной А. По определению в системе С суммарный импульс нейтрона и ядра равен нулю до столкновения и остается равным пулю после столкновения. Обозначив v —скорость нейтрона в системе Lдо столкновения и Vc— скорость системыСотносительно системы L,

Из полученных результатов следует, что в системе центра инерции скорости нейтрона и ядра до и после столкновения соответственно равны между собой и не зависят от угла ψ, который называется углом рассеяния в системе С. В этой системе нейтрон после столкновения летит с равной вероятностью в любом направлении, т. е. имеет место изотропия рассеяния.

В лабораторной системе координат

Рассмотрим акт рассеяния при переходе в в лабораторную систему координат. Используя стандартные преобразования перехода от системы центра инерции к лабораторной получим:

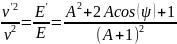(3.1)

Векторная диаграмма скоростей упругого рассеяния в лабораторной системе показана на рис. 3.1.в.

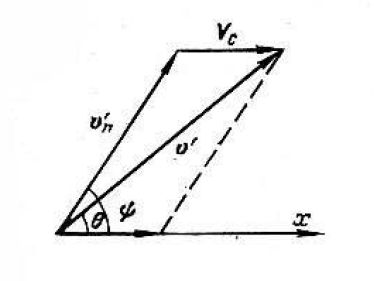
Рис 3.1.в. Векторная диаграмма скоростей

Тогда в лабораторной системе:

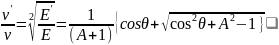(3.2)

Если нейтрон при рассеянии:

• Не изменяет своего первоначального направления (θ = 0), то это скользящий удар, энергия нейтрона при этом не изменяется (Е' = Е).

• Столкновение, при котором нейтрон меняет направление своего движения на обратное (θ = π), это лобовой удар, он приводит к максимальной передаче энергии нейтрона ядру, а отношение энергий принимает минимальное значение, равное:

α =Е^’_min/E= ((A-1)/(A+1))². (3.3)

• Исключением является водород. Действительно, предельный угол рассеяния на водороде (А=1) равен π /2, а отношение Е'/Е = соs²θ . Значение θ = π /2 соответствует полной передаче энергии ядру и остановке нейтрона, т. е. α=0.

• В другом предельном случае (А= ∞) потеря энергии нейтроном стремится к нулю, т. е. Е'/Е=1 независимо от угла рассеяния.

Таким образом, при упругом рассеянии выполняется закон сохранения кинетической энергии нейтрона и рассеивающего ядра и закон сохранения импульса. При этом в случае лобового столкновения ядра и нейтрона происходит потеря энергии нейтрона, равная E = E₀ ((A-1)/(A+1))². Из этой формулы уже можно составить мнение о наилучшем замедлителе, которым является водородосодержащие материалы, и в частности вода.

Рассмотрим потерю энергии ΔЕ в одном акте рассеяния. Эта величина изменяется от нуля до некоторого максимального значения:

ΔЕ_max=E- Е^’_min =E(1- α ) (3.4а)

и она зависит от энергии нейтрона до столкновения и массы ядра-рассеивателя. В то же время относительная потеря энергии при упругом рассеянии нейтрона не зависит от его начальной энергиии составляет определенную долю первоначальной:

ΔЕ_max /Е= (1- α ) = 4А/(А + 1)². (3.4б)

Поскольку ΔЕ является конечно-разностным выражением дифференциала dE, то

ΔЕ_max /Е= Δln(1/E)

Это первый сигнал того, что в теории замедления более перспективно использовать не ΔЕ а dln(1/E)=- dln(E).

Параметр α, как видно, зависит только от массы ядра-мишени. Для водорода α=0, и, следовательно, нейтрон при лобовом ударе теряет всю свою кинетическую энергию. Столкновение нейтрона с другими ядрами приводит лишь к частичной потере энергии.

Энергетический интервал, определенный выражением (3.4а), называется ступенькой замедления. Нейтрон с начальной энергией Е может после столкновения иметь любую энергию в интервале от Е до α *Е. Вероятность для нейтрона с начальной энергией Е замедлиться до энергии E’< α *Е равна нулю.

Нетрудно установить связь между углами θ и ψ .

Из последнего соотношения следует, что при А»1

cos θ≈cosψ

и

θ≈ψ

Таким образом, в средах с тяжелыми ядрами рассеяние в лабораторной системе отсчета близко к изотропному. Чем меньше А, тем заметнее проявляется анизотропия рассеяния. Этот вывод следует также из векторной диаграммы (см. рис. 3.1.в). Действительно, при уменьшении атомной массы ядра-мишени модуль скорости центра инерции Vcувеличивается и угол θ все больше отличается от угла ψ . Наибольшая анизотропия имеет место при рассеянии на водороде: угол рассеяния θ , как об этом уже упоминалось выше, лежит в пределах от 0 до π/2 — нейтрон рассеивается только вперед. Если в системе Lне все направления полета нейтрона после рассеяния равновероятны, то, очевидно, что средний косинус угла рассеяния не будет обращаться и нуль, как это имело место в системе С.

Чем легче ядро, с которым сталкивается нейтрон, тем больше средний косинус угла рассеяния и, следовательно, тем меньше средний угол рассеяния. Это означает, что λ_s,tr>λ_s Σ_s,tr<Σ_s, . Так, при рассеянии на водороде μ= 0.66, и Σ_s,tr= Σ_s,/3.Таким образом, средний косинус угла рассеяния может служить мерой анизотропии рассеяния.

Помимо упругого рассеяния происходит и неупругое рассеяние нейтрона. При неупругом рассеянии часть энергии расходуется на возбуждение одного из энергетических уровней ядра, поэтому кинетическая энергия частиц не сохраняется, и нейтрон теряет значи­тельно больше энергии, чем при упругом рассеянии.

Неупругое рассеяние нейтронов выше 1 МэВ на ядрах железа очень важно для уменьшения потока быстрых нейтронов на корпус реактора ВВЭР, так как боковой отражатель в реакторе ВВЭР состоит в основном из железа и воды (причем железа по объему больше, чем воды). Дело в том что, прочностные свойства корпуса реактора (деградация прочностных свойств корпуса в основном и определяет жизненный цикл блока АЭС с ВВЭР) ухудшаются со временем из-за поглощения и рассеяния в нем быстрых нейтронов с энергией выше 0.5 МэВ. Данные явления приводят к охрупчиванию корпуса и зависят от флюенса быстрых нейтронов на корпус,который определяется следующим выражением:

Ф= 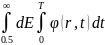(3.5)

Чем больше флюенс нейтронов на корпус, тем сильнее ухудшаются прочностные свойства корпуса реактора ВВЭР. Поэтому если бы не было неупругого рассеяния нейтронов на железе, то флюенс быстрых нейтронов на корпус возрос бы многократно и сущест­венно уменьшил бы жизненный цикл реактора, что, может быть, сделало бы экономически не выгодным их создание.

Что касается упругого рассеяния, то наилучшим замедлителем является водород, затем следует бериллий, тяжелая вода и графит. В мире известны тяжеловодные реакторы (производитель Канада), графитовые реакторы в России (РБМК) и легководяные реакторы по всему миру (ВВЭР, PWR и BWR).

Количественно процесс замедления нейтронов характеризуется длиной замедления L_m, которая равняется среднему расстоянию от точки рождения нейтрона до точки, где он достигает диапазона тепловых энергий (0.02– 1.0 Эв). После достижения тепловых энергий нейтрон не сразу поглощается в уране или другом материале, он может испытывать много столкновений, приходя в тепловое равновесие с ядрами ма­териала замедлителя. При этом нейтрон может как терять энергию, так и приобретать ее. Данный процесс называется термализацией нейтронов. В процессе термализации нейтрон диффундирует в среде замедлителя от точки замедления до точки, где он поглощается каким-либо ядром. Процесс диффузии нейтрона при термализации характеризуется длиной диффузии L_d. Значения L_mи L_dдля различных замедлителей приведены в табл. 3.1.

Таблица 3.1 Длины замедления и диффузии в различных веществах

Вещество	Длина замедления Lm, см	Длина диффузии Ld, см
Вода Тяжелая вода Бериллий Графит	5.3 10.4 8.9 17.7	2.8 116 20.8 53.8

Из данных, приведенных табл. 3.1, следует, что наилучшим замедлителем является вода. Недаром максимальное распространение в мире из всех тепловых реакторов получили водо-водяные реакторы. По этой же причине из всех имеющихся реакторов легководяной реактор занимает наименьший объем. Правда, наибольшее распространение получили реакторы на легкой воде не только потому, что вода наилучший замедлитель нейтронов, но и потому, что она является прекрасным теплоносителем для съема большого количества тепла в реакторе, т.е. вода совмещает одновременно в себе две функции: замедлителя и теплоносителя.

Приведенные в табл. 3.1 данные по замедлению и диффузии нейтронов определяют главные особенности переноса нейтронов в реакторах ВВЭР и ряд явлений, присущих таким реакторам, связанных с этими особенностями.