
- •4.Вычисление длины дуги и объема тела.
- •6. Частная производная и дифференциал функции нескольких переменных.
- •7.Экстремум функции нескольких переменных.
- •10.Производная от сложной фун-и.
- •12. Арифметика числовых рядов.
- •14. Признак сравнения рядов.
- •18. Ряды Макларена для основных элементарных функций.
- •22. Двойной интеграл и его свойства.
- •24. Замена переменной в двойном интеграле.
- •25. Тройной интеграл и его вычисление
- •34. Метод вариации произвольных постоянных.
- •36. Теоремы сложения и умножения для несовместных и независимых событий.
- •37 Теоремы сложения и умножения. Вероятности двух случайных событий.
- •38 Формула полной вероятности. Формула Байеса.
- •39. Математическое ожидание случайной величины и его свойства.
- •42. Плотность распределения и ее свойства.
- •45. Математическое ожидание и дисперсия в распределении Пуассона.
- •46 Вероятностный смысл параметров нормального распределения.
1.Определенный интеграл и его свойства Пусть
f(x) определена на [a;b]. Разобьём [a;b]на
части с несколькими произвольными
точками a = x0 < x1 < x2 < xn = b Тогда
говорят, что произведено разбиение R
отрезка [a;b] Далее выберем произв. точку
Функция f(x) называется интегрируемой на [a;b]. О I.
Величина определенного интеграла не
зависит от обозначения переменной
интегрирования, т.е. II.
Определенный интеграл с одинаковыми
пределами интегрирования равен нулю.
III.
При перестановке пределов интегрирования
определенный интеграл меняет свой
знак на обратный. IV.
Если промежуток интегрирования [a,b]
разбит на конечное число частичных
промежутков, то определенный интеграл,
взятый по промежутке [a,b], равен сумме
определенных интегралов, взятых по
всем его частичным промежуткам. V.
Постоянный множитель можно выносить
за знак определенного интеграла. VI.
Определенной интеграл от алгебраической
суммы конечного числа непрерывных
функций равен такой же алгебраической
сумме определенных интегралов от этих
функций. 11.Дифференциал ф-и нескольких переменных Дифференцируемая функция: Если
полное приращение ф-ции, т.е. величина
Положив
в равенстве 1
|
2.Теорема о среднем значении Если
f(x) - непрерывная функция, заданная на
промежутке [a, b], то существует такая
точка , что
Разделим
на (б-а) все части нер-ва:
Ф-я
f(x)
непрерывна. Значит она принимает все
значения из промежутка [m,M]
в том числе, в какой-то точке С она
принимает w
значения, стоящие внутри нер-ва. Тогда
f(
c)= f( С) – сред.зн.ф-и 4.Об общем виде первообразной Пусть F — какая-нибудь частная первообразная данной функции на интервале I. Тогда общая первообразная функции f на I имеет вид F(x)+C, где C — произвольная постоянная. Док-во: Пусть G(x) –любая первообразная ф-и f. По определению первообразной имеем F’(x)=f(x) и G’(x)=f(x) тождественно на I, а так как ф-и с тождественными производными отличаются на константу , имеем G(x)=F(x)+C, гдеС константа. 5.Основные методы вычисления интегралов 1.Формулой
Ньютона-Лейбница. Применяется метод
во всех случаях, когда может быть
найдена первообразная ф-и F(x)
для подынтегральной ф-и f(x).
2.Замена
переменной. Делается подстановка x= 2.
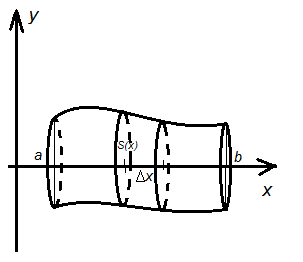
множеством значений ф-и x= 7. Вычисление объема с помощью интеграла Формула вычисления объема тела Пусть в каждой точке х есть S поперечного сечения, тогда V тела, ограниченного двумя близкими областями, расположенными на расстоянии х, V цилиндра с высотой n=x, и Sосн=S(ci), где сi[x; x+x] Объем
тела
В
|
||||||||||||||||||||||||||||
8. Несобственный интеграл и его свойства
Всякая непрерывная функция на отрезке ограничена. Пусть
Интеграл
с бесконечным верхним пределом -
Если нет или равен , то назыв. расходящимся. Если
предел существует и конечный –
сходящимся.аналогично опред.инт.с
∞нижним пределом.можно дать опред. Свойства интегралов с бесконечным пределом интегрирования: 1.
2.
Если
Если расходится, то тоже расходится. Рассм. 22.Расходимость гармонического ряда Гармоническим
рядом называют сумму бесконечного
количества членов обратных
последовательным числам натурального
ряда. Его обозначают Докажем расходимость гармонического ряда. Если После
сложения членов левой части неравенств
получим 25.Абсолютная сходимость рядов Теорема.
Если ряд
Док-во:рассм.вспомогательный
ряд (u1+|u1|)+(u2+|u2|)+… Если сходится (6),то (1)наз. Абсолютно сходящимся,если же (1)сход,а(6) расх,то (1)-условно сходящийся. 21. Необходимый признак сходимости ряда. Если
ряд сходится, то
Док-во:
Рассмотрім 2 частные суммы
Следствие1.
Если
Следствие2.
Если в ряду
Док-во:
Пусть ряд
1 сходится и
его частичные суммы
|
12. Метод наименьших квадратов. Случай линейной зависимости. Его применение в химии. пусть задана таблица
Рассм.
Хк и ук,как прямоугольные декартовы
координ.точек на плоскости
М1(х1,у1),М2(х2,у2)…Mn(xn,yn)
предположим,что эти точки лежат на
какой-то прямой и между х и у есть
линейная зависимость:у=ах+в(1),где а и
в-параметры,значение
кот.необх.опред-ь.итак,ах+в-у=0(2).т.к.
Мк(хк,ук) только ≈ лежат на
прямой,определяемой ур. (1)→подставляя
в (2)такбличные хк и ук(к=1,2,…),получ. Нужно
подобрать ф и в так,чтоб Е были как
модно малы по абсолютной величине.согластно
методу маим.квадратов подберем а и в
так,чтоб :u=
13. Метод наименьших квадратов. Случай квадратичной зависимости. Его применение в химии. пусть задана таблица
Рассм. Хк и ук,как прямоугольные декартовы координ.точек на плоскости М1(х1,у1),М2(х2,у2)…Mn(xn,yn) предположим,что эти точки лежат на какой-то параболе и между х и у есть ≈ квадратичная зависимость:у=ах2+вх+с(1),где а,в,с-параметры,знач.кот.нужно опред. В
правую часть подставим вместо х
табличные значения хк
,тогда полчим числа zk=axk2+bxk+c.было
бы идеально подобрать знач.параметров
а,в,с так,что при всех к оказалось
zk=yk(к=1,2…n)но
при n>3
это сдлеать нельзя,т.к. знач а,в,с
найдены из ур-я:y1=ax12+bx1+c,
y2=ax22+bx2+c,
y3=ax32+bx3+c,как
правило,не буду удовлетрорят ур-ям:
y4=ax42+bx4+c…,
yn=axn2+bxn+c,если
у(х) не явл. Квадратичным
трехчленом.по-другому,zk-yk=ɛk(k=1,2…n),где
ɛk-погрешности.параметры
а,в,с выберем так,чтоб сумма квадратов
уклонений:u=
ɛ12+
ɛ22+…+
ɛn2=(z1-y1)2+(z2-y2)2+…=(
ax12+bx1+c-y1)2+(
ax22+bx2+c-y2)2+(
axn2+bxn+c-yn)2
была наим.нужно,чтоб
|
23Признак Коши и Даламбера. Сходимость рядов. Признак
Даламбера.
Будем
считать, что все
Док-во:
1случай.
Пусть
.
Из того, что сущ-т выписанный предел
следует, что 24.Признак
Коши. Пусть
в р1
Сущ. и до. признаки сходимости рядов. Лейбниц:если модули членов знакочередующегося ряда монотонно не убывают при >их номера,а общий член→0,то этот ряд-сходящийся. 26. Дифференциал. Уравнение с разделяющимися переменными. Его применение в химии. ур-я,
в кот.входят производные или
дифференциал,наз.дифференциальными.
дифф.ур-ем 1ого порядка наз.ур-е,связывающее
независимую переменную,искомую
функцией этой пер-ой и ее производную.если
y=y(x)-фун-я
независ. пер. х,то в общем виде:
F(x,y,y`)=0.если
уравнение разрешимо относительно
y`,то
Диф.
Ур-е 1-го пордка с разделяющимися
переменными наз.ур-е вида:
X(x)Y(y)dx+X1(x)Y1(y)dy=0
(1),где Х и Х1-фун-и только от х,Y
и Y1-только
от y
если X1(x)Y(y)
не равно 0, разделив обе части ур-я
(1)на это произведение,получим: 9. приближенное вычисл. определ.интегралов 1)Пусть
требуется найти определенный интегралот
непрерывной функции ƒ(х). Если можно
найти первообразную
Ньютона-Лейбница:
2)
ф-а прямоугольников. Пусть на отр.[a,b]
(a<b)
задана непрерывная функция ƒ(х).
Требуется вычислить интеграл численно
равный площади соотв. кривол. трапеции.
Разобьем основание трапеции на n
частей длины n=(b-a)/n=xi-x(i-1)(шаг
разбиения). В серед. ci=(x(i-1)-xi)/2каждого
отр. строим ординату yi=f(ci)графика
ф-иy=f(x).
построим прямоугольник с S=hy
i.
Тогда сумма
площадей всех n прямо угольников дает
площадь ступенчатой фигуры, представляющую
собой приближенное значение искомого
определенного интеграла.
35. Элементы комбинаторики. Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой.Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать k способами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами. Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться). Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно .mk Размещение
без повторений.
Из множества, содержащего m различных
элементов, надо выбрать упорядоченное
подмножество из k элементов (k£m), то
есть такое подмножество, в котором
элементы располагаются в определенном
порядке, и изменение порядка элементов
изменяет подмножество. Кроме этого,
элементы в выбранном подмножестве не
повторяются. Требуется выяснить,
сколько таких комбинаций существует.
По правилу произведения получаем, что
первый элемент можно выбрать m способами,
второй элемент – (m-1) способом, и так
далее, а элемент с номером k можно
выбрать (m – k + 1) способами. Следовательно,
число упорядоченных k-элементных
подмножеств, взятых из множества,
содержащего m элементов равно
m(m-1)(m-2)…(m-k+1). Такие подмножества
называются размещениями из m элементов
по k элементов, а их общее число можно
выразить формулой . Перестановки. Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно: Pm=m(m-1)(m-2)…3*2*1=m! Сочетания.
Пусть из множества, содержащего m
различных элементов, требуется выбрать
подмножество, содержащее k различных
элементов (k £ m). Получаемые при этом
подмножества не упорядочены. Такие
неупорядоченные подмножества называются
сочетаниями. Число сочетаний из m
элементов по k элементов вычисляется
по формуле:
|
28.Радиус и интервал сходимости степенного ряда.
31. Формулы Эйлера. Степенной
ряд(1) с комплексными членами: 28. Дифференциальное уравнение Бернулли. . Зная,что
43. Схема Бернулли. Найвероятнейшее число осуществлений события. рассм.среднюю однотипичных независимых испытаний,в каждом из кот. Событие А может осущ. С заданной Р или не осущ. с q.т.к. А и А`-противоположны,то р+q=1→q=1-р.если в задаче требуется найти Р того,что в серии их n испытаний А осущ.К раз,то данные последовательности испытаний наз: Рn(K)→схемами Бернулли.Pn(K)=Cnkpkqn-k(где А=К,А`=n-K).вероятность угадать 5 из 36:Р365=… Рn(m)=Cnmpmqn-m.где
Р(m1≤m≤m2),если
m1,m+1…m2-несовместное
событие→ Р(m1≤m≤m2)=Pn(m1)+Pn(m+1)+…+Р(m2);
(n-m\m+1)*p\q>1; np-mp>mq+q; np-q>m(p+q); m<np-q-фун-я при таких n –возрастающая.значит m>np-q-фун-я убывающая.→сущ-ет точка экстремума.докажем,что экстремум,т.е. m-целое число.пусть искомая точка –m0,тогда Рn(m0)≥Рn(m0-1)/аналогично Рn(m0)≤Pn(m0-1).решим систему 2х неравенств:n(n-1)…(n-m0+1)\m0!)*pm0qn-m0≥n(n-1)…((n-(m0-1)+1)\(m0-1)!)*pm0-1qn-m0+1; p(n-m0+1)≥qm0; pm-pm0-qm0+p≥0; m0≤p(n-1).аналогично рассм.2е неравенство получ.:m0≥(n-1)q 44. Формула Пуассона. пусть
n-большое
число,р>0,но очень мало,тогда исходя
из формулы Бернулли Pn(K)=Cnkpkqn-k,введем
λ=np-число
средней величины,тогда р=λ\n.
|
20. Интегралы по периоду от основных тригонометрических функций. Тригоном.ряд: Лемма:1) 2)
квадрата
любой ф-и≠0,причем
21. Ряд Фурье. Пусть
задана система ортогональных на
27. Линейное дифференциальное уравнение первого порядка. ур.-е
30. Структура общего решения линейного неоднородного уравнения второго порядка. Линейное
неоднородное уравнение имеет вид
29. Линейное однородное дифференциальное уравнение второго порядка. Структура общего решения.
F(x,y,y`,y``)=0-ур-е 2го порядка.если y``=1,y`=x+C1,y=x2\2+C1x+C2-(cемейство ф-ций,зависящих от С1 и С2)-общим решение ур-я 2-го порядка наз. Семейство ф-й y=ⱷ(x,C1,C2),-где х-независ.переменная.С1,С2-произвольные постоянные.причем их кол-во нельзя уменьшить путем их непрерывной замены.решить задачу Коши,значит из общего решения зад.Коши выделить то,кот.удволетворяет для: у(х0)=у0;у`(х0)=у0`.где у и у`,х0-заданные фиксированные числа.это частно решение.могут сущ-ть реш.,кот.не содержатся в общем реш.,они наз.-особыми решениями:у``+а(х)y`+b(x)y=f(x),где а(х),b(х)-непрерывные ф-ии,-лин.диф.ур-е 2го порядка.общего случая решения нет.,если ур-е имеет вид у``+а(х)y`+b(x)y=0,то это лин.однородное ур-е 2го порядка. Пусть y1(x) и у2(х)-решения ур-я,тогда их линейная комбинация: у=С1у1(х)+С2у2(х),также реш.ур-я.проверка: 31. Линейное однородное уравнение второго порядка с постоянными коэффициентами. Случай различных корней характеристического уравнения. у``+py`+qy=0(1),где р и q-вещественные чсила=const-однородное диф.ур-е с постоянные коэффиц.общее решение-комбинация частных независимых решений,значит: y=ekx,k2exk+pk ekx +q ekx =0,разделим на ekx(ekxне равно 0),получим определяющее ур-е:k2+pk+q=0 Если D=p2\4+q>0,то ур-е имеет два корня.тогда y1=ek1x,y2=ek2x-решения ур-я(1).причем решения линейно не зависимы.об-е реш. у``+а(х)y`+b(x)y=0 будет y=C1 ek1x+C2 ek2x 32 Линейное однородное уравнение второго порядка с постоянным коэффициентом. Случай кратных корней характеристического уравнения. у``+py`+qy=0(1),где р и q-вещественные числа=const-однородное диф.ур-е с постоянные коэффиц.общее решение-комбинация частных независимых решений,значит: y=ekx,k2exk+pk ekx +q ekx =0,разделим на ekx(ekxне равно 0),получим определяющее ур-е:k2+pk+q=0 если D=0.то должны существовать x1,2=-p\2,то y1,2=е-р\2*х,то у1(х)/у2(х)=z(x).т.к. решения должны быть линейно не завис. У1(х)=у2(х)z(x); y1`=z`y2+zy2`; y1``=z``y2+2z`y2`+zy2``.подставляя в у``+py`+qy=0,получ.z=ax+b,b=0,a=1,z=x,y2=xe-p\2*x.решим y``+2y`+y=0.к1=к2=-1.общее решение y1=ekx=e-p\2*x;y=C1e-x+C2xe-x 33 Линейное однородное уравнение второго порядка с постоянным коэффициентом. Случай комплексных корней характеристического уравнения. у``+py`+qy=0(1),где р и q-вещественные чсила=const-однородное диф.ур-е с постоянные коэффиц.общее решение-комбинация частных независимых решений,значит: y=ekx,k2exk+pk ekx +q ekx =0,разделим на ekx(ekxне равно 0),получим определяющее ур-е:k2+pk+q=0. если D<0,то k1,2=a±bi,тогда y1=eaxcosbx; y2=eaxsinbx. Общее решение y=eax(C1cosbx+C2sinbx).для решения ур-я у``+py`+qy=0 коэффиц. Должны быть =.в противном случае ур-е не имеет реш.
|
4.Вычисление длины дуги и объема тела.
Гладкая кривая – имеет непрерывно от точки к точке меняющуюся касательную (имеет непрерывную производную. Периметр ломанной М0 – Мn при достаточно больших n и достаточно маленьких Мi-1Mi примерно равен длине дуги.
П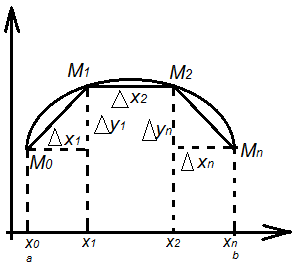 о
определению, за длину дуги l
принимается
о
определению, за длину дуги l
принимается

x0 = a
xn = b
Сделаем разбиение отрезка ab:
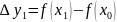


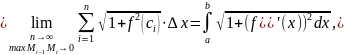

Формула вычисления объема тела
Пусть в каждой точке х есть S поперечного сечения, тогда V тела, ограниченного двумя близкими областями, расположенными на расстоянии х, V цилиндра с высотой n=x, и Sосн=S(ci), где сi[x; x+x]
Объем тела
В частности, если тело получено вращением криволинейной трапеции, ограниченной сверху кривой , то S каждого сечения
.
6. Частная производная и дифференциал функции нескольких переменных.
Частная производная
функции по аргументу х – предел отношения
частного приращения ф-ции по этому
аргументу к приращению аргумента, при
стремлении последнего к нулю:
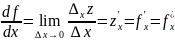 ,
,
 .
Изменяется только одна из переменных.
Поэтому при вычислении производных
«постоянную» переменную можно считать
постоянной.
.
Изменяется только одна из переменных.
Поэтому при вычислении производных
«постоянную» переменную можно считать
постоянной.
Пример:

Дифференцируемая функция:
Если полное приращение ф-ции, т.е. величина , представимо в виде: (где А и В не зависят от и ,О – величина бесконечно малая более высокого порядка, чем её аргумент, при стремлении аргумента к нулю), то функция назыв. дифференцируемой в т. X(x,y), а .(1)
Положив в равенстве 1 , разделив на обе части равенства и перейдя к пределу, получили, что , аналогично →найдя диф.фун-и z=x, получ. dx=∆x и dy=∆y→dz=
7.Экстремум функции нескольких переменных.
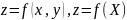
Точка (x0,y0)
назыв. точкой максимума ф-ции z,
если существует такая окрестность этой
точки, что для всех точек с коорд. (х,у)
из этой окрестности
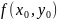 >
> Точка
Точка
 назыв. точкой мин. ф-ции z,
если сущ. окрестность что
назыв. точкой мин. ф-ции z,
если сущ. окрестность что
 для
всех точек окрестности.
для
всех точек окрестности.
Т. (x0,y0)
назыв. точкой экстремума, а знач.
ф-ции в этой точке – макс. и мин.,
собирательно экстремумом. Если т.
явл. экстремумом ф-ции, то она явл.
экстремумом по каждой из переменных.
Из необход.усл.экстр.ф-ции переменной
следует, что необх.усл.экстр.ф-ции 2х
переменных, явл.равенство нулю частных
производных этой ф-ции.( ,
если эти производные существуют.
Существуют
и достаточные условия экстремума функции
2-х переменных.
,
если эти производные существуют.
Существуют
и достаточные условия экстремума функции
2-х переменных.
10.Производная от сложной фун-и.
Сущ.т:
 .
Можно док-ть,что это производные =. Пусть
х=х(t),y=y(t),посчитаем
z=f(x,y)т.е.z=f(x(t),y(t))=F(t).док-м,что
производная сложной ф-ии сущ-т и
вычисляется по
формуле:F`(t)=f`x(x(t).y(t))xt`+fy`(x(t),y(t))yt`.или:
.
Можно док-ть,что это производные =. Пусть
х=х(t),y=y(t),посчитаем
z=f(x,y)т.е.z=f(x(t),y(t))=F(t).док-м,что
производная сложной ф-ии сущ-т и
вычисляется по
формуле:F`(t)=f`x(x(t).y(t))xt`+fy`(x(t),y(t))yt`.или: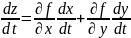 .
для этого найдем полное приращение
фун-и:
.
для этого найдем полное приращение
фун-и: .разделим
на ∆t каждый член и перейдем
к lim при ∆t→0,получим:F`(t)=
.разделим
на ∆t каждый член и перейдем
к lim при ∆t→0,получим:F`(t)=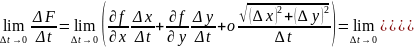
Если задана ф-я 2х переменных z=f(x,y),то модно сказать,что задано скалярное поле,т.е. каждой точке плоскости соотв.к.-то число. Если каждой точке пл соотв. вектор,то задано векторное поле.
12. Арифметика числовых рядов.
Выражение
 ,
где
,
где
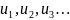 числа, формально соед. между собой «+».
Назовем это выр-ние числовым рядом (
числа, формально соед. между собой «+».
Назовем это выр-ние числовым рядом ( ).
Сумма
).
Сумма
 называется частичной суммой ряда. Если
сущ. конечный предел
называется частичной суммой ряда. Если
сущ. конечный предел
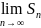 ,
то он называется суммой ряда, а ряд
сходящимся. (обознач. S).
,
то он называется суммой ряда, а ряд
сходящимся. (обознач. S).
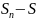 - остаток ряда.
- остаток ряда.
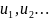 -
члены ряда.
-
общий член ряда. Обозначим остаток ряда
-
члены ряда.
-
общий член ряда. Обозначим остаток ряда
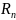 .
.
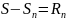 ;
;
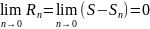 .
Рассмотрим геом.прогр.:
.
Рассмотрим геом.прогр.:
 .
.
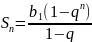 .
Если |q|< 1:
.
Если |q|< 1:
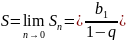 – ряд сходится. Если
– ряд сходится. Если
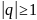 ,
то ряд расх.
,
то ряд расх.
Теорема1.
Сходимость числового ряда не наруш.,
если все его члены умножить на 1 и тоже
число(не 0). Т.е. если сходится ряд
 и наоборот.
и наоборот.
Док-во.
Рассмотрим частичные суммы:
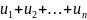 ;
;
 .
Ясно, что если имеет предел 1-ое из послед.
част. сумм, то имеет предел и вторая.
И наоборот.переходя к lim,
Получим требуемое, ч.т.д.
.
Ясно, что если имеет предел 1-ое из послед.
част. сумм, то имеет предел и вторая.
И наоборот.переходя к lim,
Получим требуемое, ч.т.д.
Теорема2.
Алгебр. сумма двух сходящ.
рядов – сход.ряд: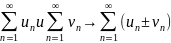 .
Действительно для последнего ряда
.
Действительно для последнего ряда


 .
.
 пределённый
интеграл
пределённый
интеграл
 численно равен площади фигуры,
ограниченной осью абсцисс, прямыми x
= a и x = b и графиком функции f(x).
численно равен площади фигуры,
ограниченной осью абсцисс, прямыми x
= a и x = b и графиком функции f(x). ,
где х, t – любые буквы.
,
где х, t – любые буквы.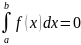

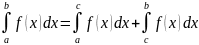 (адитивность)
(адитивность)
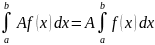
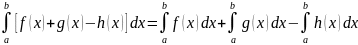
 ,
представимо в виде:
,
представимо в виде:
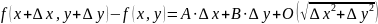 (где А и В не зависят от
(где А и В не зависят от
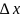 и
и
 ,О
– величина бесконечно малая более
высокого порядка, чем её аргумент, при
стремлении аргумента к нулю), то функция
назыв. дифференцируемой в т. X(x,y),
а
,О
– величина бесконечно малая более
высокого порядка, чем её аргумент, при
стремлении аргумента к нулю), то функция
назыв. дифференцируемой в т. X(x,y),
а
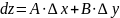 .(1)
.(1) ,
разделив на
обе части равенства и перейдя к пределу,
получили, что
,
разделив на
обе части равенства и перейдя к пределу,
получили, что
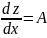 ,
аналогично
,
аналогично
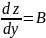 →найдя
диф.фун-и z=x,
получ. dx=∆x
и dy=∆y→dz=
→найдя
диф.фун-и z=x,
получ. dx=∆x
и dy=∆y→dz=
 .
Док-во: т.к. f(x)
непрерывна на [a,b],
то она достигает своего макс и мин
значения на этом отрезке. Значит М>=
f(x)>=m.
Отсюда: m(b-a)<=
.
Док-во: т.к. f(x)
непрерывна на [a,b],
то она достигает своего макс и мин
значения на этом отрезке. Значит М>=
f(x)>=m.
Отсюда: m(b-a)<=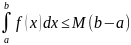

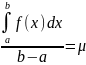 Откуда и следует теорема о среднем.
Откуда и следует теорема о среднем.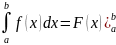 =F(b)-F(a)
=F(b)-F(a) Если:1.Ф-я x=
Если:1.Ф-я x=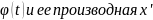 =
=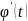 непрерывны при t
на [a,b]
непрерывны при t
на [a,b]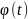 при t
на [a,b]
явл. отрезок [a,b].
3.
при t
на [a,b]
явл. отрезок [a,b].
3.
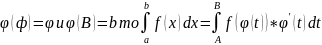 .
.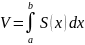
 частности, если тело получено вращением
криволинейной трапеции, ограниченной
сверху кривой
частности, если тело получено вращением
криволинейной трапеции, ограниченной
сверху кривой
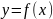 ,
то S
каждого сечения
,
то S
каждого сечения
 .
.

 ,
если он существует.
,
если он существует.
 сходятся и расходятся одновременно,если
одна из величин→к∞,то и др.тоже. (
сходятся и расходятся одновременно,если
одна из величин→к∞,то и др.тоже. (

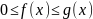 ,
то из сходимости
,
то из сходимости
 следует сходимость интеграла
следует сходимость интеграла
 .
.
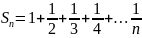 . Гармонический
ряд является исторически первым
примером численного ряда, члены
которого неограниченно убывают и
который, несмотря на это, расходится,
т.е. для которого
. Гармонический
ряд является исторически первым
примером численного ряда, члены
которого неограниченно убывают и
который, несмотря на это, расходится,
т.е. для которого 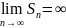 .
.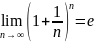 ,
где
подпредельная функция монотонно
возрастает, то
,
где
подпредельная функция монотонно
возрастает, то  ,
где e=2.718.... Возьмем от обеих частей
неравенства натуральный логарифм:
,
где e=2.718.... Возьмем от обеих частей
неравенства натуральный логарифм:  .
Или
.
Или
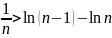 .
При n = 1,2,3, ... n последовательно получим:
.
При n = 1,2,3, ... n последовательно получим:
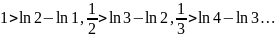
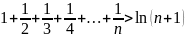 или
или
 Если
количество членов ряда неограниченно
растет, то неравенство показывает,
что сумма гармонического ряда
неограниченно растет, т.е.
Если
количество членов ряда неограниченно
растет, то неравенство показывает,
что сумма гармонического ряда
неограниченно растет, т.е. 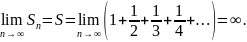
 сходится, то сх-ся и ряд1.
сходится, то сх-ся и ряд1.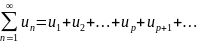 приэтом
ряд(6)сод-т абсолютные величины.
приэтом
ряд(6)сод-т абсолютные величины.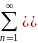 т.к.
0≤u1+|u1|≤2|u1|…0≤un+|un|≤2|un|
из сходимости ряда (6) следует
сход.
т.к.
0≤u1+|u1|≤2|u1|…0≤un+|un|≤2|un|
из сходимости ряда (6) следует
сход.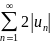 →сходится
ряд
→сходится
ряд ,т.к.
все его члены<. Если
=S,то
,т.к.
все его члены<. Если
=S,то

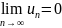 ,
,
 – общий член. (обратное утв. не верно)
– общий член. (обратное утв. не верно) и
и
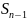 .
.
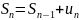 .
.
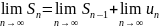

 ;
.
;
.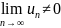 ,
то ряд расходится.
,
то ряд расходится. .
.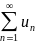 отбросить конечное число 1х членов,
то сходимость/расходимость не нарушится.
отбросить конечное число 1х членов,
то сходимость/расходимость не нарушится.
 ,
,
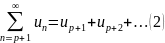
 .
Пусть
.
Пусть
 ,
,
 - частичная сумма ряда 2.
- частичная сумма ряда 2.
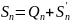 .
Если ряд 1 сходится, то
.
Если ряд 1 сходится, то
 ,
,
 .
Следует, что существует
.
Следует, что существует
 ,
значит, ряд 2 сходится, ч.т.д. Если ряд
1 расходится, то
,
значит, ряд 2 сходится, ч.т.д. Если ряд
1 расходится, то
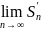 не существует, а ряд 2 тоже расходится.
не существует, а ряд 2 тоже расходится.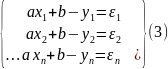 ,где
,где
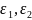 -уклонения,или
погрешности.
-уклонения,или
погрешности.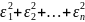 (4),была
наим.подставим (3) в
(4),получ.:u=(ax1+b-y1)2+(ax2+b-y2)2+…+(axn+b-yn)2.переменная
u
явл. Фун-й перменных а и в .подберем
параметры а и в так,чтоб u
принимала возможно меньшее знач.→
(4),была
наим.подставим (3) в
(4),получ.:u=(ax1+b-y1)2+(ax2+b-y2)2+…+(axn+b-yn)2.переменная
u
явл. Фун-й перменных а и в .подберем
параметры а и в так,чтоб u
принимала возможно меньшее знач.→ .находя
частные производные фун-и u
по а и в,приравнивая их к 0,получ.
нормальную сист.ур-й:
.находя
частные производные фун-и u
по а и в,приравнивая их к 0,получ.
нормальную сист.ур-й: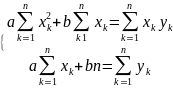 ,из кот. Опред.
Параметры а и в эмпирической ф-лы (1)
,из кот. Опред.
Параметры а и в эмпирической ф-лы (1)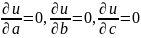 .находя производные ф-и u(а,в,с)по
переменным а,в,с и приравнивая их
к0,получаем нормальную сист. Ур-й:
.находя производные ф-и u(а,в,с)по
переменным а,в,с и приравнивая их
к0,получаем нормальную сист. Ур-й: ,
из кот.опред.знач. параметров эмпирической
формулы (1)
,
из кот.опред.знач. параметров эмпирической
формулы (1)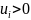 в ряду
.
Пусть существует
в ряду
.
Пусть существует
 .
Тогда если
.
Тогда если
 ,
то ряд1 сходится. Если
,
то ряд1 сходится. Если
 – расходится. Если
– расходится. Если
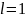 – доп.ислед.
– доп.ислед. ,
такой, что
,
такой, что
 выполняется нер-во:
выполняется нер-во:
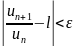 .
Для таких n:
.
Для таких n:
 .
Выберем
.
Выберем
 достаточно маленьким, так, чтобы
величина
достаточно маленьким, так, чтобы
величина
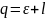 <1. Тогда
<1. Тогда
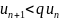 ,
для n>N
(n=N+1,
N+2…),
значит uN+2<quN+1,
uN+3<quN+2<q2uN+1
и т.д. Получим, что ряд
,
для n>N
(n=N+1,
N+2…),
значит uN+2<quN+1,
uN+3<quN+2<q2uN+1
и т.д. Получим, что ряд
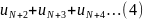 получен из ряда1 путем отбрасывания
1х uN+1
членов. Если он сходится, то, по док-му,
сходится и ряд1. Но все члены этого
ряда4 не превосх. членов ряда
получен из ряда1 путем отбрасывания
1х uN+1
членов. Если он сходится, то, по док-му,
сходится и ряд1. Но все члены этого
ряда4 не превосх. членов ряда
 ,
кот.явл. суммой геом.прогр. с знаменателем
меньше 1. Т.к. ряд5 сход-ся, то сх-ся и
ряд4, и 1. 2случай.
.
Все так же, только
,
кот.явл. суммой геом.прогр. с знаменателем
меньше 1. Т.к. ряд5 сход-ся, то сх-ся и
ряд4, и 1. 2случай.
.
Все так же, только
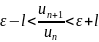 ,
,
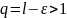 ,
то
,
то
 ;
;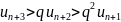 ;
;
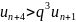 .
Начиная с N+2,
все члены р4 > членов р5. Т.к. р5 расх-ся,
то расх-ся и р4, р1., ч.т.д.
.
Начиная с N+2,
все члены р4 > членов р5. Т.к. р5 расх-ся,
то расх-ся и р4, р1., ч.т.д. .
При
ряд сходится, при
расх-ся,
доп.исслед.lдок-о
аналогично док-ву Даламбера.
.
При
ряд сходится, при
расх-ся,
доп.исслед.lдок-о
аналогично док-ву Даламбера.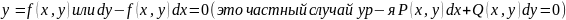
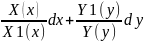 =0-ур-е
с разделенными переменными :при dx
фун-я только от х,при dy-только
от у.если взять инт.от обеих частей:
=0-ур-е
с разделенными переменными :при dx
фун-я только от х,при dy-только
от у.если взять инт.от обеих частей: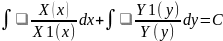 ,в
данной сумме равенством выражается
общий инт.ур-я(1),решением ур-я (1) явл.
Корни: X1(x)=0,Y(y)=0
,в
данной сумме равенством выражается
общий инт.ур-я(1),решением ур-я (1) явл.
Корни: X1(x)=0,Y(y)=0

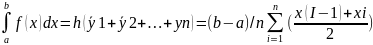


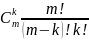
 .
Исслед-ие сх-ти степенного ряда сводится
к исс-ию сх-ти числового ряда, где
.
Исслед-ие сх-ти степенного ряда сводится
к исс-ию сх-ти числового ряда, где
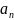 – числовые коэф-ты,
– числовые коэф-ты,
 – заданное число. Рассмотрим более
простой ряд:
– заданное число. Рассмотрим более
простой ряд:

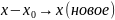 .
Метод Даламбера:
.
Метод Даламбера:
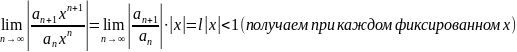 ,
если
,
если
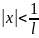 ,
ряд сходится в интервале
,
ряд сходится в интервале
 – интервал сходимости
ряда. Если
обозначить
– интервал сходимости
ряда. Если
обозначить
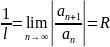 ,
то ряд1 сх-ся на интервале (-R;R)
– радиус
сходимости.
,
то ряд1 сх-ся на интервале (-R;R)
– радиус
сходимости.
 .
.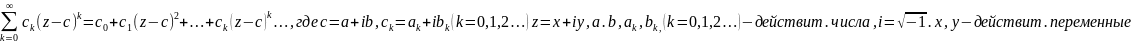 .если
с=0,то
.если
с=0,то
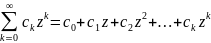 .ряд(1)сводится
к степенному,при введении новой пер.
Z=z-c.для
комплексной пер.Z
можно опред-ь f
ez
посредством формулы:
.ряд(1)сводится
к степенному,при введении новой пер.
Z=z-c.для
комплексной пер.Z
можно опред-ь f
ez
посредством формулы: Док-ть,что
ряд сходится при любом z
можно по принципу Даламбера,если
z=x,то
Док-ть,что
ряд сходится при любом z
можно по принципу Даламбера,если
z=x,то

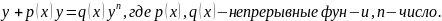 -общее
ур-е бернулли.решается с помощью замены
y(x)=u(x)v(x),аналогично
М(x,y)dx+N(x,y)Dy=0.полный
диф.некот.фун-и,т.е.du=M(x,y)dx+N(x,y)dy,тогда
общее решение u(x,y)=C.значит,условие,при
кот.сущ-т такая фун-я u
-общее
ур-е бернулли.решается с помощью замены
y(x)=u(x)v(x),аналогично
М(x,y)dx+N(x,y)Dy=0.полный
диф.некот.фун-и,т.е.du=M(x,y)dx+N(x,y)dy,тогда
общее решение u(x,y)=C.значит,условие,при
кот.сущ-т такая фун-я u +
+ .если
частные производные непрерывны,то их
смешанные производные=.
.если
частные производные непрерывны,то их
смешанные производные=.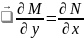 ,тогда
ур-е будет в полных дифференциалах.тогда
u(x,y)=C.
Пример:(х2-ay)dx+(y2-ax)dy=0,где
a=const.решая,получ.
u(x,y)=(x3\3)-ayx+(y3\3);общее
решение: (x3\3)-ayx+(y3\3)=C;
,тогда
ур-е будет в полных дифференциалах.тогда
u(x,y)=C.
Пример:(х2-ay)dx+(y2-ax)dy=0,где
a=const.решая,получ.
u(x,y)=(x3\3)-ayx+(y3\3);общее
решение: (x3\3)-ayx+(y3\3)=C; =(n(n-1)*…*n-m-1+1\(m+1)!)\(n(n-1)+…+(n-m+1)\m!)*p\q=…(n-m\m+1)*p\q
=(n(n-1)*…*n-m-1+1\(m+1)!)\(n(n-1)+…+(n-m+1)\m!)*p\q=…(n-m\m+1)*p\q -формула
Пуассона(распределение Пуассона),где
λ=np-параметр
распределения.(в таблице а=λ)
-формула
Пуассона(распределение Пуассона),где
λ=np-параметр
распределения.(в таблице а=λ)
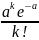
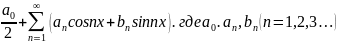 -действит.числа,коэф-ы
ряда.тригоном.сист.ф-й наз.мно-во
ф-й:1,cosx,sinx,cos2x,sin2x…cosnx,sinnx.
-действит.числа,коэф-ы
ряда.тригоном.сист.ф-й наз.мно-во
ф-й:1,cosx,sinx,cos2x,sin2x…cosnx,sinnx. от
произведения любых 2х различ.ф-й=0:
от
произведения любых 2х различ.ф-й=0: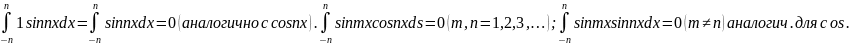 док-о:
док-о:
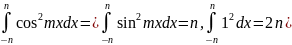 Док.во:
Док.во:
 функций
функций
 и на промежутке
и на промежутке
 ф-ция f(x).
Тогда ф-цию можно представить в виде
ряда Фурье:
ф-ция f(x).
Тогда ф-цию можно представить в виде
ряда Фурье:
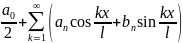 ,
где коэфициенты ряда
,
где коэфициенты ряда

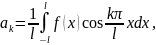
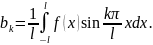 Если на
f(x)
неч., то
Если на
f(x)
неч., то
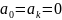 :
:
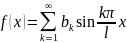 ,
где
Если
,
где
Если
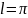 то ряд Фурье прин. вид
то ряд Фурье прин. вид
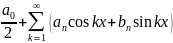 ,
где
,
где


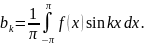
 -(где
р(х) и q(x)-непрерывные
фун-и своего аргумента),лин.диф.ур-е1-го
порядка. Его решение ищут в виде
произведения 2-х фун-й:y(x)=u(x)v(x),где
u,v-новые
функции .подставляем в ур-е
-(где
р(х) и q(x)-непрерывные
фун-и своего аргумента),лин.диф.ур-е1-го
порядка. Его решение ищут в виде
произведения 2-х фун-й:y(x)=u(x)v(x),где
u,v-новые
функции .подставляем в ур-е ,выр.
В ()должно=0,тогда:получаем
,выр.
В ()должно=0,тогда:получаем
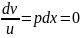 .интегрируя,получ.:
.интегрируя,получ.: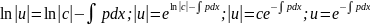 подставляем.и
находим
подставляем.и
находим
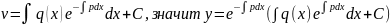
 ,
где коэф-ты
,
где коэф-ты
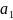 и
и
 и неоднородность f
неприрывны на I,
или в оперативной форме
и неоднородность f
неприрывны на I,
или в оперативной форме
 .
Предположим, что для ур-ния1 известно
частное решение
.
Предположим, что для ур-ния1 известно
частное решение
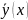 ,
т.е.
,
т.е.
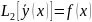 .
Введем новую неизвестную ф-цию z
по формуле
.
Введем новую неизвестную ф-цию z
по формуле
 .
Подставляя ф-цию3 в уравнение2, получаем:
.
Подставляя ф-цию3 в уравнение2, получаем:
 или
или
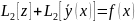 .
Значит,
.
Значит,
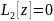 ,
или
,
или
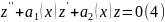 ,
это однородное линейное уравнение,
соотв=щее неоднородному ур-нию1. Общее
решение однор.ур-ния зад.формулой:
,
это однородное линейное уравнение,
соотв=щее неоднородному ур-нию1. Общее
решение однор.ур-ния зад.формулой:
 ,
где
,
где
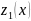 и
и
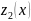 - линейно независимые частные решения
ур-ния4. Подставляя значение z
в формулу3, получаем все решения
уравнения1:
- линейно независимые частные решения
ур-ния4. Подставляя значение z
в формулу3, получаем все решения
уравнения1:
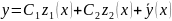 .
– общее решение неоднородного ур-ния1.
.
– общее решение неоднородного ур-ния1.