17) Резонанс в последовательном контуре. Условия резонанса

УСЛОВИЯ: Если частота колебаний генератора совпадает с частотой свободных колебаний в контурах, реактивные сопративления XL (Катушка индуктивности) и XC (конденсатор) равны между собой, тогда напряжение на катушке и конденсаторе равны и в Q раз больше Uвых.

Колебания происходят в ходе подключения источника энергии (UL= I*X), (UC= I*Xc).

РЕЗОНАНС ТОКОВ: Явление в парралельном контуре, когда частота при резонансе Fо равна реактивному сопративлению Z между собой и волновому Zо ,токи равны на этих участках и в Q раз больше чем ток в неразвлетвленном участке цепи.

20)Понятие резонанса в параллельном контуре.

Источник подключается к колебательному контуру , чтобы компенсировать энергетических потери.

X_L=2ПfL Х_С=1/2ПFс f=f_СВ=>X_L0=X_С0 I_C0=

На частоте f₀(резонансная частота) равны реактивные сопративления=> равны токи на участке с реактивными сопративлениями.

Резонанс токов -явление в параллельном контуре, когда f₀ равны реактивные сопротивления X_L0=X_C=q = волновому сопротивлению , следует что равны токи на этих участках и в Q раз больше чем ток в неразветленной части цепи.

21)Последовательный колебательный контур. Зависимость сопротивлений контура от частоты.

Последовательный колебательный контур является простейшей резонансной (колебательной) цепью. Состоит последовательный колебательный контур, из последовательно включенных катушки индуктивности и конденсатора. При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина которого вычисляется по закону Ома: I = U / Х_Σ , где Х_Σ - сумма реактивных сопротивлений последовательно включенных катушки и конденсатора (используется модуль суммы)

22)Вынужденные колебания в параллельном rlc– контуре.

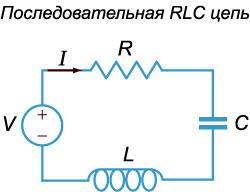
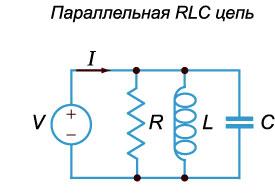
В электрической цепи, содержащей сопротивление R, индуктивность L и емкость C, могут возбуждаться электрические колебания. С точки зрения топологии чаще всего рассматриваются два вида электрических цепей: последовательная RLC-цепь (рисунок 1) и параллельная RLC-цепь (рисунок 2).

Рис.1		Рис.2

Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1):

e (t) = 0 cos ωt,

где ₀ – амплитуда, ω – круговая частота.

Рисунок 2.3.1. Вынужденные колебания в контуре

Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарност. Поэтому для мгновенных значений токов и напряжений можно записать закон Ома:

Величина – это ЭДС самоиндукции катушки, перенесенная с изменением знака из правой части уравнения в левую. Эту величину принято называть напряжением на катушке индуктивности.

Уравнение вынужденных колебаний можно записать в виде

uR + uC + uL = e (t) = 0 cos ωt,

где u_R (t), u_C (t) и u_L (t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U_R, U_C и U_L. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока. Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм.

Теперь рассмотрим параллельную RLC-цепь и выведем для нее аналогичное дифференциальное уравнение.

По первому закону Кирхгофа полный ток будет равен сумме токов через сопротивление R, катушку индуктивности L и конденсатор C (рисунок 2):

Учитывая, что

для случая постоянного полного тока I(t) = I₀ получаем следующее дифференциальное уравнение 2-го порядка относительно переменной V:

Как видно, мы снова п-риходим к уравнению, описывающему затухающие колебания. Таким образом, колебательный режим может возникать и в параллельных RLC-цепях.