14)Идеальный колебательный контур. Свободные колебания в контуре.

Идеальный колебательный контур

Колебательный контур называется идеальным, если он состоит из катушки и емкости и в нем нет сопротивления потерь.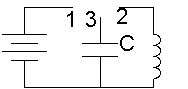

Краткая теория

Колебательный контур состоит из катушки индуктивностью L и конденсатора емкостью C. В идеальном колебательном контуре активное сопротивление R = 0.

Колебательный контур – колебательная система. В контуре происходят периодические изменения энергии электрического поля конденсатора и магнитного поля тока катушки.

В любой момент времени полная энергия при R = 0:

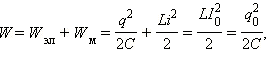
где q и i – мгновенное значение, а q₀ и I₀ – амплитудные значения.

Свободные электрические колебания в идеальном колебательном контуре являются гармоническими.

Заряд на конденсаторе изменяется по закону:

q = q0cosω0t.

Учитывая, что U = q / C, можно также получить уравнение для изменения напряжения на конденсаторе:

u = U0 cosω0t.

Ток в катушке индуктивности:

i = I0 cos (ω0t+π/2),

или

i = I0 sinω0t.

Период свободных колебаний определяется параметрами самой колебательной системы: индуктивностью и емкостью (формула Томсона):

Определим угловую частоту свободных колебаний:

Используем равенство энергий электрического и магнитного полей

где ώ угловая частота свободных колебаний.

[ ώ ]=1/с

f0=ώ/2π [Гц].

Период свободных колебаний Т0=1/f.

Частоту свободных колебаний называют частотой собственных колебаний контура.

Из выражения: ώІLC=1 получим

ώL=1/Cώ , следовательно, при токе в контуре с частотой свободных колебаний индуктивное сопротивление равно емкостному сопротивлению.

-характеристические сопротивления.

Индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний называется характеристическим сопротивлением.

15)Вынужденные колебания в последовательном колебательном контуре. Пояснить процессы протекающие в контуре.

Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодиче­ски изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную ЭДС (рис. 8.6), изменяющуюся во времени по гармоническому закону с частотой

При частоте вынуждающей ЭДС, меньшей частоты собственных колебаний, реактивное со­

противление контура имеет емкостной характер, при этом колебания силы тока опережают по

фазе колебания вынуждающей ЭДС. При частоте вынуждающей ЭДС, большей частоты собствен­ ных колебаний, реактивное сопротивление контура имеет индуктивный характер, при этом коле­ бания силы тока отстают по фазе от колебаний вынуждающей ЭДС.

16)Вынужденные колебания в параллельном колебательном контуре.

В радиотехнических устройствах особенно часто встречаются цепи, в которых элементы колебательного контура (катушка и конденсатор) при подключении к источнику э.д.с. соединяются параллельно . Такой контур называется параллельным.

Частота вынужденных колебаний совершенно не зависит от параметров колебательного контура; она всегда равна частоте источника, подключенного к контуру. Ток в цепи создается источником, и на какую бы частоту ни был настроен колебательный контур, ток будет изменяться с такой частотой, какую имеет источник. Этим вынужденные колебания существенно отличаются от свободных колебаний , частота которых зависит от параметров контура.

Параллельный контур характеризуют полосой пропускания, в пределах которой общий ток в цепи источника увеличивается не более чем в раз по сравнению с током при резонансной частоте.