31. Понятие о законах распределения случайных величин. Закон нормального распределения

Теоретические законы распределения случайных величин

Конкретный вид функции распределения случайных величин зависит от конкретно решаемой задачи. По результатам экспериментов и наблюдений могут быть построены гистограммы, характеризующие закономерности реализации случайной величины.

Для исследования полученные в эксперименте распределения заменяются теоретическими (аналитическими), удобными для математических исследований изучаемых величин или явлений.

Выбор теоретических законов определяется двумя условиями:

1 – хорошая аппроксимация результатов натурных наблюдений или экспери-ментов;

2 – удобство математических операций.

Видов теоретических законов распределения известно много.

Среди теоретических законов во многих отраслях науки наибольшее значение имеет закон нормального распределения. Важность закона нормального распределения подтверждается одной из главных теорем теории вероятностей – центральной предельной теоремы А.М. Ляпунова, следствие из которой может быть сформулировано следующим образом:

если случайная величина х представляет собой сумму большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму (т. е. на случайную величину х) мало, то случайная величина х имеет распределение, близкое к нормальному.

Закон нормального распределения и его свойства

Закон нормального распределения описывается функцией плотности вероятности

f(x) =	1	еxp [	- (x – x )2	],
	2		22

где  – среднеквадратичное отклонение случайной величины х, имеющей математическое ожидание х.

Некоторые свойства нормального распределения

Функция вероятности нормального распределения имеет вид

Среднеквадратическое отклонение (стандартное отклонение, стандарт)  - в теории вероятностей и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно её математического ожидания.

Измеряется в единицах измерения самой случайной величины. Равно корню квадратному из дисперсии случайной величины. Стандартное отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

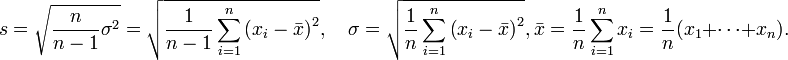
где   — стандарт, стандартное отклонение, несмещенная оценка среднеквадра-тического отклонения случайной величины X относительно её математического ожидания;  — дисперсия;  — i-й элемент выборки;  — среднее арифметическое выборки;  — объём выборки.

Следует отметить отличие стандарта (в знаменателе n − 1) от корня из дисперсии (среднеквадратического отклонения) (в знаменателе n), при малом объёме выборки оценка дисперсии через последнюю величину является несколько смещенной, при бесконечно большом объёме выборки разница между указанными величинами исчезает.