5. Предельный признак сравнения (теорему док.)

Пусть имеется два знакоположительных ряда 1)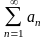 2) .

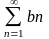Если существует конечный предел , то

1. если ряд (1) сходится, 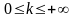,то ряд (2) сходится

2. если ряд (1) расходится, ,то (2) расходится.

В частности получаем, если 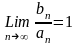, то (1) и (2) либо вместе сходятся, либо расходятся.

Доказательство:

1) По условию теоремы

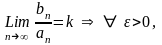
Рассматривая модуль, получим ;

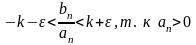
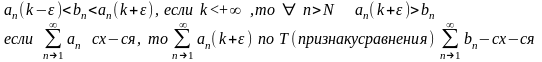
2) k>0 , выбираем значения 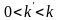,если (1) расходится, то , где , -расходится (по признаку сравнения).

6. Признак Даламбера, радикальный и интегральный Коши(3 теоремы док.).

Признак Даламбера.

Пусть 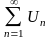- ряд с неотрицательными членами.

Если , то

а) - ряд -сходится;

б) 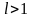- ряд - расходится;

в) - о сходимости ничего нельзя сказать.

3 Эталон: обобщенный гармонический ;

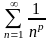Доказательство:

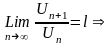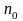По условию теоремы, , начиная с будет выполняться условие ;

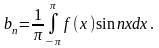
а) Пусть 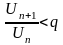начиная с :

;

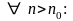
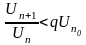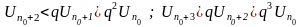
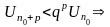члены исследуемого ряда меньше членов геометрической прогрессии 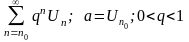; Геометрическая прогрессия сходится.

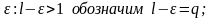
б) ; пусть для

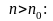
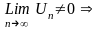ряд сходится.

Радикальный признак Коши.

Дан ряд ,есл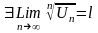и , то при

а) - ряд -сходится;

б) - ряд - расходится;

в) - о сходимости ничего нельзя сказать, предполагается что предел

Доказательство:

По условию теоремы, 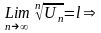, начиная с будет выполняться условие ;

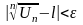а) 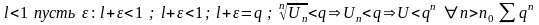- убывающая геометрическая прогрессия  по признаку сравнения 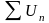- сходится, начиная с .

б) аналогично предыдущему.

Интегральный признак Коши.

Пусть дан ряд , члены этого ряда являются непрерывной функцией

g(x) при целых х и пусть функция g(x) является убывающей на промежутке ,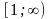

тогда ряд сходится, если сходится несобственный интеграл ,

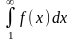и расходится, если расходится ;

Доказательство:

Рассмотрим площадь криволинейной трапеции

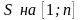
y(x)

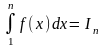
с другой стороны

1234……n-1 n

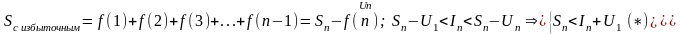
Пусть 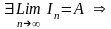из (*) следует - ограничена

по критерию ряд сходится.

Пусть не существует 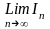или = следовательно из (**)следует - неограниченна, следовательно по критерию ряд сходится.

7. Знакопеременные ряды. Абсолютная и условная сходимость. Теорема об абсолютно сходящемся ряде(док).

Знакопеременные ряды - это ряды, которые содержат бесконечно много положительных и бесконечно много отрицательных членов. На ряду со знакопеременным рядом рассматривается ряд из абсолютных значений членов знакопеременного ряда.

-знакопеременный ряд.(1)

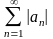-знакоположительный ряд.(2)

Теорема (критерий сходимости знакопеременного ряда).

Если ряд (2) сходится, то и ряд (1)- сходится.

Доказательство:

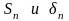частичные суммы рядов (1) (2) соответственно.

Обозначив через - сумму положительных членов ряда (1), - сумму отрицательных членов ряда(1).Тогда = - ; = -

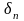Так как ряд (2) сходится, то существует конечный предел его частичных сумм =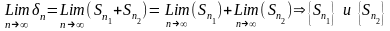 -ограничены.

Так как ряд (2) знакоположительный, то 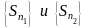- будут возрастающие, следовательно по теореме Вейерштрасса существует конечный предел этих последовательностей ( )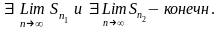

Рассмотрим - число конечное, следовательно (1)- сходится. Ч.Т.Д.

При исследовании знакопеременного ряда на сходимость нужно всегда рассматривать ряд из абсолютных величин членов этого ряда.

Определение:

Знакопеременный ряд называется абсолютно сходящимся, если сходится знакоположительный ряд ,составленный из абсолютных значений его членов.

Теорема (об абсолютно сходящемся ряде).

Если ряд сходится, то знакопеременный ряд тоже сходится.

Доказательство:

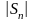для ряда ; для ряда состав. из модулей.

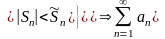сходится по признаку сравнения.

Признак этой теоремы является достаточным, но не является необходимым.

Ряд -сходится; ряд - расходится.

Определение:

Знакопеременный ряд называется условно сходящимся, если он сходится по признаку Лейбница, но ряд из абсолютных величин его членов расходится.