Вопрос 7

7. Осколочное действие авиационных средств поражения

Эффективность действия осколочных боеприпасов зависит от характеристик дробления оболочки заряда на осколки, т.е. от общего числа осколков, образующихся при взрыве, и от характера распространения осколков.

Характеристики дробления корпусов осколочных боеприпасов определяются опытным путем - подрывом в бронекамере, заполненной песком, водой или опилками.

После подрыва все собранные осколки сортируются по группам различной массы, подсчитывается число осколков в каждой группе и определяются геометрические размеры (длина, ширина, толщина) типичного осколка.

Полученные опытные данные являются основой для построения закона распределения осколков по их массам. Собираются осколки, масса которых превосходит некоторую минимальную массу q₀ , при этом масса максимального осколка, образовавшегося при взрыве, равна q_m. Диапазон возможных масс собранных осколков q₀q_m делят на отдельные интервалы:

q₀q₁;q₁q₂; ... ... ... ;q_{i -1}q_i; ... ... ... ; q_{m -1}q_m.

Обозначим величину интервала через q_i:q_i=q_i- q_{i -1}.

Обозначим общее число собранных осколков, масса которых больше, чем q₀, через N, а число осколков, принадлежащих группе q_{i -1}q_i, через N_i.

Тогда отношение 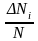представляет собой статистическую вероятность того, что взятый наугад осколок принадлежит данной группе, и равно относительному количеству осколков, масса которых заключена в интервале q_{i -1}q_i.

Закон распределения осколков по массам принято представлять в виде гистограммы распределения t^*(q) (рис.2.1).

Д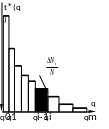 ля построения гистограммы t^*(q)

необходимо статическую вероятность

разделить не величину интервала

масс q_i:

Площадь каждого прямоугольника гистограммы равна относительному количеству осколков данной группы, ибо

Суммарная площадь всех прямоугольников гистограммы равна единице:

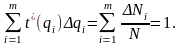
Гистограмма распределения t^*(q) полностью характеризует закон распределения осколков по их массам.Видно, что количество осколков малой массы больше количества осколков средней и большой массы.

Из-за наличия в металле оболочки различного рода структурных дефектов и неоднородностей (микротрещины, раковины), случайным образом распределенных по всему объему металла, процесс формирования осколков может существенно отличаться от рассмотренной схемы. Это придает процессу дробления оболочки случайный характер.

Управление процессом дробления оболочки с целью получения осколков заданной массы можно различными конструктивными методами:

• путем придания специальной формы;

• путем преднамеренного ослабления прочности стенок корпуса в соответствующих сечениях.

При расчетах эффективности осколочного действия необходимо знать число осколков, попавших в цель при данном взаиморасположении боевой части и цели.

В системе координат, связанной с боевой частью, направление дальнейшего полета осколка определяется двумя углами:

- углом  в меридиональной плоскости;

- углом  в экваториальной плоскости (рис.2.2).

При этом считают, что все осколки вылетающими из одной точкиО - центра массы боевой части. Так как все боеприпасы обладают осевой симметрией, то можно полагать, что в экваториальной плоскости все осколки распределяются равномерно.

Боевую часть подрывают в специальной мишенной обстановке, представляющую собой вертикальную стенку, выполненную в форме полуцилиндра: в центре полуцилиндра в горизонтальном положении устанавливается испытуемый образец (рис.2.3).

С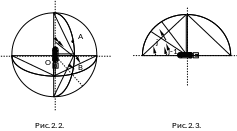 тенка обшивается материалом, при пробивании которого осколком образуется четкая пробоина (фанера, рубероид и т.д.). На стенке наносятся контуры проекции части сферы, заключенной между двумя меридиональными сечениями, угловое расстояние между которыми  определяет долю осколков, перехватываемых мишенной обстановкой и фиксируемых в опыте (действительное число осколков в 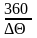раз

п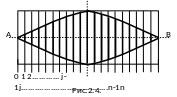 ревосходит число осколков, зафиксированных в данном опыте). На стенку наносятся вертикальные линии, соответствующие границам угловых секторов с некоторым шагом  (рис.2.4). Боевая часть при подрыве устанавливается на высоте средней линии АВ.

Мишенная обстановка позволяет зафиксировать пробоины от осколков, летящих в каждом из угловых интервалов . После проведения подрыва определяется число осколков Nj, попавших в каждый угловой сектор, и общее число осколков, перехваченных мишенной обстановкой N.

Отношение представляет собой статическую вероятность того, что осколок полетит в данном угловом секторе, и равно относительному числу осколков, летящих в угловом интервале _j-1_j.

Закон распределения осколков по направлениям разлета представляется в виде гистограммы (рис.2.5)

Площадь каждого прямоугольника гистограммы равна относительному количеству осколков . Суммарная площадь всех прямоугольников равна единице.

Вид закона распределения осколков по направлениям разлета определяется формой оболочки и заряда. У оболочек цилиндрической формы основное количество осколков разлетается в сравнительно узком угловом секторе, в направлении, совпадающим с нормалью к поверхности оболочки. Еще более узкий сектор разлета можно получить, придавая оболочке форму, изображенную на рис.2.6 (оболочки катушечной формы)

Рис.2.6

Рис.2.7

У оболочек, образующая которых имеет выпуклую форму (оболочки бочкообразной формы, рис.2.7), угловой сектор разлета осколков увеличивается тем в большей степени, чем больше кривизна образующей. На рис.2.8 изображены в качестве иллюстрации примерные виды законов распределения() для оболочек различной формы. У оболочек конической формы максимум закона распределения соответствует углам, примерно совпадающим с направлением перпендикуляра к поверхности оболочки.

()



90

180

Рис.2.8