10. Движение колесной пары с учетом деформации бандажа и рельса. Силы крипа

РЕКОМЕНДОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК

[1, гл. 5 § 5.2, § 5.3]

[2, гл. 3, п.п. 3.7]

[4, гл. 4]

Рассматриваемые вопросы:

1. Упругое проскальзывание (псевдоскольжение или крип);

2. Силы крипа;

3. Дифференциальные уравнения движения колесной пары;

10.1. Упругое проскальзывание (псевдоскольжение или крип)

Рис. 10.1. Деформация колеса в зоне контакта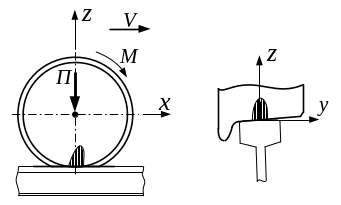

При передаче вертикальной силы от колеса на рельс возникает малая зона контакта с большими удельными давлениями – контактное пятно. В этом контактном пятне происходят упругие деформации. Если к колесу не приложены вращающий момент или горизонтальная сила, то пятно (зона контакта) симметрично относительно вертикальной оси. Зону контакта определяют на основе теории упругости. Площадь контакта представляет собой эллипс. Полуоси эллипса (размер эллипса) зависят от: радиусов кривизны контактирующих тел; нормального давления в зоне контакта; упругих постоянных этих тел.

Рис. 10.2. Зона контакта колеса и рельса

При движении колеса под действием вращающего момента симметрия распределения деформаций нарушается (рис.10.1). Зона контакта разделяется на две области (рис. 10.2). В области А сохраняется сцепление и происходят упругие деформации (в режиме тяги материал бандажа сжимается, а рельса растягивается), в области В происходят явления аналогичные боксованию.

Вследствие различия деформаций колеса и рельса в зоне контакта путь, пройденный геометрическим центром колеса, меньше пути, подсчитанного по угловой скорости вращения колеса в предположении качения без скольжения. Это явление с кинематической точки зрения рассматривают как проскальзывание, но учитывая причину его возникновения, такое проскальзывание называют упругим, псевдоскольжением или крипом.

10.2. Силы крипа

Касательные силы по площадке контакта, действующие на колесо, имеют проекцию на горизонтальную ось пути, направленную в сторону движения. Равнодействующую этих внешних сил называют силой крипа (в теории тяги поездов – силой сцепления). Для точного анализа явлений, происходящих в пятне контакта при движении колеса, необходимо использовать специальные методы теории упругости, пластичности.

В 1926 г. Ф. Картером получено, что продольные и поперечные силы крипа пропорциональны относительным скоростям скольжения. Проекции касательных сил крипа определяются выражениями:

; (10.1)

; (10.2)

где , - относительные скорости скольжения в направлении оси X и Y, соответственно, которые для точек B и D (см. рис. 9.3) определяется следующими выражениями:

, (10.3)

, (10.4)

где , - проекции скоростей проскальзывания на оси X и Y для точки В, определяемые по формулам (9.18) и (9.19).

С учетом формул (10.3), (10.4), (9.18) и (9.19) выражения для касательных сил крипа примут следующий вид:

; (10.5)

; (10.6)

где , - коэффициенты крипа, которые зависят от вертикальной силы, передаваемой от колеса на рельс, диаметра колеса, радиуса головки рельса, упругих постоянных. Знак “-” означает, что силы крипа направлены против скоростей проскальзывания. В простейшем случае коэффициенты крипа определяются следующим выражением:

; (10.7)

где - коэффициент, учитывающий влияние случайных факторов.

Данные экспериментов показывают, что силы крипа имеют большой разброс. Причиной этого являются вибрации, загрязнения поверхностей катания, температура, влажность и т.д. Поэтому значения коэффициента крипа могут изменяться в широких пределах. На основе лабораторных опытов установлено, что для верхней оценки можно использовать следующую формулу:

. (10.8)

Например для электровозов ВЛ80 при кН и м - кН.

Нижний предел коэффициента крипа можно определять по формуле:

. (10.9)

Для того же электровоза кН.

В общем случае помимо сил , продольной и поперечной могут быть все шесть реакций (три силы и три момента). Считается, что моменты и малы и их обычно не учитывают. Наиболее законченная теория взаимодействия колеса и рельса разработана Калкером, в которой дополнительно учитывается упругий момент “верчения” колесной пары относительно вертикальной оси, который называется спин .

Согласно этой теории силы крипа и момент спина определяются как произведения крипов в точке контакта колеса и рельса на коэффициенты крипов:

; (10.10)

; (10.11)

, (10.12)

где - коэффициент спина; - коэффициент крипа, характеризующий взаимное влияние поперечного крипа и спина .

Коэффициенты , , и определяются в зависимости от упругих свойств материалов колеса и рельса, радиуса колеса и нагрузки от колеса на рельс.

Например, для электровозов ВЛ80 кН, кН, кН, . Как видно много меньше других коэффициентов. Однако его необходимо учитывать так как, слагаемое, входящее в - оказывает значительное влияние при больших скоростях на устойчивость движения колесной пары. Кроме того, много меньше и однако слагаемое соизмеримо с .

Рис. 10.3. Зависимость силы крипа от относительной скорости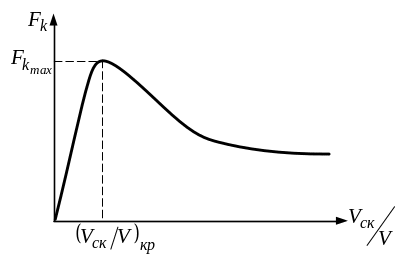

Силы крипа можно считать зависящим линейно от относительных скоростей проскальзывания лишь в ограниченном диапазоне последних. Начиная с некоторого предельного значения %, соответствующего максимальному значению силы трения, происходит срыв сцепления и возникает обычное, а не упругое скольжение, при котором сила трения убывает с ростом относительной скорости (рис. 10.3). Величина по результатам экспериментов определяется для разных состояний поверхностей рельсов (сухие, влажные, замасленные, с песком, вода с песком и т.д.).

Пример. Определим максимальную величину поперечного крипа при извилистом движении колесной пары. Величина поперечного крипа (относительная скорость скольжения) определяется выражением (см. формулу 8.21):

. (10.13)

Допустим, что максимальная величина возникает при выборе зазора в рельсовой колее ( м) и . Как и при кинематическом описании процесса извилистого движения колесной пары закон изменения колебания относа можно записать в следующем виде (см. формулу 8.15):

. (10.14)

Первая производная этого выражения имеет вид:

. (10.15)

При исследовании на экстремум, будем иметь:

. (10.16)

Тогда величина максимального поперечного крипа при будет определяться выражением:

. (10.17)

где - скорость скольжения точки контакта колеса и рельса поперек пути (вдоль оси y).

Для параметров электровоза ВЛ80 будем иметь:

. (10.18)

Эта величина меньше значения относительной скорости, соответствующей срыву сцепления (0,25 - 5%). Следовательно, только извилистое движение колесной пары не может быть причиной срыва сцепления.