
- •Основные задачи динамики локомотивов
- •Виды колебаний локомотивов
- •Возмущения, вызывающие колебания
- •Характеристики элементов соединений
- •Контрольные вопросы
- •Методика составления уравнений колебаний динамической модели экипажа
- •2.1. Принцип Даламбера
- •Динамическая модель экипажа
- •Составление уравнений вертикальных колебаний модели с одной степенью свободы при кинематическом возмущении
- •Контрольные вопросы
- •Составление уравнений вертикальных колебаний упрощенных динамических моделей
- •Уравнение колебаний модели с одной степенью свободы при силовом возмущении
- •Уравнения колебаний модели плоского двухосного экипажа
- •Контрольные вопросы
- •Свободные колебания динамических систем
- •4.1. Общие положения
- •4.2. Свободные колебания в недемпфированной системе
- •4.3. Свободные колебания в системе с гидравлическим гасителем
- •Контрольные вопросы
- •Матричная форма записи уравнений колебаний
- •5.1. Матричная форма записи уравнений колебаний в общем виде
- •5.2. Принцип составления уравнений колебаний в матричной форме на примере одноосной модели с двумя степенями свободы
- •Контрольные вопросы
- •Вынужденные колебания динамических систем
- •6.1. Понятие о возмущенном движении и методах исследования вынужденных колебаний
- •6.2. Частотный метод исследования вынужденных колебаний
- •6.3. Частотные характеристики модели с одной степенью свободы при кинематическом возмущении
- •Контрольные вопросы
- •Методика получения выражений амплитудных частотных (ачх) и фазовых частотных характеристик (фчх)
- •7.1. Преобразование чх системы с одной степенью свободы при кинематическом возмущении
- •7.2. Ачх и фчх системы с одной степенью свободы
- •7.3. Анализ ачх и фчх обобщенных координат
- •7.4. Чх динамической системы при силовом возмущении
- •Контрольные вопросы
- •Колебания при случайных возмущениях
- •8.1. Характеристики стационарных случайных процессов
- •8.2. Статистические характеристики случайного возмущения
- •8.3. Расчет показателей динамических качеств экипажной части
- •Контрольные вопросы
- •Боковые колебания локомотивов
- •9.1. Кинематическое описание процесса качения колесной пары по рельсам
- •Контрольные вопросы
Контрольные вопросы
В результате чего могут появляться свободные колебания?
Как определяется собственная частота недемпфированной системы?
Что называют периодом колебаний?
Что такое амплитуда колебаний?
Что такое коэффициент относительного затухания и как он определяется?
Что такое коэффициент критического затухания и как он определяется?
Какие процессы будут наблюдаться в системе при условии 1?
Какие процессы будут наблюдаться в системе при условии >1?
Какими параметрами характеризуется система, имеющая гаситель колебаний?
Матричная форма записи уравнений колебаний
РЕКОМЕНДОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК
[1, гл. 2 § 2.4, гл.4 § 4.1]
[4, гл. 1, п.п. 1.6]
[7, гл. 2, п.п. 2.2]
Рассматриваемые вопросы:
Матричная форма записи уравнений колебаний в общем виде (для системы с конечным числом степеней свободы);
Принцип составления уравнений колебаний в матричной форме на примере одноосной модели с двумя степенями свободы.
5.1. Матричная форма записи уравнений колебаний в общем виде
Динамические модели реальных локомотивов с точки зрения механики представляют собой системы с большим числом степеней свободы. Рассмотрим систему с k степенями свободы (с конечным числом степеней свободы). Колебания такой системы описываются системой дифференциальных уравнений общим числом k.
Такую систему удобно записывать в матричной форме. В общем виде система дифференциальных уравнений может быть записана в так называемой прямой форме
![]() ,
(5.1)
,
(5.1)
где
![]() - инерционная матрица;
- инерционная матрица;
![]() - диссипативная матрица;
- диссипативная матрица;
![]() -
матрица жесткостей;
-
матрица жесткостей;
![]() - вектор обобщенных сил, зависящих от
скорости движения и эквивалентной
геометрической неровности (матрица
неровностей);
- вектор обобщенных сил, зависящих от
скорости движения и эквивалентной
геометрической неровности (матрица
неровностей);
![]() - матрица столбец (вектор) ускорений
обобщенных координат;
- матрица столбец (вектор) ускорений
обобщенных координат;
![]() - матрица столбец
(вектор) скоростей обобщенных координат;
- матрица столбец
(вектор) скоростей обобщенных координат;
![]() - матрица столбец (вектор) обобщенных
координат.
- матрица столбец (вектор) обобщенных
координат.
, и - квадратные матрицы размером kk.
Правую часть можно рассматривать и как прямоугольную матрицу с числом столбцов, равных числу независимых комбинаций возмущения. Если считать кинематические возмущения по левой и правой рельсовым нитям независимыми, то таких столбцов будет два. В этом случае в левой части уравнения (5.1) вместо столбцов обобщенных координат, скоростей и ускорений также будут матрицы размером k2.
Если возмущения по обеим рельсовым нитям одинаковы, то вектор обобщенных сил находят путем линейного преобразования эквивалентной геометрической неровности, т.е.
![]() ,
(5.2)
,
(5.2)
где
![]() и
и
![]() - векторы размером k1,
элементы которых состоят из ординат
неровности и ее производной соответственно;
- векторы размером k1,
элементы которых состоят из ординат
неровности и ее производной соответственно;
![]() и
и
![]() - матрицы размером kk
преобразований кинематического
возмущения в обобщенные силы, элементы
которых зависят от параметров экипажа.
- матрицы размером kk
преобразований кинематического
возмущения в обобщенные силы, элементы
которых зависят от параметров экипажа.
В этом случае модель экипажа можно свести к плоской. Матричную форму записи уравнений удобно использовать в динамических моделях с количеством степеней свободы k>1.
5.2. Принцип составления уравнений колебаний в матричной форме на примере одноосной модели с двумя степенями свободы
Рисунок
5.1. Линейная одноосная модель как система
с двумя степенями свободы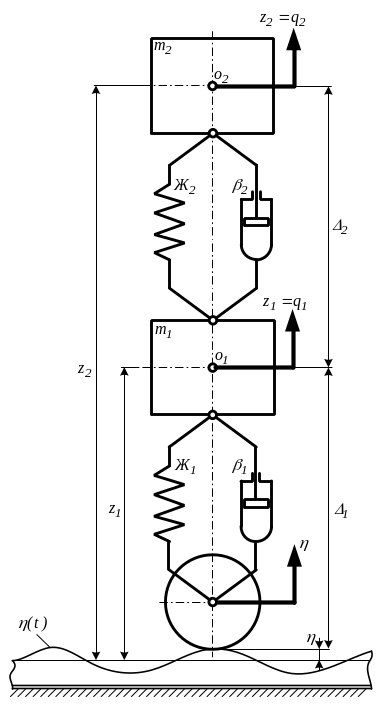
![]() - суммарная масса всех тележек локомотива,
масса
- суммарная масса всех тележек локомотива,
масса
![]() - масса кузова. Каждая из масс может
совершать вертикальные колебания,
поэтому система имеет две степени
свободы. Пружина с жесткостью
- масса кузова. Каждая из масс может
совершать вертикальные колебания,
поэтому система имеет две степени
свободы. Пружина с жесткостью
![]() и гаситель с коэффициентом затухания
и гаситель с коэффициентом затухания
![]() эквивалентны буксовому подвешиванию,
а пружина и гаситель с характеристиками
эквивалентны буксовому подвешиванию,
а пружина и гаситель с характеристиками
![]() и
и
![]() эквивалентны центральному подвешиванию.
Рассмотрим колебания динамической
системы при кинематическом возмущении.
Составим уравнения сил, действующих на
каждую массу, в соответствии с принципом
Даламбера. Для этого необходимо поочередно
зафиксировать (“мысленно закрепить”)
каждую массу.
эквивалентны центральному подвешиванию.
Рассмотрим колебания динамической
системы при кинематическом возмущении.
Составим уравнения сил, действующих на
каждую массу, в соответствии с принципом
Даламбера. Для этого необходимо поочередно
зафиксировать (“мысленно закрепить”)
каждую массу.
Для массы при фиксировании уравнение действующих сил будет иметь вид
![]() .
(5.3)
.
(5.3)
Аналогично фиксируя , получим уравнение для массы
![]() .
(5.4)
.
(5.4)
Выражения
для сил, входящих в уравнения (5.3) и (5.4),
с учетом того, что
![]() и
и
![]() имеют вид
имеют вид
![]() ,
(5.5)
,
(5.5)
![]() ,
(5.6)
,
(5.6)
![]() ,
(5.7)
,
(5.7)
![]() ,
(5.8)
,
(5.8)
![]() ,
(5.9)
,
(5.9)
![]() .
(5.10)
.
(5.10)
Подставляя выражения (5.5)…(5.10) в уравнения (5.3) и (5.4), получим уравнения колебаний динамической модели.
Для массы имеем
![]() .
(5.11)
.
(5.11)
Для массы имеем
![]() .
(5.12)
.
(5.12)
Полученные уравнения колебаний в совокупности представляют собой систему дифференциальных уравнений (в данном случае их два, так как k=2).
Как видно из этой системы уравнений, колебания обоих масс связаны, так как в оба уравнения входят обобщенные координаты перемещений , скоростей и ускорений . Между координатами этой системы имеется упруго-диссипативная связь. Запишем систему в матричной форме.
Правило записи в матричную форму:
Записываются полученные уравнения в систему, при этом в каждом уравнении на первом месте стоят члены, относящиеся к координате
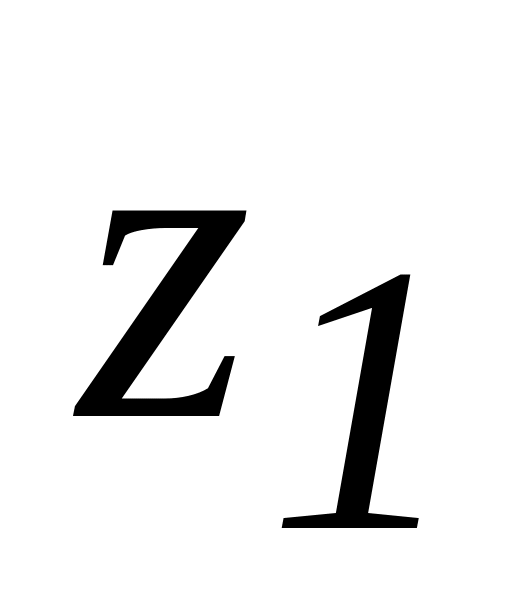 начиная с производной наибольшего
порядка.
начиная с производной наибольшего
порядка.Заготавливаются формы матриц , и размером kk (в рассматриваемом примере - 22), а матриц
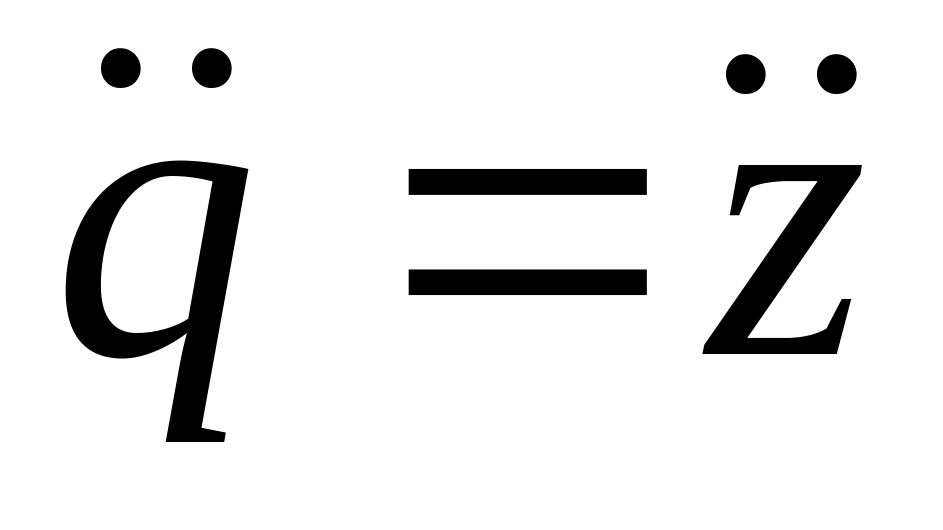 ,
,
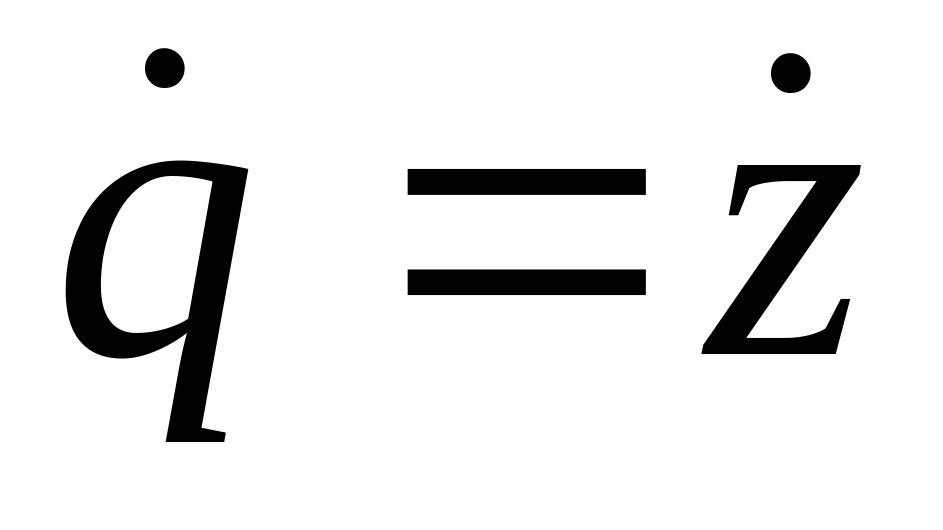 ,
,
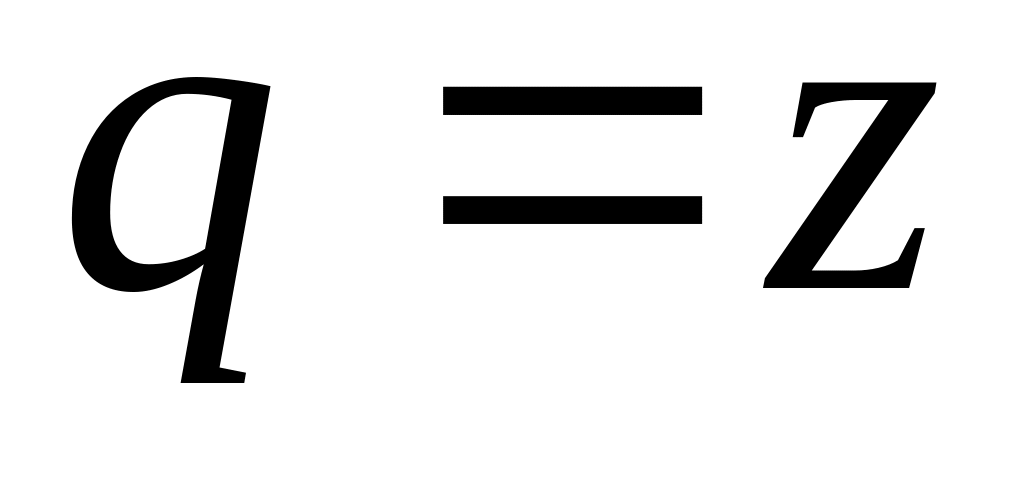 размером k1
(в рассматриваемом примере - 21).
размером k1
(в рассматриваемом примере - 21).Заполняются матрицы, начиная с координаты
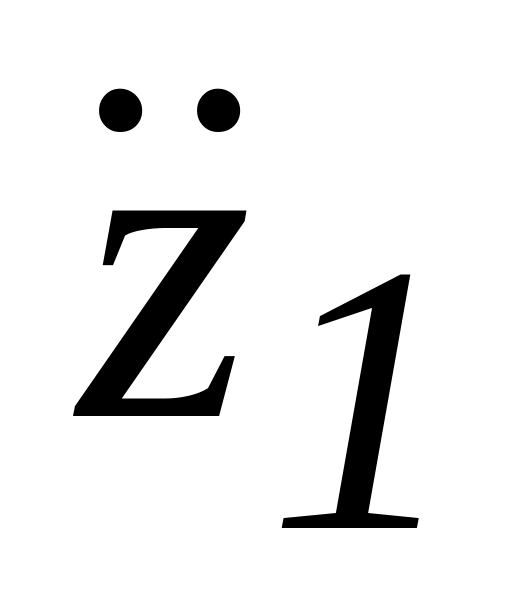 далее
далее
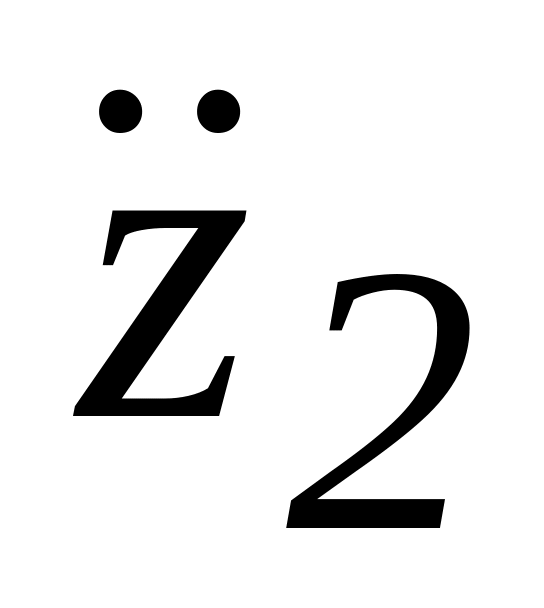 и т.д.
и т.д.
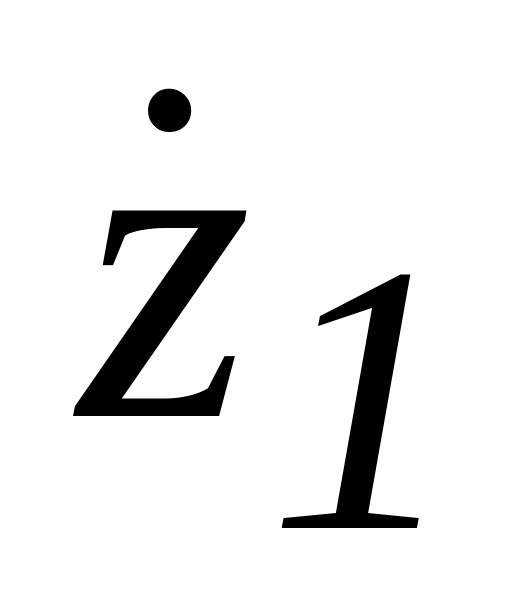 -
-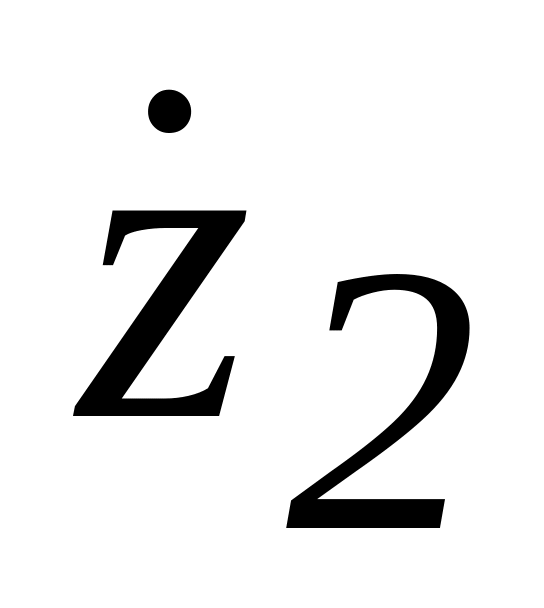 ,
-
,
-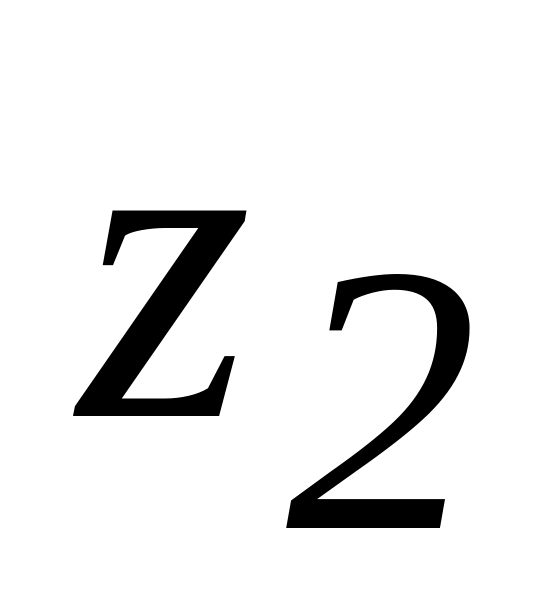 .
.
Для рассматриваемого примера уравнения колебаний (5.11) и (5.12) в матричной форме будут иметь следующий вид
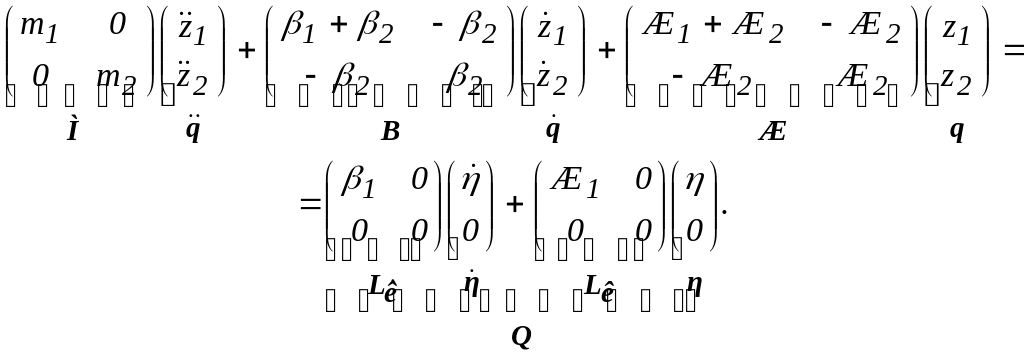 (5.13)
(5.13)
Матрица является диагональной, если отсутствуют инерционные связи между координатами. При наличии этих связей в матрице появятся элементы не стоящие на диагонали.
Матрица и являются пропорциональными если гидравлические гасители стоят параллельно каждому упругому элементу (пружине).
Отклонение любой из масс по своей координате вызывает появление упругих и диссипативных сил, препятствующих этому отклонению. Поэтому такая система является устойчивой. Кроме того, если задать начальной отклонение любой из масс, то колебательное движение будет затухающим из-за наличия гасителей. Поэтому в вертикальной плоскости колебания любого экипажа являются устойчивыми.
