
- •Основные задачи динамики локомотивов
- •Виды колебаний локомотивов
- •Возмущения, вызывающие колебания
- •Характеристики элементов соединений
- •Контрольные вопросы
- •Методика составления уравнений колебаний динамической модели экипажа
- •2.1. Принцип Даламбера
- •Динамическая модель экипажа
- •Составление уравнений вертикальных колебаний модели с одной степенью свободы при кинематическом возмущении
- •Контрольные вопросы
- •Составление уравнений вертикальных колебаний упрощенных динамических моделей
- •Уравнение колебаний модели с одной степенью свободы при силовом возмущении
- •Уравнения колебаний модели плоского двухосного экипажа
- •Контрольные вопросы
- •Свободные колебания динамических систем
- •4.1. Общие положения
- •4.2. Свободные колебания в недемпфированной системе
- •4.3. Свободные колебания в системе с гидравлическим гасителем
- •Контрольные вопросы
- •Матричная форма записи уравнений колебаний
- •5.1. Матричная форма записи уравнений колебаний в общем виде
- •5.2. Принцип составления уравнений колебаний в матричной форме на примере одноосной модели с двумя степенями свободы
- •Контрольные вопросы
- •Вынужденные колебания динамических систем
- •6.1. Понятие о возмущенном движении и методах исследования вынужденных колебаний
- •6.2. Частотный метод исследования вынужденных колебаний
- •6.3. Частотные характеристики модели с одной степенью свободы при кинематическом возмущении
- •Контрольные вопросы
- •Методика получения выражений амплитудных частотных (ачх) и фазовых частотных характеристик (фчх)
- •7.1. Преобразование чх системы с одной степенью свободы при кинематическом возмущении
- •7.2. Ачх и фчх системы с одной степенью свободы
- •7.3. Анализ ачх и фчх обобщенных координат
- •7.4. Чх динамической системы при силовом возмущении
- •Контрольные вопросы
- •Колебания при случайных возмущениях
- •8.1. Характеристики стационарных случайных процессов
- •8.2. Статистические характеристики случайного возмущения
- •8.3. Расчет показателей динамических качеств экипажной части
- •Контрольные вопросы
- •Боковые колебания локомотивов
- •9.1. Кинематическое описание процесса качения колесной пары по рельсам
- •Контрольные вопросы
Контрольные вопросы
Что является причиной силового возмущения?
Какие задачи решаются при силовом способе задания возмущения?
Какие особенности позволяет учитывать плоская модель двухосного экипажа?
Какие виды колебаний позволяет исследовать плоская модель?
Что называют транспортным запаздыванием, и от каких параметров оно зависит?
Как определяются прогибы рессорных комплектов при наличии двух видов колебаний?
Свободные колебания динамических систем
РЕКОМЕНДОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК
[1, гл. 2 § 2.4, гл.4 § 4.1]
[4, гл. 1, п.п. 1.5]
Рассматриваемые вопросы:
Общие положения;
Свободные колебания в недемпфированной системе;
Свободные колебания в системе с гидравлическим гасителем.
4.1. Общие положения
Свободные колебания динамических систем возникают при отсутствии переменного внешнего воздействия вследствие действия однократно приложенного и больше не повторяющегося воздействия. Свободные колебания рельсовых экипажей появляются при проведении опыта по сбрасыванию экипажа с клиньев, при ударе колеса с “ползуном” о рельс и т.п. Сбрасывание с клиньев выполняют для получения информации об упругих и диссипативных свойствах рессорного подвешивания экипажа. При проходе изолированной неровности одновременно происходят как свободные, так и вынужденные колебания.
После действия однократного воздействия предполагается, что система начинает двигаться по отношению к положению равновесия. Исследовать свободные колебания будем на примере линейной модели с одной степенью свободы.
4.2. Свободные колебания в недемпфированной системе
Напомним основные результаты, полученные при составлении уравнений колебаний для линейной системы с одной степенью свободы (см. гл.2, п.п. 2.3). Колебание подпрыгивания описываются уравнением (см. формулу 2.19), которое имеет вид
![]() .
(4.1)
.
(4.1)
Условием свободных
колебаний является равенство нулю
правой части данного уравнения, т.е.
![]() (внешнее возмущение отсутствует), и
принимая =0,
получим следующее уравнение
(внешнее возмущение отсутствует), и
принимая =0,
получим следующее уравнение
![]() .
(4.2)
.
(4.2)
Разделив оба члена на
массу m и приняв
![]() ,
получим
,
получим
![]() .
(4.3)
.
(4.3)
где
![]() - собственная (круговая) частота
недемпфированной системы, являющаяся
внутренним параметром системы.
- собственная (круговая) частота
недемпфированной системы, являющаяся
внутренним параметром системы.
Это
уравнение описывает колебательный
процесс с частотой
.
Решение данного уравнения при начальных
условиях
![]() и
и
![]() будет иметь вид
будет иметь вид
![]() .
(4.4)
.
(4.4)
где
![]() - амплитуда начального воздействия.
- амплитуда начального воздействия.
График
функции
![]() для исходных данных m=5
т, Ж=1500 кН/м и начальным воздействием
для исходных данных m=5
т, Ж=1500 кН/м и начальным воздействием
![]() ,
будет иметь вид, показанный на рисунке
4.1.
,
будет иметь вид, показанный на рисунке
4.1.
Рисунок
4.1. Свободные колебания в системе без
гасителя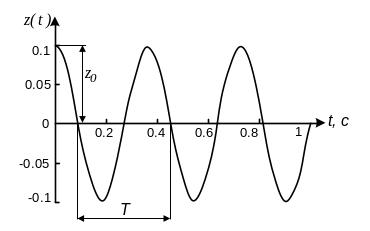
Под амплитудой колебаний понимается наибольшее за полупериод отклонение системы от положения равновесия.
Вывод: Система с одной степенью свободы, будучи выведена из положения равновесия малым возмущением, неограниченно долго будет совершать гармонические колебания.
4.3. Свободные колебания в системе с гидравлическим гасителем
Рассмотрим теоретические основы демпфирования применительно к модели с одной степенью свободы (см. гл.2, п.п. 2.3).
Дифференциальное уравнение свободных колебаний данной модели ( ), с учетом демпфирования имеет вид
![]() .
(4.5)
.
(4.5)
Разделив все члены уравнения на массу m, получим
![]() ,
(4.6)
,
(4.6)
где n – коэффициент относительного затухания, который определяется
![]() .
(4.7)
.
(4.7)
где
![]() - коэффициент критического
затухания, т.е. наименьшее значение
коэффициента затухания, при котором
движение системы перестает быть
колебательным.
- коэффициент критического
затухания, т.е. наименьшее значение
коэффициента затухания, при котором
движение системы перестает быть
колебательным.
При
![]()
![]() или n1
свободное движение системы носит
колебательный характер, при
или n1
движение перестает быть колебательным
и становится апериодическим.
или n1
свободное движение системы носит
колебательный характер, при
или n1
движение перестает быть колебательным
и становится апериодическим.
Коэффициент критического затухания определяется
![]() .
(4.8)
.
(4.8)
Записав частное решение уравнения (4.6) в виде
![]() ,
(4.9)
,
(4.9)
получим характеристическое уравнение
![]() .
(4.10)
.
(4.10)
Корни данного характеристического уравнения определяются
![]() . (4.11)
. (4.11)
В зависимости от
соотношения
![]() и
и
![]() возможны три случая:
возможны три случая:
а)
или
1
- случай малого сопротивления в
системе. Под корнем получится
отрицательное число. Вынесем из под
корня -
,
и введем мнимую единицу
![]() ,
получим
,
получим
![]() ,
(4.12)
,
(4.12)
где
![]() - степень затухания;
- степень затухания;
![]() - частота свободных колебаний демпфированной
системы.
- частота свободных колебаний демпфированной
системы.
С учетом введенных обозначений и наличием двух корней, общее решение уравнения 4.6 запишем в следующем виде
![]() .
(4.13)
.
(4.13)
Подставим в данное уравнение значения корней, получим
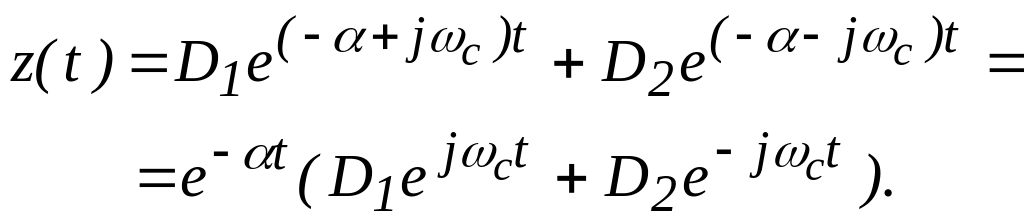 (4.14)
(4.14)
Считая,
что
![]() и
и
![]() в общем случае являются комплексными
числами, и используя формулу Эйлера для
перехода от показательной к алгебраической
форме, получим
в общем случае являются комплексными
числами, и используя формулу Эйлера для
перехода от показательной к алгебраической
форме, получим
![]() .
(4.15)
.
(4.15)
где
![]() и
и
![]() - постоянные, определяемые из начальных
условий.
- постоянные, определяемые из начальных
условий.
Для
исходных данных m=5
т, Ж=1500 кН/м и начальным воздействием
,
-
![]() кНс/м. Примем коэффициент диссипации
гасителя меньше, чем
,
а именно
кНс/м. Примем коэффициент диссипации
гасителя меньше, чем
,
а именно
![]() кНс/м.
кНс/м.
График колебательного процесса будет иметь вид, показанный на рисунке 4.2.
Рисунок
4.2. Свободные колебания в системе с
гасителем при условии
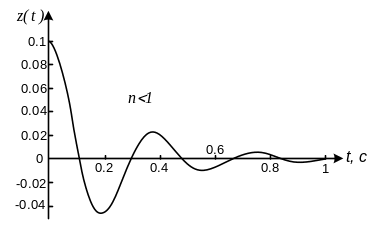
![]() меньшей, чем
,
т.е. силы сопротивления увеличивают
период колебаний.
меньшей, чем
,
т.е. силы сопротивления увеличивают
период колебаний.
б) > или >1 - случай большого сопротивления в системе.
В этом случае корни
![]() характеристического уравнения (4.11)
получаются действительными и
отрицательными. Так как корни отрицательные,
то с течением времени
будет убывать по апериодическому закону.
Для аналогичных исходных данных, но с
коэффициентом диссипации гасителя
характеристического уравнения (4.11)
получаются действительными и
отрицательными. Так как корни отрицательные,
то с течением времени
будет убывать по апериодическому закону.
Для аналогичных исходных данных, но с
коэффициентом диссипации гасителя
![]() кНс/м большим, чем
,
график функции
будет иметь вид, показанный на рисунке
4.3.
кНс/м большим, чем
,
график функции
будет иметь вид, показанный на рисунке
4.3.
Рисунок
4.3. Свободные колебания в системе с
гасителем при условии
>
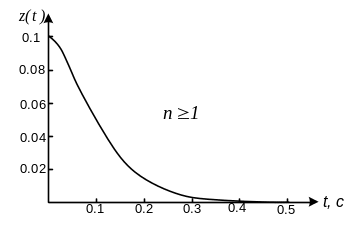
в) = или =1 - случай критического сопротивления в системе.
Данный случай можно рассматривать как разновидность случая с большим затуханием, при этом корни уравнения (4.11) получаются действительными, отрицательными и кратными. Характер изменения функции этого процесса будет аналогичен графику на рисунке 4.3.
На
реальном подвижном составе коэффициент
диссипации гасителя
делают меньшим, чем
,
так в буксовой ступени коэффициент
относительного затухания принимают
![]() =0,3…0,4,
в центральном подвешивании
=0,3…0,4,
в центральном подвешивании
![]() =0,2…0,3.
=0,2…0,3.
Если принять =0,3, проводя вычисления амплитуды можно показать, что за три периода происходит уменьшение амплитуды примерно в 310 раз, но период колебаний увеличится примерно на 5%.
Вывод:
При рассмотрении свободных колебаний
можно пренебрегать сопротивлением
гасителя, однако его необходимо учитывать
при определении амплитуды колебаний.
Система с демпфированием характеризуется
двумя параметрами
и
![]() ,
т.е. свойства колебаний зависят от
собственных свойств системы.
Кроме того, характеристики свободных
колебаний – численные значения амплитуд
и фаз собственных колебаний зависят от
величины начальных условий.
,
т.е. свойства колебаний зависят от
собственных свойств системы.
Кроме того, характеристики свободных
колебаний – численные значения амплитуд
и фаз собственных колебаний зависят от
величины начальных условий.
В зависимости от характера свободного движения, возникающего под действием начальных возмущений, динамическая система может быть устойчивой, если значения обобщенных координат остаются ограниченными или неустойчивой в противном случае. Вертикальные колебания экипажа всегда ограничены. Боковые колебания могут быть неустойчивыми, это происходит при превышении определенной скорости движения (критической). Особенности боковых колебаний будут рассмотрены в последующих главах.
