
- •Основные задачи динамики локомотивов
- •Виды колебаний локомотивов
- •Возмущения, вызывающие колебания
- •Характеристики элементов соединений
- •Контрольные вопросы
- •Методика составления уравнений колебаний динамической модели экипажа
- •2.1. Принцип Даламбера
- •Динамическая модель экипажа
- •Составление уравнений вертикальных колебаний модели с одной степенью свободы при кинематическом возмущении
- •Контрольные вопросы
- •Составление уравнений вертикальных колебаний упрощенных динамических моделей
- •Уравнение колебаний модели с одной степенью свободы при силовом возмущении
- •Уравнения колебаний модели плоского двухосного экипажа
- •Контрольные вопросы
- •Свободные колебания динамических систем
- •4.1. Общие положения
- •4.2. Свободные колебания в недемпфированной системе
- •4.3. Свободные колебания в системе с гидравлическим гасителем
- •Контрольные вопросы
- •Матричная форма записи уравнений колебаний
- •5.1. Матричная форма записи уравнений колебаний в общем виде
- •5.2. Принцип составления уравнений колебаний в матричной форме на примере одноосной модели с двумя степенями свободы
- •Контрольные вопросы
- •Вынужденные колебания динамических систем
- •6.1. Понятие о возмущенном движении и методах исследования вынужденных колебаний
- •6.2. Частотный метод исследования вынужденных колебаний
- •6.3. Частотные характеристики модели с одной степенью свободы при кинематическом возмущении
- •Контрольные вопросы
- •Методика получения выражений амплитудных частотных (ачх) и фазовых частотных характеристик (фчх)
- •7.1. Преобразование чх системы с одной степенью свободы при кинематическом возмущении
- •7.2. Ачх и фчх системы с одной степенью свободы
- •7.3. Анализ ачх и фчх обобщенных координат
- •7.4. Чх динамической системы при силовом возмущении
- •Контрольные вопросы
- •Колебания при случайных возмущениях
- •8.1. Характеристики стационарных случайных процессов
- •8.2. Статистические характеристики случайного возмущения
- •8.3. Расчет показателей динамических качеств экипажной части
- •Контрольные вопросы
- •Боковые колебания локомотивов
- •9.1. Кинематическое описание процесса качения колесной пары по рельсам
- •Контрольные вопросы
Контрольные вопросы
В чем заключается сущность принципа Даламбера?
Что понимается под силой инерции?
От каких параметров зависит реакция на путь при движении одиночного колеса?
Что называют динамической моделью экипажной части?
Какими параметрами характеризуется динамическая модель?
Что такое число степеней свободы?
Что называют обобщенными координатами?
Как определяются упругие и диссипативные силы в модели с одной степенью свободы?
Какой обобщенной координатой характеризуются колебания модели с одной степенью свободы?
Почему используя модель с одной степенью свободы можно только приближенно оценить ее динамические свойства?
Составление уравнений вертикальных колебаний упрощенных динамических моделей
РЕКОМЕНДОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК
[1, гл. 4 § 4.1]
[7, гл. 2, п.п. 2.2]
Рассматриваемые вопросы:
Уравнение колебаний модели с одной степенью свободы при силовом возмущении;
Уравнения колебаний модели плоского двухосного экипажа.
Уравнение колебаний модели с одной степенью свободы при силовом возмущении
Рисунок
3.1. Плоская модель с одной степенью
свободы при силовом возмущении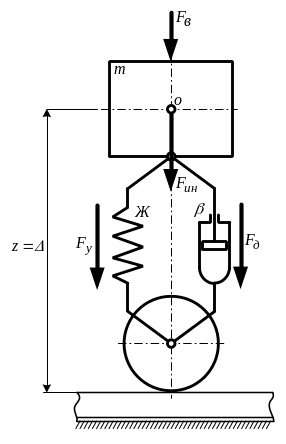
![]() ,
появляющаяся при работе мотор –
компрессоров, мотор – вентиляторов,
дизельной установки и других элементов
оборудования. В этом случае имеет место
силовой способ задания возмущения и
соответствующая расчетная схема,
представленная на рисунке 2.5. Обозначения,
принятые для этой схемы, аналогичны
обозначениям на рисунке 2.4. Принято, что
кинематическое возмущение отсутствует,
а закон изменения силового возмущения
во времени задан.
,
появляющаяся при работе мотор –
компрессоров, мотор – вентиляторов,
дизельной установки и других элементов
оборудования. В этом случае имеет место
силовой способ задания возмущения и
соответствующая расчетная схема,
представленная на рисунке 2.5. Обозначения,
принятые для этой схемы, аналогичны
обозначениям на рисунке 2.4. Принято, что
кинематическое возмущение отсутствует,
а закон изменения силового возмущения
во времени задан.
Согласно принципа Даламбера, уравнение вертикальных колебаний динамической модели имеет вид
![]() .
(3.1)
.
(3.1)
Так как кинематическое
возмущение отсутствует (![]() ),
то упругая и диссипативная силы
определяются соответственно
),
то упругая и диссипативная силы
определяются соответственно
![]() ,
(3.2)
,
(3.2)
![]() .
(3.3)
.
(3.3)
Сила инерции определяется по формуле 2.14. Подставим выражения 2.14, 3.2 и 3.3 в уравнение колебаний 3.1. Поучим следующее окончательное уравнение
![]() .
(3.4)
.
(3.4)
Решение данного уравнение позволяет решать задачи виброзащиты силового оборудования локомотивов от вращения несбалансированных частей.
Уравнения колебаний модели плоского двухосного экипажа
Пользуясь такой моделью, можно получить более подробную информацию о динамических свойствах локомотива. Появляется возможность учесть, кроме подпрыгивания, еще и колебания галопирования, а также неодновременность задания (запаздывания) возмущения под две колесные пары.
Рисунок
3.2. Плоская модель двухосного экипажа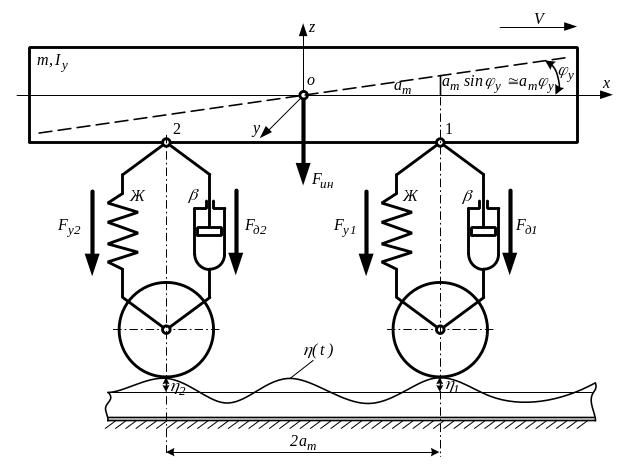
В модели масса m
(тележка) совершает колебания подпрыгивания
и галопирования
![]() .
Причиной колебаний являются возмущения
.
Причиной колебаний являются возмущения
![]() и
и
![]() передаваемые через первую и вторую
колесные пары. При движении экипажа с
поступательной скоростью V,
неровность
повторяет неровность
,
через некоторое время ,
называемым транспортным
запаздыванием.
Это время определяется скоростью
движения V
и расстоянием между осями колесных пар
передаваемые через первую и вторую
колесные пары. При движении экипажа с
поступательной скоростью V,
неровность
повторяет неровность
,
через некоторое время ,
называемым транспортным
запаздыванием.
Это время определяется скоростью
движения V
и расстоянием между осями колесных пар
![]() ,
то есть
,
то есть
![]() .
(3.5)
.
(3.5)
Поэтому выражения для неровностей под первой и второй колесными парами можно записать в следующем виде
![]() ,
(3.6)
,
(3.6)
![]() ,
(3.7)
,
(3.7)
где
![]() - единичное возмущающее входное
воздействие.
- единичное возмущающее входное
воздействие.
Уравнение колебания подпрыгивания с использованием принципа Даламбера имеет следующий вид
![]() .
(3.8)
.
(3.8)
Перемещения в точках 1 и 2 складываются из колебаний подпрыгивания и вертикальных составляющих угловых колебаний галопирования , (см. рисунок 3.2) то есть
![]() ,
(3.9)
,
(3.9)
![]() .
(3.10)
.
(3.10)
С учетом малости угла
,
то есть
![]() ,
выражения 3.9 и 3.10 примут следующий вид
,
выражения 3.9 и 3.10 примут следующий вид
![]() ,
(3.11)
,
(3.11)
![]() .
(3.12)
.
(3.12)
Силы, входящие в уравнение вертикальных колебаний (формула 3.8) с учетом формул 3.11 и 3.12 определяются
![]() ,
(3.13)
,
(3.13)
![]() ,
(3.14)
,
(3.14)
![]() ,
(3.15)
,
(3.15)
![]() ,
(3.16)
,
(3.16)
![]() .
(3.17)
.
(3.17)
Подставим выражения 3.13…3.17 в уравнение вертикальных колебаний (формула 3.8), получим
![]() (3.18)
(3.18)
Раскрывая скобки и выполняя преобразования с подобными слагаемыми, получим окончательное уравнение колебания подпрыгивания
![]() .
(3.19)
.
(3.19)
Для вывода уравнения колебания галопирования необходимо составить уравнение моментов относительно оси y, проходящей через центр тяжести экипажа О. Уравнение будет иметь следующий вид
![]() .
(3.20)
.
(3.20)
Моменты, входящие в уравнение (формула 3.20) определяются
![]() ,
(3.21)
,
(3.21)
где
![]() - момент инерции массы m
относительно оси y.
- момент инерции массы m
относительно оси y.
![]() ,
(3.22)
,
(3.22)
![]() ,
(3.23)
,
(3.23)
![]() ,
(3.24)
,
(3.24)
![]() .
(3.25)
.
(3.25)
Подставим выражения 3.21…3.25 в уравнение колебания галопирования (формула 3.20) и выполняя преобразования с подобными слагаемыми, как это сделано в уравнении подпрыгивания, получим окончательное уравнение колебания галопирования получим
![]() . (3.26)
. (3.26)
Таким образом, колебания рассматриваемой модели описываются двумя уравнениями (3.19) и (3.26). Как видно из этих уравнений, колебания галопирования и подпрыгивания тележки не связаны. Эта модель позволяет получить разные значения ускорений и перемещений по длине экипажа и различные показатели динамики в комплектах рессорного подвешивания, что в большей мере соответствует реальным схемам.
