2. Методика составления уравнений колебаний динамической модели экипажа

РЕКОМЕНДОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК

[1, гл. 2 § 2.1, 2.4, гл.4 § 4.1]

[2, гл. 2, п.п. 2.3]

[7, гл. 2, п.п. 2.2]

Рассматриваемые вопросы:

1. Принцип Даламбера;

2. Динамическая модель экипажа;

3. Составление уравнений вертикальных колебаний модели с одной степенью свободы при кинематическом возмущении.

2.1. Принцип Даламбера

Рис. 2.1. Схема сил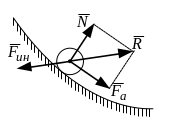

Аналитическая механика основывается на том или ином принципе – аксиоматическом утверждении. Для составления уравнений движения может использоваться принцип Даламбера, согласно которому уравнениям движения можно придать вид уравнений равновесия, если ко всем точкам системы приложить дополнительно силы инерции.

Рассмотрим принцип Даламбера. Допустим, что материальная точка под действием активной силы движется по связи (рис. 2.1). Ускорение будет направлено по равнодействующей силы R. Векторная сумма активной силы и силы реакции  будет определяться

. (2.1)

Тогда

, (2.2)

где - сила инерции (знак «-» означает, что сила инерции направлена против ускорения )

Принцип Даламбера (определение)

Если к действующей на тело активной силы и реакции связи приложить дополнительную силу инерции, то тело будет находиться в равновесии (сумма всех сил, действующих в системе, дополненная главным вектором инерции равна нулю).

Рис. 2.2. Поднятие груза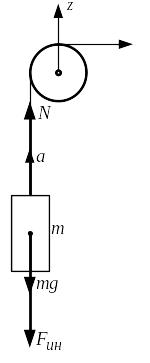

Под силой инерции понимается вектор, численно равный произведению массы на ускорение и направленный против ускорения. Этот принцип придает уравнениям движения формальный вид уравнений равновесия. С помощью принципа Даламбера удобно определять реакции связей. Рассмотрим на примерах.

Пример 1. Поднятие груза массой m (рис.2.2).

Согласно принципу Даламбера, после добавления силы инерции система находится в равновесии или сумма проекций всех сил на вертикальную ось z равна нулю, то есть

, (2.3)

или

. (2.4)

Реакция N определяется

. (2.5)

Вывод: Из полученного выражения видно, что чем больше ускорение , тем больше реакция N, поэтому поднимать груз большой массы необходимо с меньшим ускорением.

Пример 2. Движение колеса по неровности пути (рис.2.3).

Рис. 2.3. Движение колеса по неровности

2b– высота неровности;

x – текущая координата;

V – скорость движения;

m – масса колеса;

L – длина неровности.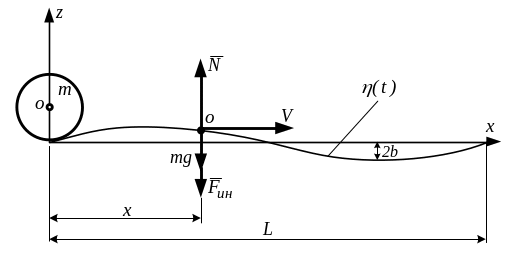

Рассмотрим движение одиночного колеса с массой m по абсолютно жесткому пути. Расчетная схема имеет вид, показанный на рис. 2.3.

Проведенными исследованиями доказано, что большинство неровностей имеют синусоидальный и косинусоидальный характер.

Допустим, что форма неровности приведенной на рис. 2.3. с достаточной точностью описывается уравнением

. (2.6)

Обозначая поступательную скорость колеса через V, пройденный путь колесом от начала неровности (текущая координата) определяется

. (2.7)

Подставив значение x в формулу 2.6, получим

. (2.8)

Так как путь абсолютно жесткий, то при прохождении колеса деформация пути отсутствует. В этом случае вертикальное перемещение колеса (траектория движения колеса) будет определяться формой неровности, то есть .

Вертикальная скорость колеса по оси z есть первая производная от его перемещения

. (2.9)

Вертикальное ускорение колеса по оси z есть вторая производная от его перемещения

. (2.10)

Сила инерции колеса определяется

. (2.11)

Используя принцип Даламбера, составим уравнение равновесия сил показанных на рис. 2.3

. (2.12)

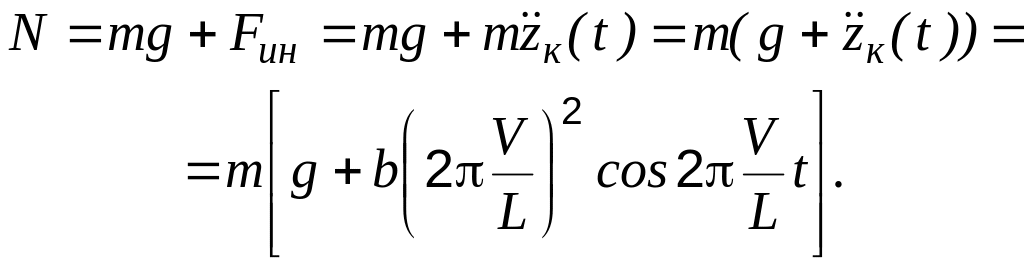(2.13)

Вывод: Из полученного выражения видно, что реакция воздействия колеса на путь будет зависеть от закона изменения неровности, а именно от параметров L и b, и скорости движения колеса.