
- •Основные задачи динамики локомотивов
- •Виды колебаний локомотивов
- •Возмущения, вызывающие колебания
- •Характеристики элементов соединений
- •Контрольные вопросы
- •Методика составления уравнений колебаний динамической модели экипажа
- •2.1. Принцип Даламбера
- •Динамическая модель экипажа
- •Составление уравнений вертикальных колебаний модели с одной степенью свободы при кинематическом возмущении
- •Контрольные вопросы
- •Составление уравнений вертикальных колебаний упрощенных динамических моделей
- •Уравнение колебаний модели с одной степенью свободы при силовом возмущении
- •Уравнения колебаний модели плоского двухосного экипажа
- •Контрольные вопросы
- •Свободные колебания динамических систем
- •4.1. Общие положения
- •4.2. Свободные колебания в недемпфированной системе
- •4.3. Свободные колебания в системе с гидравлическим гасителем
- •Контрольные вопросы
- •Матричная форма записи уравнений колебаний
- •5.1. Матричная форма записи уравнений колебаний в общем виде
- •5.2. Принцип составления уравнений колебаний в матричной форме на примере одноосной модели с двумя степенями свободы
- •Контрольные вопросы
- •Вынужденные колебания динамических систем
- •6.1. Понятие о возмущенном движении и методах исследования вынужденных колебаний
- •6.2. Частотный метод исследования вынужденных колебаний
- •6.3. Частотные характеристики модели с одной степенью свободы при кинематическом возмущении
- •Контрольные вопросы
- •Методика получения выражений амплитудных частотных (ачх) и фазовых частотных характеристик (фчх)
- •7.1. Преобразование чх системы с одной степенью свободы при кинематическом возмущении
- •7.2. Ачх и фчх системы с одной степенью свободы
- •7.3. Анализ ачх и фчх обобщенных координат
- •7.4. Чх динамической системы при силовом возмущении
- •Контрольные вопросы
- •Колебания при случайных возмущениях
- •8.1. Характеристики стационарных случайных процессов
- •8.2. Статистические характеристики случайного возмущения
- •8.3. Расчет показателей динамических качеств экипажной части
- •Контрольные вопросы
- •Боковые колебания локомотивов
- •9.1. Кинематическое описание процесса качения колесной пары по рельсам
- •Контрольные вопросы
Боковые колебания локомотивов
РЕКОМЕНДОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК
[1, гл. 5 § 5.1, § 5.2]
[2, гл. 3, п.п. 3.6]
[4, гл. 5, п.п. 5.4]
Рассматриваемые вопросы:
Кинематическое описание процесса качения колесной пары по рельсам;
Качение колесной пары без скольжения;
Качение колесной пары со скольжением.
9.1. Кинематическое описание процесса качения колесной пары по рельсам
9.1.1. Общие положения
Известно,
что поверхности катания бандажей
выполняют конусными. Вследствие этого
процесс качения колесной пары по рельсам
при смещении относительно оси пути
сопровождается извилистым движением,
состоящим из колебаний относа
![]() и виляния
и виляния
![]() .
Этот процесс кинематически может
осуществляться двумя способами: чистым
качением (качение без проскальзывания
в точках контакта колеса и рельса) и
качением со скольжением вдоль и поперек
пути.
.
Этот процесс кинематически может
осуществляться двумя способами: чистым
качением (качение без проскальзывания
в точках контакта колеса и рельса) и
качением со скольжением вдоль и поперек
пути.
Условия, при которых возникает один из этих видов движения, зависят от сил, приложенных к колесной паре, ее инерционных характеристик и физических явлений в точке контакта колес с рельсами. Рассмотрим вначале кинематические зависимости, характеризующие оба эти вида движения.
Рисунок
9.1. Скорости в точке контакта колеса и
рельса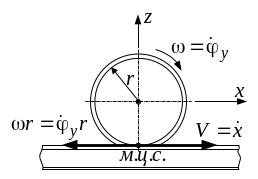
![]() вдоль пути, будет катиться прямолинейно
с угловой скоростью
вдоль пути, будет катиться прямолинейно
с угловой скоростью
![]() ,
так как мгновенный центр скоростей
колеса расположен в точке контакта с
рельсом (рис. 9.1.). В этом случае уравнение
кинематической связи, устанавливающей
условие чистого качения, имеет вид:
,
так как мгновенный центр скоростей
колеса расположен в точке контакта с
рельсом (рис. 9.1.). В этом случае уравнение
кинематической связи, устанавливающей
условие чистого качения, имеет вид:
![]() .
(9.1)
.
(9.1)
Оно выражает равенство нулю абсолютной скорости точки контакта колеса и рельса.
9.1.2. Качение колесной пары без скольжения
Особенность движения колесной пары в режиме качения без проскальзывания состоит в том, что ее извилистое движение возникает не под действием восстанавливающих сил, а вследствие свойств наложенных кинематических связей.
Рисунок
9.2. Изменение радиуса круга катания
колес при извилистом движении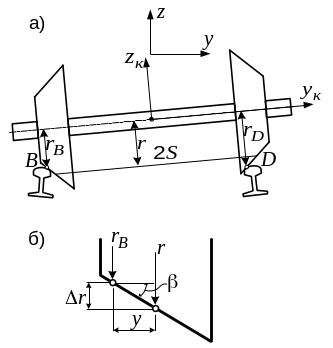
![]() сообщить колесной паре малое возмущение
– поперечное
и (или) угловое
,
сохранив при этом условие качения без
скольжения, то колесная пара будет
катиться по рельсам, одновременно
совершая извилистое движение, вследствие
того, что при отклонении поперек оси
пути радиусы колес станут разными (рис.
9.2а). Радиусы колес определяются
выражением:
сообщить колесной паре малое возмущение
– поперечное
и (или) угловое
,
сохранив при этом условие качения без
скольжения, то колесная пара будет
катиться по рельсам, одновременно
совершая извилистое движение, вследствие
того, что при отклонении поперек оси
пути радиусы колес станут разными (рис.
9.2а). Радиусы колес определяются
выражением:
![]() ,
(9.2)
,
(9.2)
где
![]() - величина изменения радиуса за счет
конусности, которая определяется (см.
рис. 9.2б) выражением:
- величина изменения радиуса за счет
конусности, которая определяется (см.
рис. 9.2б) выражением:
![]() ,
(9.3)
,
(9.3)
где
![]() - величина поперечного смещения колесной
пары;
- уклон (конусность) конической части
бандажа.
- величина поперечного смещения колесной
пары;
- уклон (конусность) конической части
бандажа.
Рисунок
9.3. Проекции скоростей в точках контакта
колес и рельсов 2S
– расстояние между кругами катания
колес колесной пары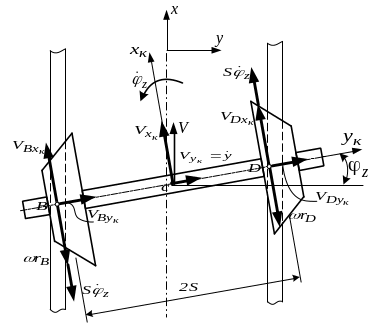
![]() так, что в точке касания
так, что в точке касания
![]() скорость
скорость
![]() направлена против скорости
,
а в точке
направлена против скорости
,
а в точке
![]() по направлению
(рис. 9.3).
по направлению
(рис. 9.3).
Условие малости угла будет иметь вид:
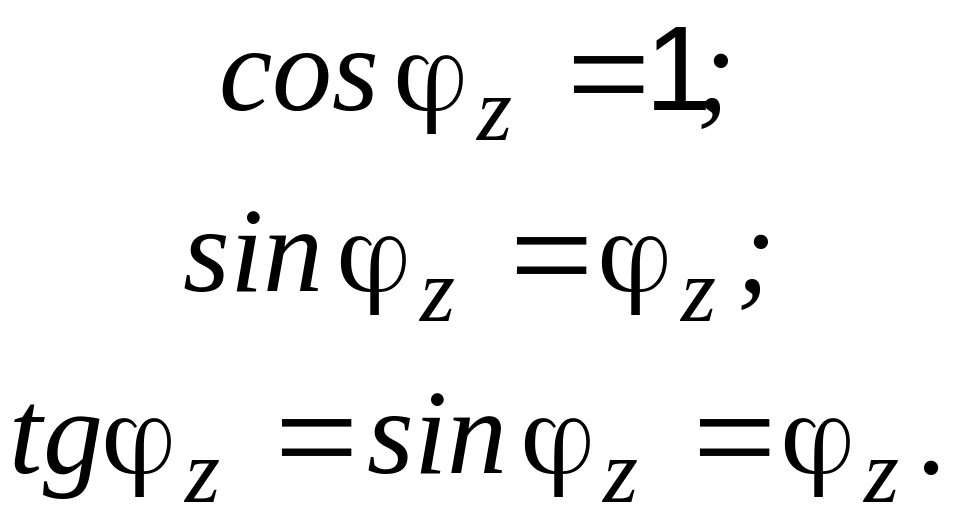 (9.4)
(9.4)
Условие качения без скольжения запишем в следующем виде:
![]() (9.5)
(9.5)
Выразим абсолютную
скорость в точке
в направлении, перпендикулярном оси
колесной пары (оси
![]() ),
и приравняем ее нулю:
),
и приравняем ее нулю:
![]() (9.6)
(9.6)
С учетом формул 9.2, 9.3 и 9.4 выражение примет следующий вид:
![]() (9.7)
(9.7)
Окончательно будем иметь:
![]() (9.8)
(9.8)
Условие качения без скольжения в точке приводит к аналогичным результатам, но со знаком “минус”:
![]() (9.9)
(9.9)
Запишем выражение для
проекций скоростей тех же точек на ось
![]() колесной пары. Эти проекции будут
одинаковы для любой точки колесной пары
и определяются выражениями:
колесной пары. Эти проекции будут
одинаковы для любой точки колесной пары
и определяются выражениями:
![]() (9.10)
(9.10)
Таким образом, при
качении колесной пары по рельсам без
скольжения ее обобщенные координаты и
скорости (
,
![]() ,
,
![]() ,
),
кроме уравнения 9.1 должны удовлетворять
еще двум уравнениям связи:
,
),
кроме уравнения 9.1 должны удовлетворять
еще двум уравнениям связи:
![]() (9.11)
(9.11)
Найдем решение этих уравнений, для этого продифференцируем второе уравнение в системе (9.11) и подставим в него из первого уравнения:
![]() (9.12)
(9.12)
Это уравнение описывает
гармонические колебания с частотой
![]() .
Период колебаний определяется выражением:
.
Период колебаний определяется выражением:
![]() .
(9.13)
.
(9.13)
То есть при отклонении колесная пара совершает гармонические колебания относа от среднего положения.
Одновременно с этим согласно второму уравнению системы (9.11) происходят колебания виляния:
![]() .
(9.14)
.
(9.14)
Решение уравнения (9.12) (закон колебаний относа) имеет вид:
![]() .
(9.15)
.
(9.15)
Закон колебаний виляния согласно уравнению (9.14) будет иметь вид:
![]() (9.16)
(9.16)
Сравнивая выражения
(9.15) и (9.16), видим, что при чистом качении
вдоль пути колесная пара совершает
извилистое движение относа и виляния
с одинаковой частотой
![]() и со сдвигом по фазе на 90о.
Длина волны относа или виляния определяется
следующим выражением:
и со сдвигом по фазе на 90о.
Длина волны относа или виляния определяется
следующим выражением:
![]() .
(9.17)
.
(9.17)
Из полученного выражения
видно, что
![]() не зависит от скорости
,
а зависит только от параметров колесной
пары и пути (
не зависит от скорости
,
а зависит только от параметров колесной
пары и пути (![]() ,
и
,
и
![]() ).
).
Для неизношенного
конусного бандажа
![]() ,
принимая
,
принимая
![]() м, получим
м, получим
![]() м. Для колеса электровоза ВЛ80 с
м. Для колеса электровоза ВЛ80 с
![]() м имеем
м имеем
![]() м.
м.
Выводы:
Для снижения интенсивности извилистого движения подвижного состава (колебаний виляния) необходимо уменьшать его амплитуду (максимальная амплитуда траектории извилистого движения равна половине суммарного зазора между головками рельсов и гребнями) за счет уменьшения ширины колеи (от 1524 до 152 мм).
Законы колебаний (9.15) и (9.16) описывают чисто кинематические связи. Характеристики этих колебаний зависят только от начальных условий и не связаны с действующими силами и инерционными параметрами колесной пары. Это условие выполняется при низких скоростях. С ростом скорости увеличивается , что ведет к росту инерционных сил и повышает вероятность проскальзывания колеса по рельсу.
Режим качения без скольжения, при котором скорости точек контакта колеса и рельса одинаковы, возможен лишь при условии – абсолютной твердости контактирующих тел. Если рассматривать реальную колесную пару и рельс, то в месте контакта всегда возникают деформации. Однако поскольку эти деформации малы, то некоторые характеристики движения под действием возмущений при учете деформаций могут быть близки к аналогичным без деформаций, то есть при небольших скоростях движения.
9.1.3. Качение колесной пары со скольжением
При качении колесной пары со скольжением обобщенные координаты и не обязательно изменяются по гармоническому закону, скорости в точках и контакта колес с рельсами не равны нулю и скорости проскальзывания на основе ранее полученных соотношений определяются:
![]() (9.18)
(9.18)
![]() .
(9.19)
.
(9.19)
Результаты теоретических исследований показывают, что силы взаимодействия деформируемых колес и рельсов могут быть выражены через относительные скорости проскальзывания, которые находят как частное от деления скоростей проскальзывания на скорость движения. Относительные скорости проскальзывания определяются выражениями:
![]() (9.20)
(9.20)
![]() .
(9.21)
.
(9.21)
Эти соотношения в дальнейшем будут использованы для определения сил реакций рельсов на колесную пару.
