8.2. Статистические характеристики случайного возмущения

Определение характеристик колебаний динамической системы при случайном возмущении относится к задачам вынужденных колебаний. Для исследования вынужденных колебаний необходимо располагать характеристиками неровностей пути, выступающих в роли возмущения.

Многочисленные работы, проведенные в России и за рубежом в области изучения неровностей пути, показывают, что они носят сложный характер и имеют в своем составе как периодические составляющие, кратные по длине рельсовому звену, так и случайные составляющие с широким спектром частот.

В связи с этим непостоянство свойств пути по длине практически эквивалентно некоторой случайной геометрической неровности. Все это позволяет в качестве возмущающей функции принять некоторую эквивалентную геометрическую неровность, которая приближенно учитывает все причины, вызывающие появления колебаний ПС.

До последнего времени в качестве возмущения использовали детерминированные усредненные геометрические неровности, обусловленные просадкой стыков. На основе экспериментов Н.Н. Кудрявцева эти неровности подразделяют на одно- и двугорбые, период которых определяется длиной рельсового звена, т.е. 12,5 и 25 м. Наиболее часто при расчетах применяли одногорбую неровность, описываемую уравнением

, (8.9)

где - амплитуда неровности, ( мм – для пути в хорошем состоянии, мм – для пути в удовлетворительном состоянии);

- круговая частота, ; - скорость движения; - длина волны неровности.

Однако, модели, применяемые для описания колебательных процессов в локомотиве, должны обеспечивать возможность получения достаточно точных результатов, т.е., колебательные процессы, определенные в результате расчета на моделях, должны быть близки к результатам эксперимента на движущемся локомотиве.

Поэтому статистические характеристики эквивалентной геометрической неровности получают экспериментально при записи ускорений букс колесных пар или их абсолютных перемещений (перемещений букс относительно земли).

В течение ряда лет производилась статистическая обработка экспериментальных данных с целью определения некоторых эталонных спектральных характеристик эквивалентной геометрической неровности. Получено следующее аналитическое выражение спектральной плотности для частотного диапазона от 0 до 10 Гц [1]

, (8.10)

где - скорость движения, м/с; - частота, Гц; , , , , - параметры, значения которых приведены в таблице 8.1.

Таблица 8.1 – Значения параметров для скорости м/с

Номер cоставляющей	Значения параметров		Номер cоставляющей	Значения параметров
				, мм2	, м-1	, м-1
1	0,0055	3,1915	1	2,3816	0,0424	0,0031
2	9,9112	0,9892	2	2,2118	0,0822	0,0026
3	0,0125	4,1027	3	1,0591	0,1216	0,0052
-	-	-	4	0,4047	0,1658	0,0031

Номер составляющей назначается в соответствии со следующим условием, если , то ; если , то ; если , то , где и определяются по формулам

, (8.11)

, (8.12)

В соответствии с формулой (8.10) спектр состоит из монотонно убывающей по гиперболическому закону составляющей, на которую наложены отдельные пики (рис. 8.3).

Рисунок 8.3 Спектральная плотность эквивалентной геометрической неровности при скорости движения м/с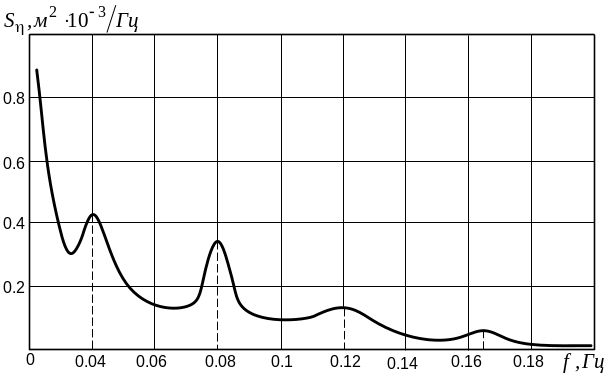

В соответствии с физическими представлениями ординаты резко уменьшаются с ростом частоты так как неровности большей длины имеют и большую амплитуду. Из рисунка 8.3 видно, что на графике имеется несколько максимумов, обусловленных неоднородностью свойств пути в зоне стыков или в местах сварки рельсов. Так, первый максимум соответствует частоте 0,04 Гц или неровности м, т.е. длине рельсового звена.

Два других максимума объясняются специфическими процессами, возникающими в системе, при воздействии на нее последовательности периодически повторяющихся импульсов. В нашем случае такие импульсы возникают при проходе болтовых или сварных стыковых соединений. В механике доказано, что в отличие от непрерывно действующего возмущения, при котором возникает один резонанс, воздействие периодически повторяющихся импульсов вызывает резонансы не только на основной частоте их повторения, но и на кратных частотах. Этим явлением объясняется наличие двух последующих максимумов на частотах 0,08 Гц и 0,12 Гц, соответствующих длинам неровности 12,5 м и 8,3 м.

Отметим еще две особенности спектральной плотности возмущения. Естественно, что при , амплитуда неровности неограниченно возрастает, т.е. график нельзя строить от нуля. Начальное значение в зависимости от скорости движения принимают соответствующим от 30 до 100 м.

Начиная с частоты Гц амплитуда неровности убывает почти по экспоненциальному закону, т.е. высокочастотные неровности вносят малый вклад в низкочастотные колебания подрессоренных частей локомотивов.

Для диапазона частот от 10 до 100 Гц спектральная плотность эквивалентной неровности зависит от нагрузки на ось исследуемого локомотива

, (8.13)

где - нагрузка на ось, кН.

Скорость движения в формулу (8.13) подставляется в км/ч, а размерность получается в см²/Гц.

Используя выражения (8.10), (8.13) и АЧХ динамической системы по формуле (8.8) можно найти спектральную плотность выходных координат линейной динамической системы (для данного примера – вертикального перемещения ). Аналитические выражения спектральных плотностей (формулы 8.10 и 8.13) позволяют моделировать случайные возмущения в области частот до 100 Гц, поэтому они могут быть использованы при исследовании показателей вертикальных колебаний подрессоренных масс локомотивов.