Контрольные вопросы

1. Как выполняется преобразование ЧХ?

2. Как получить АЧХ и ФЧХ динамической системы?

3. Что показывают АЧХ и ФЧХ?

4. Чем определяется размерность АЧХ и ФЧХ?

5. Как изменяется АЧХ при увеличении частоты возмущений?

6. Как влияет относительное демпфирование на АЧХ?

7. Что такое резонанс?

8. Как влияет величина жесткости на силы в рессорном подвешивании?

9. Как получить ЧХ системы при силовом возмущении?

10. В чем основное отличие ЧХ при силовом возмущении и кинематическом?

11. Как выбирают жесткость виброзащитных элементов силового оборудования локомотива?

8. Колебания при случайных возмущениях

РЕКОМЕНДОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК

[1, гл. 2 § 2.6, гл. 4 § 4.2]

[2, гл. 3, п.п. 3.3.2]

[4, гл. 1, п.п. 1.7]

Рассматриваемые вопросы:

1. Характеристики стационарных случайных процессов;

2. Статистические характеристики случайного возмущения;

3. Расчет показателей динамических качеств экипажной части.

8.1. Характеристики стационарных случайных процессов

Возмущения, вызывающие колебания ПС, являются случайными. Это объясняется тем, что колебания вызываются множеством факторов, которые в большинстве случаев носят случайный характер (неровности на поверхности рельсов и бандажей, жесткость рельсового пути). Анализ фактических записей неровности рельсового пути показывает, что они носят случайный и непрерывный характер и аналитическое их описание возможно лишь с помощью теории случайных процессов. Случайным процессом называется бесконечная совокупность функций времени, значения которых в произвольный момент времени могут быть любыми. Отдельная функция времени из этой совокупности представляет собой реализацию случайного процесса (графическое изображение).

Рассмотрим три реализации случайного процесса (рис. 8.1). Главное отличие реализаций, показанных на рисунке 8.1, заключается в том, что при их наложении они не совпадают. Большое значение при исследовании случайных колебаний имеет правильный выбор длины реализации. Результаты испытаний свидетельствую о том, что удержать постоянную скорость локомотива более 30 секунд невозможно. Поэтому в расчетах принимают время реализации .

Рисунок 8.1. Реализации случайного процесса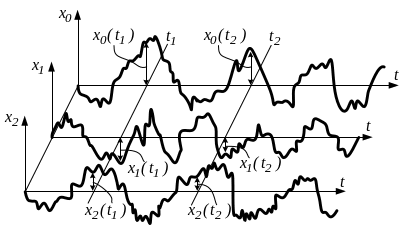

На практике часто встречаются случайные процессы, протекающие во времени приблизительно однородно и имеющие вид непрерывных случайных колебаний вокруг некоторого среднего значения, причем ни средняя амплитуда, ни характер этих колебаний не меняется существенно с течением времени. Такие случайные процессы называются стационарными. В каждый момент времени значения реализаций можно рассматривать как совокупность значений случайных величин . Для описания этих совокупностей используются следующие неслучайные функции:

1. Математическое ожидание случайной функции 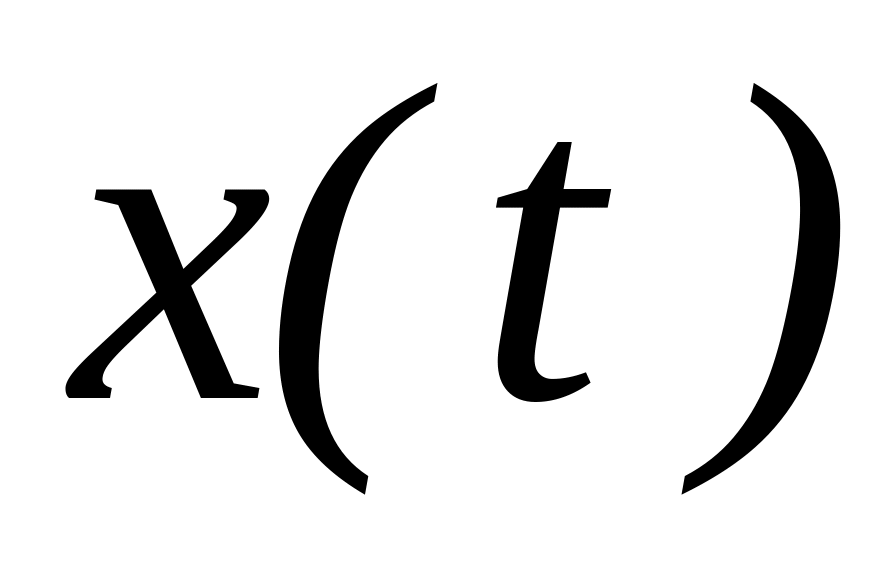- неслучайная функция 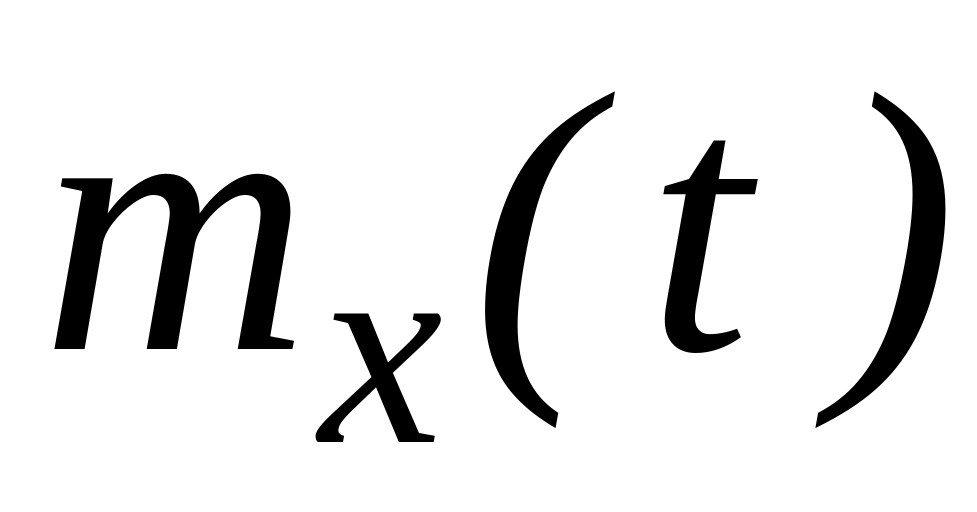, которая при каждом значении аргумента равна математическому ожиданию соответствующего сечения совокупности случайных функций

. (8.1)

По смыслу математическое ожидание случайной функции есть некоторая средняя функция, около которой различным образом располагаются конкретные реализации случайной функции.

2. Десперсией случайной функции называется неслучайная функция 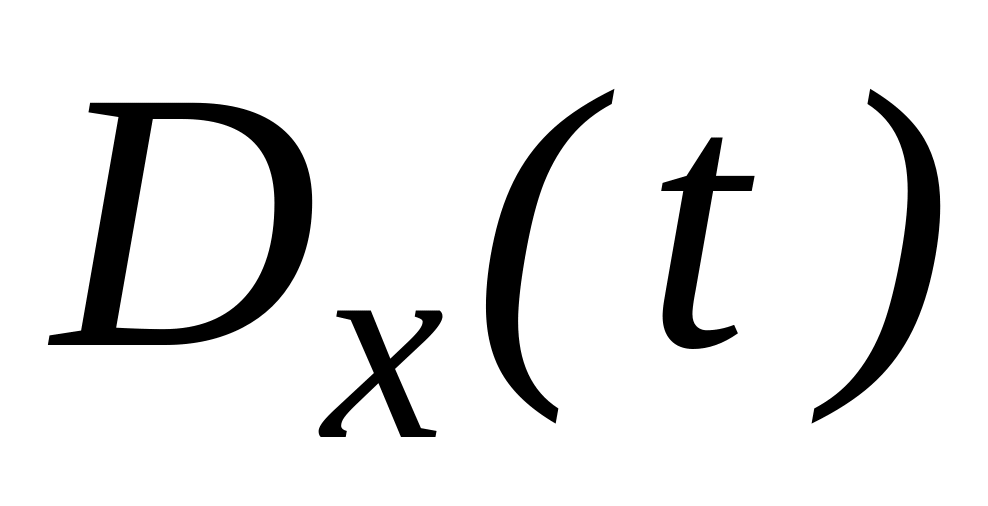, значение которой для каждого 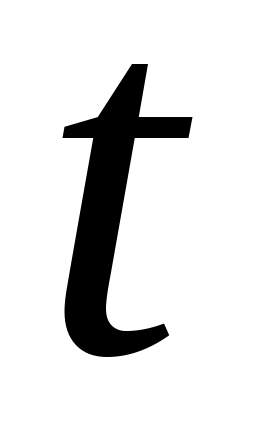равно дисперсии соответствующего сечения совокупности случайных функций

. (8.2)

Дисперсия случайной функции при каждом характеризует разброс (рассеяние случайной величины) возможных реализаций случайной функции относительно среднего, иными словами, “степени случайности” случайной функции.

3. Среднеквадратическое отклонение случайной функции 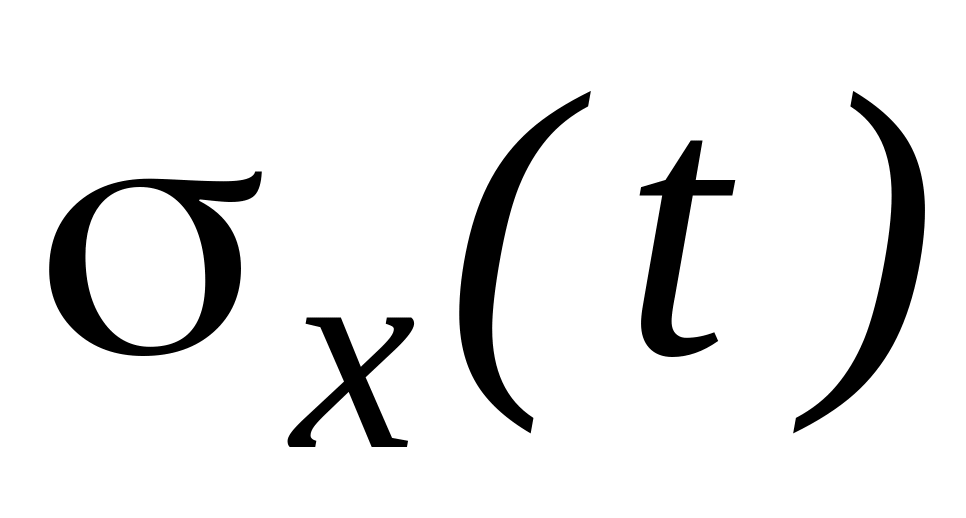- квадратный корень из дисперсии

. (8.3)

4. 

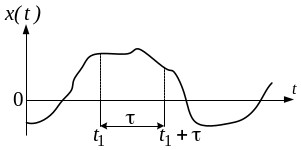
   Рисунок 8.2. Случайная функция

   Корреляционная функция характеризует степень зависимости между сечениями случайной функции, относящимися к различным моментам времени (рис. 8.2). Корреляционной функцией случайной функции называется неслучайная функция двух аргументов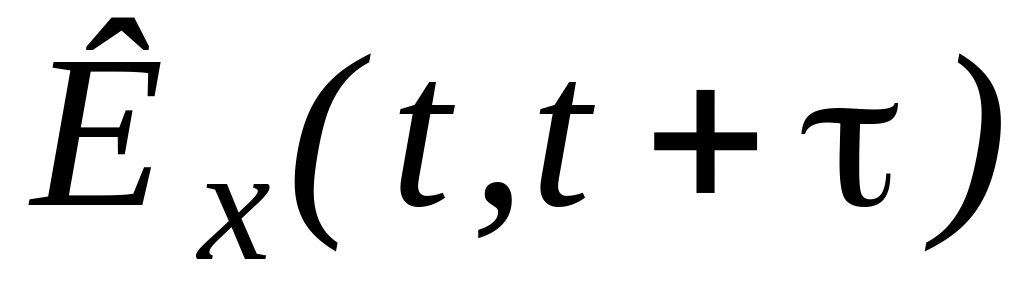 , которая при каждой паре значений 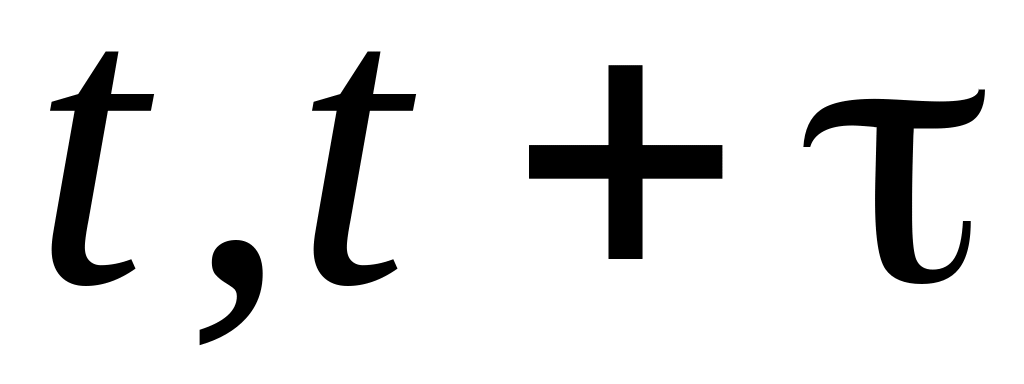равна корреляционному моменту соответствующих сечений случайной функции:

, (8.4)

где - центрированная случайная функция, определяемая как

(8.5)

При корреляционная функция обращается в дисперсию случайной функции, т.е.

, (8.6)

5. Если какой либо колебательный процесс представляется в виде суммы гармонических колебаний различных частот (так называемых “гармоник”), то функция, описывающая распределение амплитуд по различным частотам называется спектром колебательного процесса. Спектр показывает, какого рода колебания преобладают в данном процессе, какова его внутренняя структура. Совершенно аналогичное спектральное описание можно дать и стационарному случайному процессу, вся разница в том, что для случайного процесса амплитуды колебаний будут случайными величинами. Спектр стационарной функции будет описывать распределение дисперсий по разным частотам. Распределение такого рода называется спектральным разложением стационарной случайной функции.

Характеристика, описывающая частотный состав стационарного процесса, называется спектральной плотностью

. (8.7)

Размерность спектральной плотности равна квадрату размерности случайного процесса, умноженной на секунду. В соответствии с этим физический смысл спектральной плотности состоит в том, что она характеризует распределение энергии случайного процесса по частотам спектра.

Возмущения, возникающие при движении железнодорожного экипажа по рельсовому пути, являются случайными. Колебания подрессоренных масс экипажа, движущегося по случайным неровностям рельсового пути, также представляют собой стационарный случайный процесс. Статистические характеристики этого процесса могут быть установлены по статистическим характеристикам входного возмущения и АЧХ динамической системы.

Спектральная плотность выходных координат линейной динамической системы определяется по формуле

, (8.8)

где - спектральная плотность входного возмущения;

- АЧХ динамической системы, связывающая возмущение и выходные координаты.