7.3. Анализ ачх и фчх обобщенных координат

Рисунок 7.1. АЧХ и ФЧХ вертикальных перемещений модели с одной степенью свободы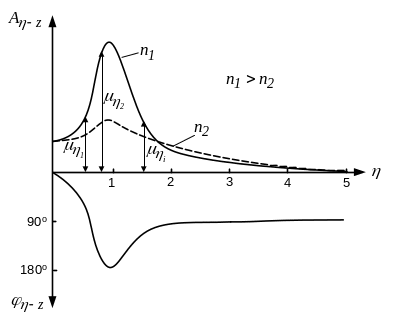

Рассмотрим, как изменяется от частоты возмущения амплитуда колебаний модели локомотива с одной степенью свободы, т.е. АЧХ (формула 7.13). Анализ будем выполнять, пользуясь безразмерной частотой . Графики АЧХ и ФЧХ для перемещений имеют вид, показанный на рисунке 7.1. При увеличении частоты возмущений или числитель АЧХ (см. формулу 7.13) возрастает, а знаменатель сначала убывает и при равен , а затем начинает возрастать.

Таким образом, амплитуда неровности будет передаваться на кузов увеличенной в раз.

АЧХ так же зависит от относительного демпфирования , соотношения частот вынужденных и собственных колебаний и имеет максимум на частоте близкой к (резонанс), т.е. к частоте собственных колебаний .

Резонанс – совпадение частот вынужденных и собственных колебаний.

Увеличение приводит к тому, что в резонансной зоне амплитуда будет уменьшаться, а в зарезонансной увеличиваться. Так как динамические качества локомотива определяются не только перемещениями, но и ускорениями и силами в рессорном подвешивании, то запишем АЧХ для ускорений и сил, используя при этом характеристики связей

, (7.17)

. (7.18)

Таким образом, АЧХ перемещений, ускорений и сил одинаково зависят от частоты и отличаются только множителями. Преобразовав выражения (7.17) и (7.18) можно показать, что ускорения и силы будут пропорциональны жесткости рессорного подвешивания

. (7.19)

. (7.20)

Это соответствует установившимся представлениям, что для улучшения динамических качеств локомотивов следует снижать жесткость рессорного подвешивания.

Рисунок 7.2. АЧХ вертикальных ускорений модели с одной степенью свободы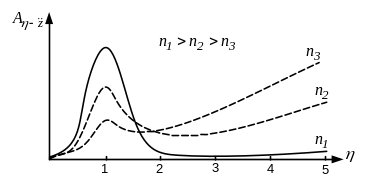

Влияние коэффициента демпфирования или относительного затухания на АЧХ не так однозначно как жесткости. АЧХ ускорений системы с одной степенью свободы показана на рисунке 7.2. Как видно из рисунка увеличение приводит к уменьшению амплитуды на резонансной частоте, однако в зарезонансной зоне увеличение приводит к значительному увеличению амплитуды, а следовательно ускорений и сил в рессорном подвешивании.

7.4. Чх динамической системы при силовом возмущении

При расчете виброзащиты от силовых возмущений, связанных с вращением неуравновешенных частей, также можно использовать модель с одной степенью свободы. ЧХ перемещений в такой модели получим, используя уравнение колебаний (см. формулу 3.4) и переходя из временной области в частотную, получим

. (7.21)

Сравнивая полученное выражение при силовом возмущении и аналогичное ранее полученное при кинематическом возмущении (см. формулу 6.13), можно сделать вывод, что левые части этих выражений одинаковы, а правые различны. Поэтому динамические свойства также будут различны.

ЧХ будет иметь следующий вид

. (7.22)

Выражение (7.21) можно записать в виде

. (7.23)

Для задач виброзащиты силового оборудования локомотивов (дизель - генераторные установки, мотор - компрессоры и т.д.) частота силового возмущения зафиксирована, как правило, в определенном диапазоне. Поэтому во избежании резонанса, жесткости виброзащитных элементов в таких случаях выбирают большими, так, чтобы собственная частота системы значительно превосходила рабочие частоты. Здесь влияние жесткости на динамические свойства противоположно ее влиянию в схемах с кинематическим характером возмущения.