7. Методика получения выражений амплитудных частотных (ачх) и фазовых частотных характеристик (фчх)

РЕКОМЕНДОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК

[1, гл. 2 § 2.4, гл.4 § 4.1]

[2, гл. 3, п.п. 3.3]

[7, гл. 2, п.п. 2.2]

Рассматриваемые вопросы:

1. Преобразование ЧХ системы с одной степенью свободы при кинематическом возмущении;

2. АЧХ и ФЧХ системы с одной степенью свободы;

3. Анализ АЧХ и ФЧХ обобщенных координат;

4. ЧХ динамической системы при силовом возмущении.

7.1. Преобразование чх системы с одной степенью свободы при кинематическом возмущении

Имея выражение ЧХ в комплексной форме можно в дальнейшем получить формулы для амплитудной частотной характеристики (АЧХ) и фазовой частотной характеристики (ФЧХ) динамической системы. Для этого необходимо отделить вещественные части от мнимых в выражениях ЧХ.

Так как в полученных ранее выражениях ЧХ (формулы 6.14, 6.18, 6.19, 6.22, 6.25) знаменатели одинаковы, а в числителях прослеживается присутствие некоторых аналогичных выражений можно выполнить преобразования, приводящие ЧХ к более компактному виду.

Для примера рассмотрим преобразование выражения ЧХ динамической модели с одной степенью свободы (формула 6.14). Для этого введем два параметра, характеризующие колебательные свойства рассматриваемой системы, а именно – собственную частоту недемпфированной системы (гл.4, формула 4.2) и относительный коэффициент затухания n (гл.4, формула 4.7).

Преобразуем выражение ЧХ (формула 6.14), разделив числитель и знаменатель на жесткость , получим

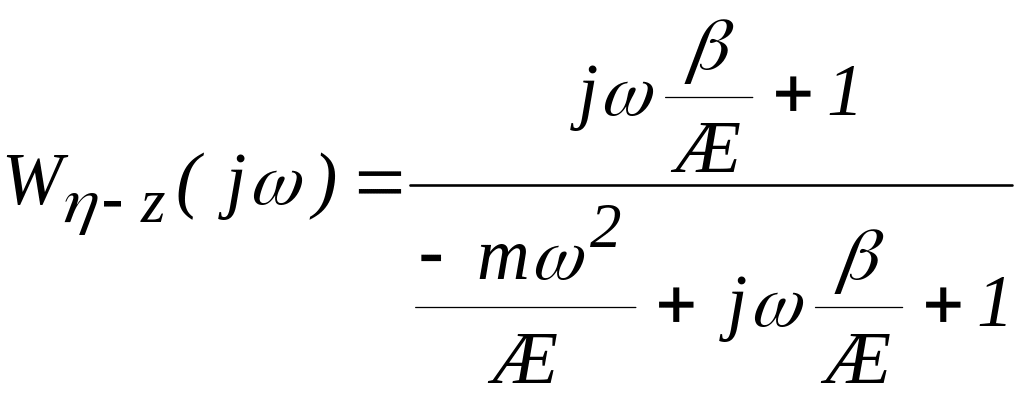. (7.1)

Из выражения 4.7 выразим и подставим в (7.1)

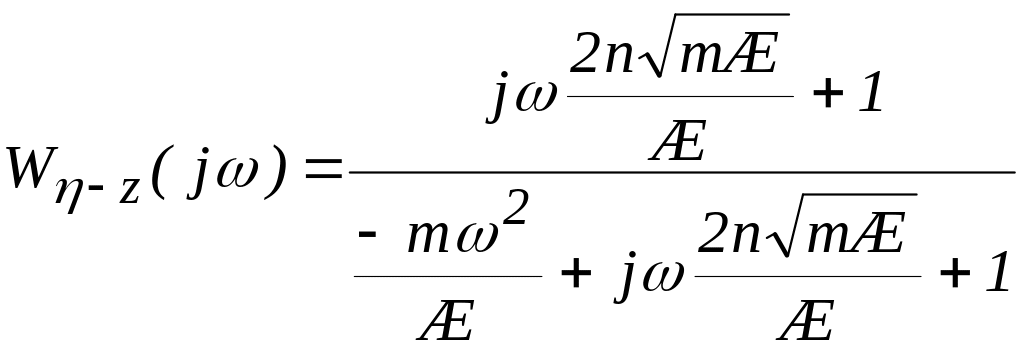. (7.2)

Введем в это выражение , после преобразования получим

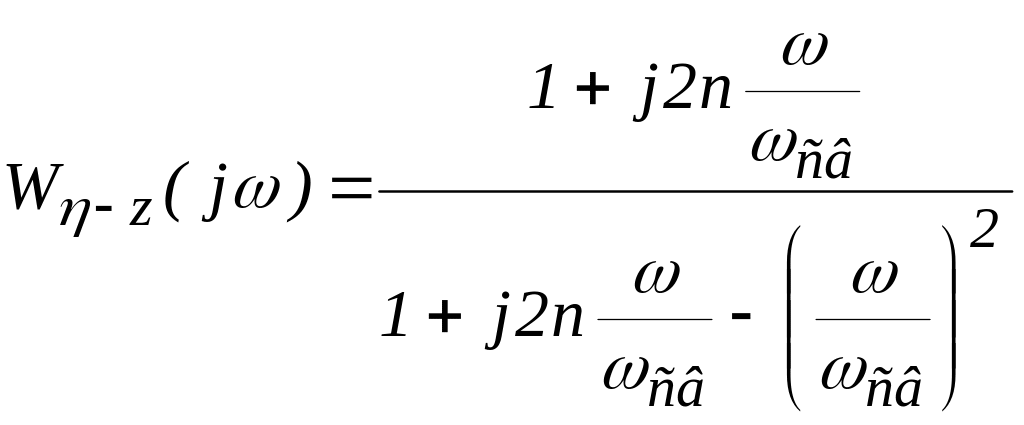. (7.3)

Используя полученное упрощенное выражение ЧХ для координаты , можно получить упрощенную ЧХ для остальных координат ( , , , и ) используя при этом соответствующие ЧХ связей (гл.6, формулы 6.16, 6.17).

Преобразованные ЧХ используются для нахождения АЧХ и ФЧХ динамической системы, позволяющих проанализировать динамические свойства.

7.2. Ачх и фчх системы с одной степенью свободы

Построение графиков ЧХ необходимо производить на комплексной плоскости, что при теряет наглядность. Поэтому для получения АЧХ и ФЧХ необходимо использовать соответствующую ЧХ, преобразовав ее таким образом, чтобы в числителе и знаменателе содержалось по одному комплексному числу с явно выраженной действительной и мнимой частью.

Известно, что комплексную функцию можно представить в показательной форме

, (7.4)

где - действительная часть ЧХ;

- мнимая часть ЧХ;

- модуль ЧХ или амплитудная частотная характеристика (АЧХ);

- фазовая частотная характеристика (ФЧХ).

Функции и рассчитываются по формулам

, (7.5)

. (7.6)

Характеристики АЧХ и ФЧХ можно построить в обычных координатах и по построенным графикам анализировать динамические свойства системы.

Рассмотрим для примера методику получения АЧХ и ФЧХ системы с одной степенью свободы при кинематическом возмущении для выходной координаты (вертикальное перемещение массы m). Преобразованная ЧХ для этого случая представлена формулой (7.3). Для получения АЧХ и ФЧХ необходимо выражение (7.3) привести к виду

. (7.7)

Для рассматриваемого случая имеем

действительная часть

, (7.8)

, (7.9)

мнимая часть

, (7.10)

. (7.11)

Для получения АЧХ с учетом формул (7.5) и (7.7) имеем

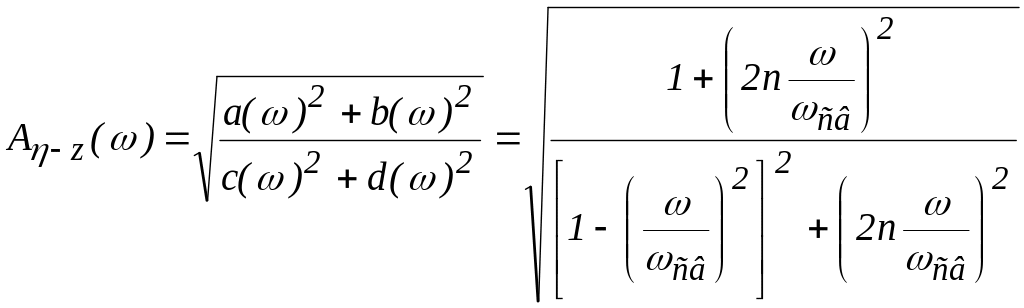. (7.12)

Упростим полученное выражение АЧХ, заменив на

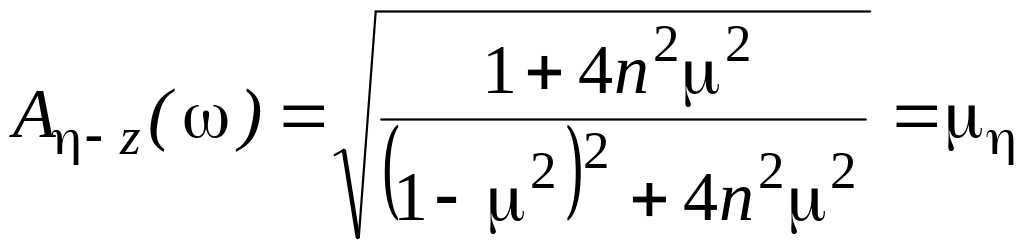. (7.13)

где - безразмерная частота;

- динамический коэффициент.

АЧХ показывает, как динамическая система преобразует амплитуду входного воздействия (возмущения).

Для получения ФЧХ используем выражения (7.6) и (7.7). Найдем фазу числителя выражения (7.7)

, (7.14)

и фазу знаменателя

. (7.15)

ФЧХ будет иметь вид

. (7.16)

ФЧХ показывает, как динамическая система преобразует фазу входного воздействия.

АЧХ и ФЧХ имеют размерность. Размерность АЧХ определяется размерностью выходной координаты. ФЧХ измеряется либо в градусах, либо в радианах.