6.3. Частотные характеристики модели с одной степенью свободы при кинематическом возмущении

Рассмотрим в качестве примера получение ЧХ для модели с одной степенью свободы. Для получения ЧХ необходимо иметь уравнение колебаний, которое для данной модели имеет следующий вид (см. гл. 2, формула 2.19)

. (6.8)

Преобразуем уравнение в операторную форму. Для перехода из временной области в частотную используем следующие выражения

, (6.9)

, (6.10)

. (6.11)

В соответствии с (6.9), (6.10) и (6.11) уравнение (6.8) примет вид

. (6.12)

Вынесем за скобки постоянные множители, получим

. (6.13)

Для получения ЧХ необходимо многочлен правой части разделить на многочлен левой

. (6.14)

Выражение (6.14) представляет собой ЧХ, связывающую возмущение с обобщенной координатой (вертикальное перемещение z).

С учетом (6.14) уравнение (6.13) примет вид

. (6.15)

Рисунок 6.1 Структурная схема колебаний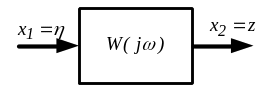

- входное воздействие;

- выходная координата.

ЧХ системы с одной степенью свободы можно показать в виде функциональной схемы, показанной на рисунке 6.1. Из приведенной схемы следует, что ЧХ системы показывает, каким образом динамическая система преобразует или входное возмущение. В обозначении ЧХ присутствуют два индекса и - . В качестве могут быть приняты абсолютные координаты (перемещения , скорости , ускорения ), а также относительные координаты (перемещения , скорости , ускорения ) и силы, возникающие в рессорном подвешивании.

ЧХ для всех указанных выходных координат получают с использованием ЧХ связей и ранее выведенной ЧХ .

Найдем соответствующие ЧХ системы, связывающие абсолютное перемещения массы с ее абсолютными скоростями и ускорениями

, (6.16)

. (6.17)

Для получения ЧХ, связывающих входную координату с выходными и , необходимо умножить ЧХ (формула 6.14) на соответствующую характеристику связи, получим

, (6.18)

. (6.19)

Для получения ЧХ относительных координат ( , и ) необходимо выразить относительное перемещение массы m через абсолютное перемещение и амплитуду неровности

. (6.20)

Заменив в этом выражении выражением (6.15) получим

. (6.21)

ЧХ, связывающая с выходной координатой имеет вид

. (6.22)

Получение ЧХ, связывающих входную координату с выходными и , выполняется аналогично как и для абсолютных координат.

Для получения ЧХ силы в рессорном подвешивании необходимо представить выражение этой силы. Сила в рессорном подвешивании определяется суммой упругих и диссипативных составляющих

. (6.23)

С учетом формул (1.1), (1.2) и (6.20) будем иметь

. (6.24)

Таким образом, выражение ЧХ для силы в рессорном подвешивании при кинематическом возмущении имеет вид

. (6.25)

Полученные ЧХ позволят исследовать свойства динамических систем, т.е. получить информацию об амплитуде и фазе колебаний.

Контрольные вопросы

1. Какие методы используют для нахождения обобщенных координат?

2. Какая основная цель частотного метода?

3. Каким образом находят ЧХ системы?

4. Что значит единичные возмущения?

5. Что показывает ЧХ динамической системы?

6. Как выполняют переход из временной области в частотную?

7. Какие параметры могут быть приняты в качестве выходной координаты при частотном методе исследования колебаний?

8. Для чего используются ЧХ связей и как их находят?

9. Каким образом получают ЧХ для силы в рессорном подвешивании?