Построение плана ускорений:

Определим ускорения звеньев механизма. По теореме о сложении ускорений можно записать:

, (3)

где – нормальное ускорение; ( – тангенциальное ускорение, т.к. );

– нормальное ускорение;

– кориолисово ускорение.

Таким образом, в уравнении (3) присутствуют два неизвестных по величине ускорения; для их вычисления воспользуемся методом векторных планов. Отложим от полюса плана ускорений π параллельно ОА отрезок πa₁, изображающий ускорение точки A кривошипа 1 (рис. 9). Для удобства вычислений длину этого отрезка примем равной 40 мм. Тогда масштаб плана ускорений .

Переведем в отрезки известные нам по величине ускорения:

– параллельно О₁А;

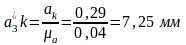– перпендикулярно к О₁А.

Так как отрезок π a^*₃ мал, пренебрежем его длиной, и будем считать, что точки π и a^*₃ совпадают. Направление отрезка , изображающего ускорение Кориолиса, определим, повернув отрезок , изображающий относительную скорость , (рис. 8) на 90⁰ в направлении вращения кулисы 3. Замыкая векторный многоугольник направлениями ускорений ( О₁А) и (//О₁А), в соответствии с уравнением (3) получим точку . Тогда отрезку будет соответствовать относительное ускорение , а отрезку – тангенциальное ускорение точки A, принадлежащей кулисе 3. Рассмотрим теперь движение суппорта 5 и кулисы 3. Согласно теореме о сложении ускорений имеем:

, (4)

где – ускорение суппорта 5,

– ускорение точки B кулисы 3 относительно точки B суппорта 5.

В данном случае , так как переносное движение суппорта – поступательное.

Нормальное ускорение:

,

отображающий это ускорение отрезок (//АВ).

Отрезок b^*₃b₃, отображающий тангенциальное ускорение ( АВ), найдем из соотношения:

.

Замыкая векторный многоугольник направлениями ускорений (//ОО) и ( ОО), в соответствии с уравнением (4) получим точку b₅ (рис. 9). Отрезок πb₅ отображает на плане ускорение суппорта 5. Длина этого отрезка – 55 мм, следовательно .

Таким образом, ускорение суппорта в положении механизма, изображенном на рис. 7, равно 2,20 м/c² и направлено в ту же сторону, что и вектор скорости суппорта. Это означает, что в данный момент времени суппорт ускоряется. Планы скоростей и ускорений, изображенные на рис. 8 и рис. 9 соответственно, дают полную информацию о скоростях и ускорениях звеньев механизма в заданном на рис. 7 положении. Для того чтобы получить векторные планы в другом положении механизма, необходимо заново выполнить все приведенные вычисления.

4. Пример выполнения задания

Исходные данные:

структурная схема механизма двигателя внутреннего сгорания;

N = 10;

h₀ = 0,09 м – базовый ход ползуна;

h = h₀ + 0,001N = 0,09 + 0,00110 = 0,1 м  ход ползуна;

V_ср = 4 м/с  средняя скорость ползуна;

 = l_OA /l_AB = 0,33  отношение длины кривошипа l_OA к длине шатуна l_AB;

₁ = 120^о  угол, определяющий положение начального звена ОА механизма в расчётном положении.