3.2.2.Одно уравнение с одним неизвестным

Для решения одного уравнения с одним неизвестным в пакете Mathcad используются функции и , где – функция, определенная где-либо в рабочем документе, или выражение, которое возвращает скалярное значение, – имя переменной, относительно которой ищется решение уравнения.

Функция требует дополнительного задания начального значения (guess value) переменной x. Для этого нужно просто предварительно присвоить x некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.

Если функция имеет несколько корней, то найденное значение корня будет зависеть от начального приближения для переменной x. Будет найдено такое значение корня, в окрестности которого задано начальное приближение.

Рассмотрим пример. Пусть необходимо найти все корни уравнения на отрезке .

Ниже приведен пример решения этого уравнения с применением функции . Для локализации корней используется построение графика функции на заданном интервале.

Иногда удобнее задавать не начальное приближение к корню, а интервал , внутри которого корень заведомо находится. В этом случае следует использовать функцию с четырьмя аргументами, а присваивать начальное значение не нужно, как показано ниже.

При использовании функции необходимо помнить следующее:

• внутри интервала не должно находиться более одного корня. Иначе будет заранее неизвестно, какой именно из корней найден;

• значения функций и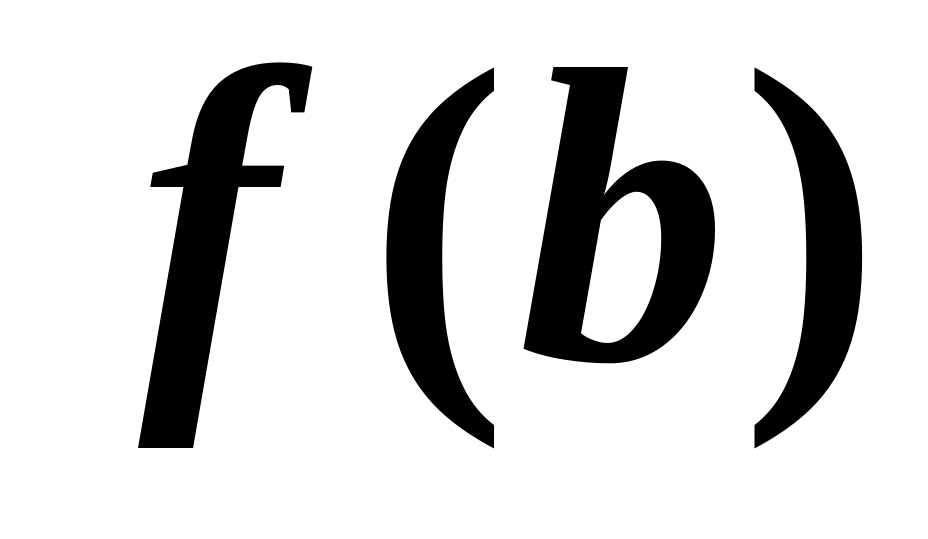 должны иметь разный знак, иначе будет выдано сообщение об ошибке.

Для нахождения корней полинома, т. е. для решения уравнения используется функция , где – вектор коэффициентов полинома. . Функция возвращает вектор, элементами которого являются корни полинома.

Пример. Найти все корни уравнения

Пример. Найти все корни уравнения

3.2.3.Системы нелинейных уравнений

Пусть необходимо решить систему уравнений

Процедура решения в пакете Mathcad имеет следующий вид:

• задаются начальные значения для всех переменных системы:

• Given – ключевое слово;

• записываются уравнения системы:

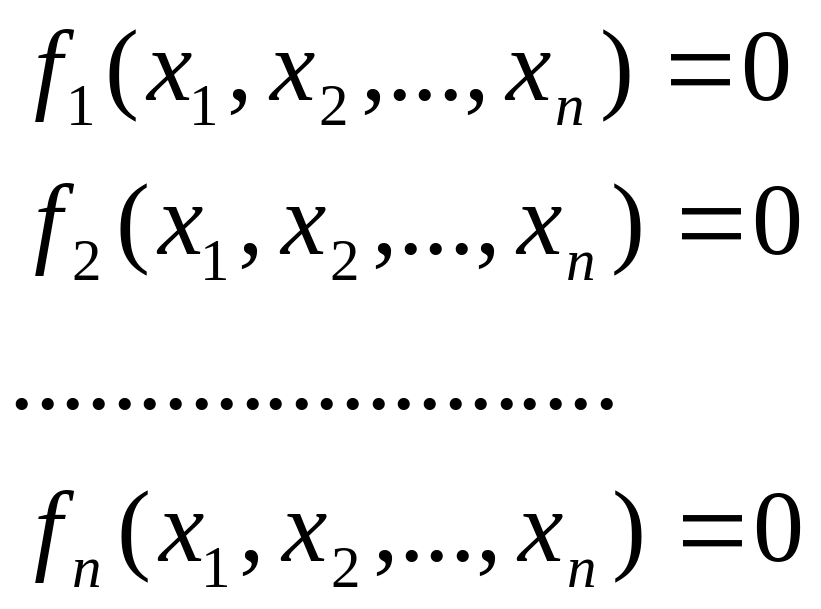
• находится решение системы уравнений в виде вектора значений соответствующих переменных.

Здесь – функция, которая возвращает решение системы уравнений в виде вектора значений соответствующих переменных, если оно существует.

При записи системы уравнений, после ключевого слова Given, при необходимости можно указывать ограничения на возможные значения переменных, используя символы , , и .

Замечание. При записи уравнений внутри блока Given…Find знак равенства следует вводить нажатием комбинаций клавиш <Ctrl>+<=> или использовать символ Equal to (логическое равенство) из палитры символов Boolean (Булево).

Если система уравнений является нелинейной, то найденное решение может быть не единственным и зависеть от начальных значений переменных.

Пример. Решить систему уравнений для :

Для поиска начальных приближений для переменных и выражаем из каждого уравнения как функцию и строим графики функций и .

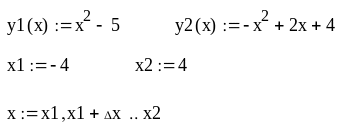
Находим первое решение:

Проверка найденного решения:

Находим второе решение:

Проверка найденного решения: