5. Вращательное движение. Кинематика вращательного движения.

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П , одна из которых неподвижна, а другая жестко связана с телом.

 φ=φ(t) – уравнение вращательного движения твердого тела.

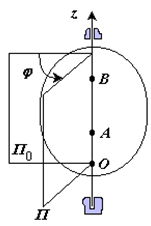
За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Кинематика вращательного движения твердого тела.

Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой – оси вращения.

1. Характеристики вращательного движения.

а) Угловая скорость .Быстрота вращения характеризуется угловой скоростью «омега», которая равна производной от угла поворота тела по времени . , (16)

- угол поворота тела за малое время .При равномерном вращении его быстроту также описывают частотой оборотов и периодом вращения . Частота оборотов равна числу оборотов, сделанных за единицу времени, , - число оборотов за время . Т.к. за один оборот тело поворачивается на угол, равный 2 , то и . Период вращения - это время, за которое тело совершает один оборот. Т.к. ,то . (19)

рад/с , об/с , с .

Рис.3.

б) Угловое ускорение .Угловое ускорение «эпсилон» равно производной от угловой скорости по времени , , - изменение угловой скорости за время . .

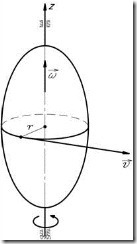
Векторы и направлены по оси вращения тела; вектор угловой скорости направлен в сторону хода правого винта при вращении винта в направлении вращения тела (рис.3). При ускоренном вращении тела направления векторов и совпадают, при замедленном – противоположны.

2. Связь линейных и угловых характеристик.Если точка тела отстоит от оси вращения на расстоянии , то за время она проходит путь .Скорость точки , или . При вращении тела тангенциальное ускорение его точки , или . Нормальное ускорение точки тела , или . (23)

Полное ускорение, как указывалось ранее, определяют по формуле .

3. Формулы равноускоренного вращения.

Если угловое ускорение постоянно, то (24)и , (25) и – угловая скорость и угол поворота тела в начальный момент , и – в момент времени . При ускоренном вращении в уравнениях (24) - (25) выбирается знак «+», а при замедленном – знак «-».

6. Закон Ньютона . Инерциальные системы отсчета.

Первый закон Ньютона существуют такие системы отсчета, относительно которых тело сохраняет скорость постоянно или покоится , если на него не действуют другие тела или действие других тел скомпенсировано . Св-во тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах ,действующих на него, называется инертностью.

F_{равнодействующая}=0. F_{равнодейств.} = F₁+F₂+…+F_n

Второй закон Ньютона ускорение тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела : . 2 з-н Ньютона устанавливает взаимосвязь между силой, которая на него действует, массой тела и ускорением ,которое оно приобретает. Этот з-н используется для введения единицы силы в системе СИ. Она называется ньютона(Н). 1Н- сила, под действием которой тело массой 1кг приобретает ускорение 1 м/c² . 1Н = 1 (кг*м) / c² . для того чтобы найти направление ускорении тела ,надо найти направление результирующей силы, действующей на тело .Эти два принципа совпадают .

m*a= F₁+F₂+…+F_n F_{равнодейств.}= m*a

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил.

где  — импульс точки,  — её скорость, а  — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени^. Иногда предпринимаются попытки распространить сферу применения уравнения и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила

Второй закон Ньютона, как и вся классическая механика, действителен только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.

Следует учитывать, что нельзя рассматривать частный случай (при ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Третий закон Ньютона объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F₁₂, а второе — на первое с силой F₂₁. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия, F₂₁ = −F₁₂. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U(|r₁-r₂|). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:

Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.