Механика
Механическое движение. Материальная точка. Система отсчета. Принцип относительности Галилея.
Механическое движение – это изменение положения тела в пространстве относительно других тел. Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляется относительность механического движения. Далее кратко рассмотрим основные виды механического движения. Поступательное движение – это движение тела, при котором все его точки движутся одинаково. Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение. Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось. Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное. Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях. Например, колебательное движение совершает маятник в часах. Поступательное и вращательное движения – самые простые виды механического движения.
Материальная точкаВо многих случаях размером тела можно пренебречь, так как размеры этого тела малы по сравнению с расстоянием, которое походит это тело, или по сравнению с расстоянием между этим телом и другими телами. Такое тело для упрощения расчетов условно можно считать материальной точкой, имеющей массу этого тела. Материальная точка – это тело, размерами которого в данных условиях можно пренебречь. Многократно упоминавшийся нами автомобиль можно принять за материальную точку относительно Земли. Но если человек перемещается внутри этого автомобиля, то пренебрегать размерами автомобиля уже нельзя. Как правило, решая задачи по физике, рассматривают движение тела как движение материальной точки, и оперируют такими понятиями, как скорость материальной точки, ускорение материальной точки, импульс материальной точки, инерция материальной точки и т.п.
Система отсчётаМатериальная точка движется относительно других тел. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчёта. Тело отсчёта выбирают произвольно в зависимости от решаемых задач. С телом отсчёта связывается система координат, которая представляет из себя точку отсчёта (начало координат). Система координат имеет 1, 2 или 3 оси в зависимости от условий движения. Положение точки на линии (1 ось), плоскости (2 оси) или в пространстве (3 оси) определяют соответственно одной, двумя или тремя координатами. Для определения положения тела в пространстве в любой момент времени также необходимо задать начало отсчёта времени. Система отсчёта – это система координат, тело отсчета, с которым связана система координат, и прибор для измерения времени. Относительно системы отсчёта и рассматривается движение тела. У одного и того же тела относительно разных тел отсчёта в разных системах координат могут быть совершенно различные координаты. Траектория движения также зависит от выбора системы отсчёта. Виды систем отсчёта могут быть различными, например, неподвижная система отсчёта, подвижная система отсчёта, инерциальная система отсчёта, неинерциальная система отсчёта.
ГАЛИЛЕЯ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
принцип физ. равноправия всех инерциальных систем отсчёта (и. с. о.) в классич. механике, проявляющегося в том, что законы механики во всех таких системах одинаковы. Отсюда следует, что никакими механич. опытами, проводящимися в какой-либо и. с. о., нельзя определить, покоится данная система или движется равномерно и прямолинейно. Это положение было впервые установлено итал. учёным Г. Галилеем в 1636.
Движение матер. точки относительно: её положение, скорость, вид траектории зависят от того, по отношению к какой и. с. о. (телу отсчёта) это движение рассматривается. В то же время законы классич. механики одинаковы
.
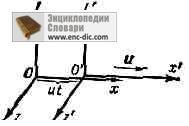
Инерц. система отсчёта L' движется относительно другой инерц. системы отсчёта L в направлении оси х с пост. скоростью u. Координатные оси выбраны так, что в нач. момент времени (t=0) соответствующие оси координат совпадают в обеих системах.
во всех и. с. о. Относительность мехаиич. движения и одинаковость законов механики в разных и. с. о. и составляют содержание Г. п. о. Математически Г. п. о. выражает инвариантность ур-ний механики относительно преобразований координат движущихся точек (и времени) при переходе от одной и. с. о. к другой - преобразования Галилея. Для двух и. с. о.- L и L', движущейся по отношению к L с пост. скоростью и так, как показано на рисунке, преобразования Галилея для координат матер. точки и времени t будут иметь вид:
х'=х-ut, y'=y, z'=z: t'=t (1)
(штрихованные величины относятся к системе L', нештрихованные - к L). Т. о., время в классич. механике, как и расстояние между любыми фиксиров. точками, считается одинаковым во всех системах отсчёта. Из (1) можно получить соотношения между скоростями движения точки и её ускорениями в обеих и. с. о.:
v'=v-и, (2) а'=а.
В классич. механике движение матер. точки (массы т) определяется вторым законом Ньютона:
F=ma, (3)
где F - равнодействующая всех приложенных к ней сил. При этом силы (и массы) явл. инвариантными (не изменяются при переходе от одной системы отсчёта к другой). Поэтому при преобразованиях Галилея ур-ние (3) не меняется. Это и есть матем. выражение Г. п. о.
Г. п. о. справедлив лишь в случае движения тел со скоростями, много меньшими скорости света. При v=c преобразования (1) должны быть заменены преобразованиями Лоренца (см. ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ).