3.Застосування обернених матриць до розв’язування прикладів

Знаходження оберненої матриці є важливою складовою в розділі лінійної алгебри. З допомогою таких матриць, якщо вони існують, можна швидко знайти розв'язок системи лінійних рівнянь. Розглянемо метод Гауса — Йордана, який  використовується для розв'язання систем лінійних алгебраїчних рівнянь, знаходження оберненої матриці, знаходження координат вектора у заданому базисі, відшукання рангу матриці. Метод є модифікацією методу Гауса. Названий на честь Гауса та німецького математика та геодезиста Вільгельма Йордана.

Алгоритм

1. Обирається перша зліва колонка, що містить хоч одне ненульове значення.

2. Якщо верхнє число у цій колонці - нуль, то обмінюється увесь перший рядок матриці з іншим рядком матриці, де у цій колонці нема нуля.

3. Усі елементи першого рядка діляться на верхній елемент обраної колонки.

4. Від рядків, що залишились, віднімається перший рядок, помножений на перший елемент відповідного рядка, з метою отримання у якості першого елемента кожного рядка (крім першого) нуля.

5. Далі, повторюємо ці операції із матрицею, отриманою з початкової матриці після викреслювання першого рядка та першого стовпчика.

6. Після повторення операцій n-1 разів отримаємо верхню трикутну матрицю.

7. Віднімаємо від передостаннього рядка останній рядок, помножений на відповідний коефіцієнт, щоб у передостанньому рядку залишилась лише 1 на головній діагоналі.

8. Повторюємо попередній крок для наступних рядків. У результаті отримуємо одиничну матрицю і рішення на місці вільного вектора (над ним необхідно виконувати ті самі перетворення).

Розгорнутий алгоритм для знаходження оберненої матриці

Нехай дано:

Прямий хід (алгоритм утворення нулів під головною діагоналлю) 

Поділимо перший рядок матриці А на   отримаємо:  , j – стовпець матриці А.

• Повторюємо дії для матриці I , за формулою: 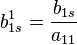 , s – стовпець матриці I

Отримаємо:

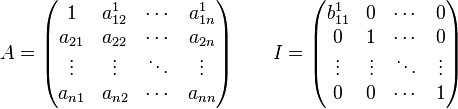
• Будемо утворювати 0 у першому стовбці: .

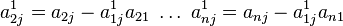
• Повторюємо дії для матриці І, за формулами : 

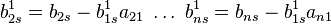
Отримаємо:

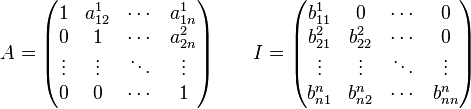
• Продовжуємо виконувати анологічні операції використовуючи формули : 

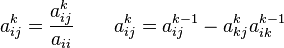
при умові, що 

• Повторюємо дії для матриці І, за формулами : 

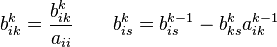
при умові, що  Отримаємо :

Зворотній хід (алгоритм утворення нулів над головною діагоналлю) 

Використаємо формулу:  , при умові, що  Повторюємо дії для матриці І, за формулою  : , при умові, що 

Остаточно отримуємо :

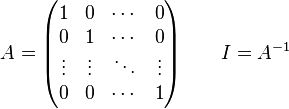
Приклад

Розв'яжемо систему рівнянь:

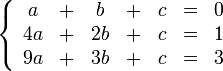
Запишемо її у вигляді матриці 3×4, де останній стовпчик є вільним членом:

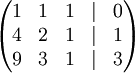
Виконаємо такі дії:

• До рядка 2 додамо: -4 * рядок 1.

• До рядка 3 додамо: -9 * рядок 1.

Отримаємо:

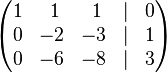
• До рядка 3 додамо: -3 * рядок 2.

• Рядок 2 ділимо на -2

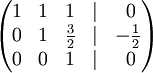
• До рядка 1 додамо: -1 * рядок 3.

• До рядка 2 додамо: -3/2 * рядок 3.

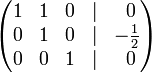
• До рядка 1 додамо: -1 * рядок 2.

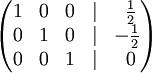
У правому стовпчику отримаємо рішення:

 .

4.Розв’язування прикладів

1. Для матриці A знайти обернену матрицю.

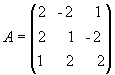
Рішення. Знаходимо спочатку детермінант матриці А:

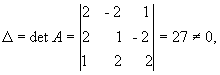
Це означає, що обернена матриця існує і ми її можемо знайти по формулі 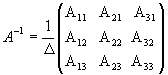, де А_{i j} (i,j=1,2,3) - алгебраїчні доповнення до елементів а_{i j} початкової матриці.

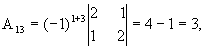
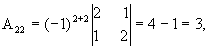
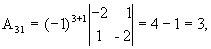
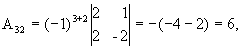
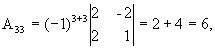
 звідки

.

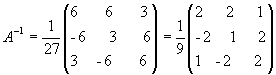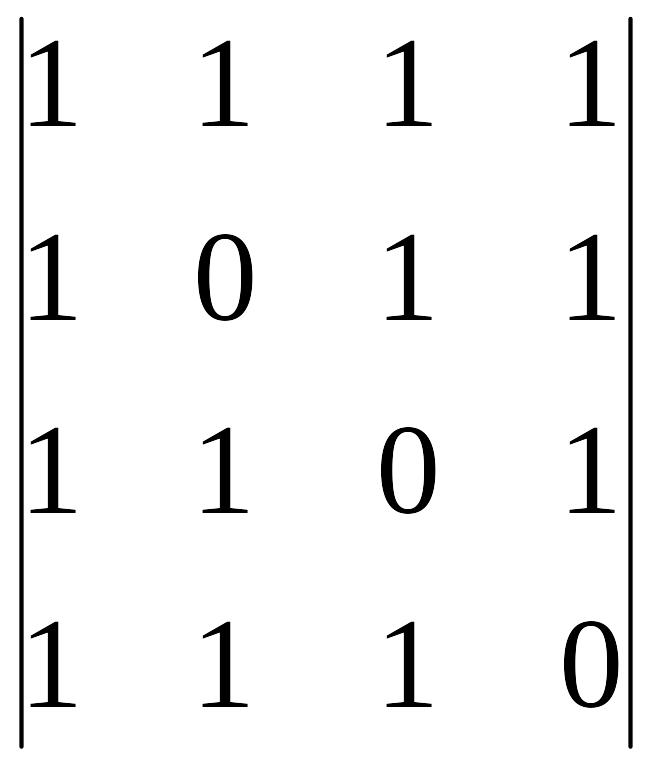
2. Знайти матрицю, обернену до матриці.

A =

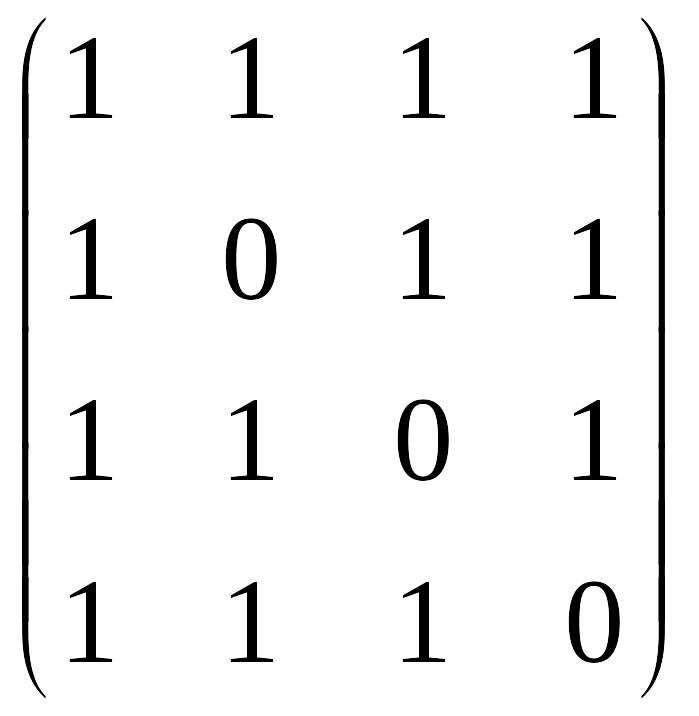
Знаходимо спочатку визначник матриці A:

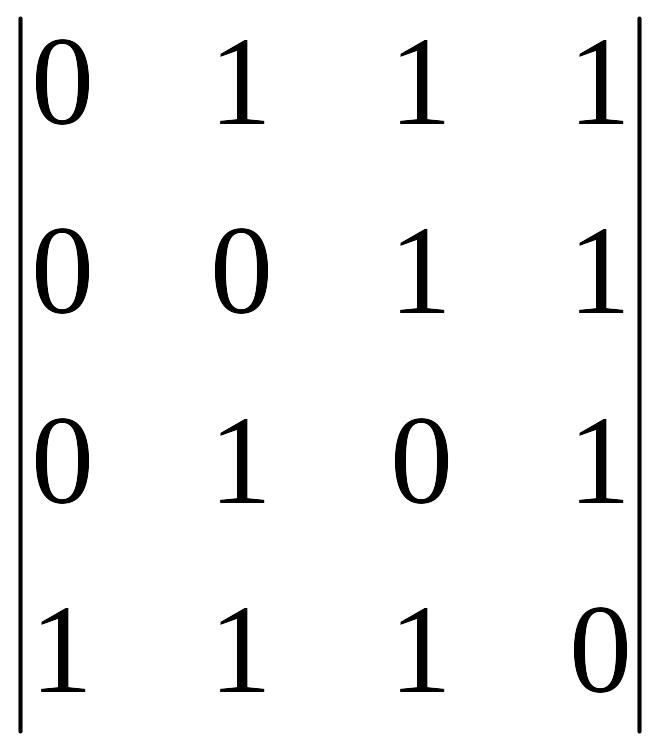= = 1 (-1)⁴⁺¹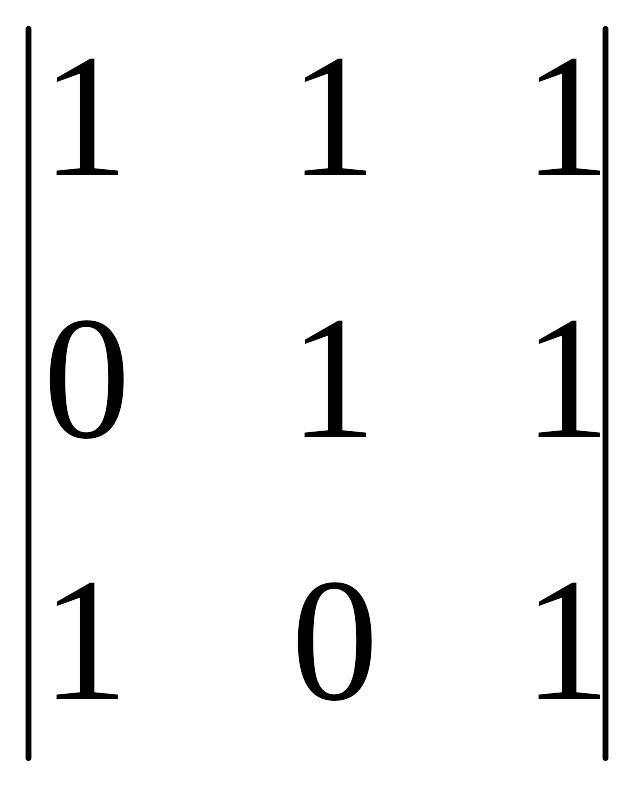 = (-1) =

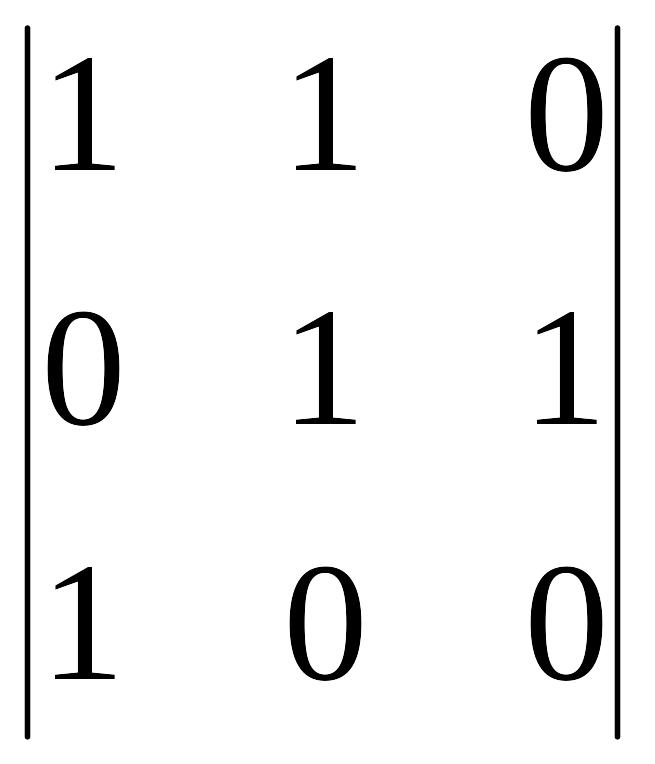= (-1) 1 (-1)³⁺¹ = -1 0. Отже обернена матриця існує.

Знаходимо алгебраїчні доповнення:

A₁₁=(-1)¹⁺¹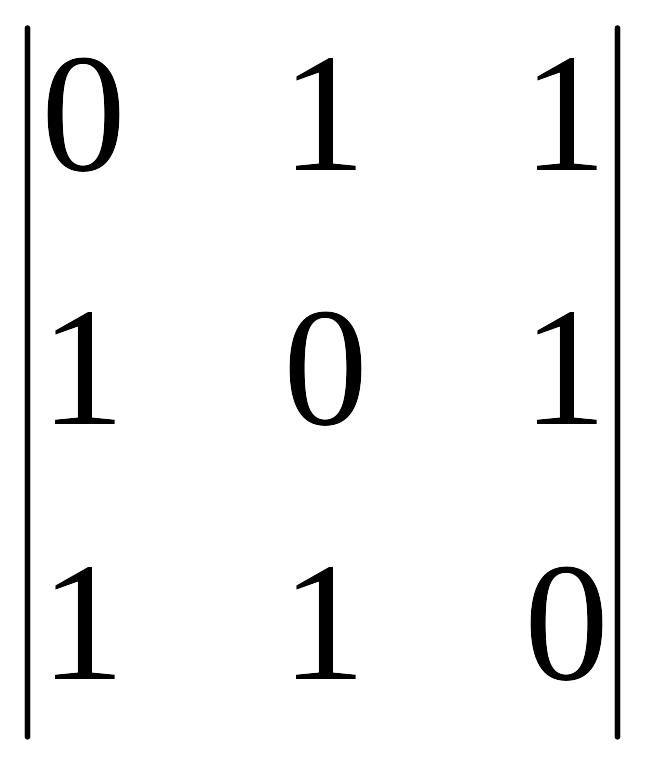 = 2 A₂₁=(-1)²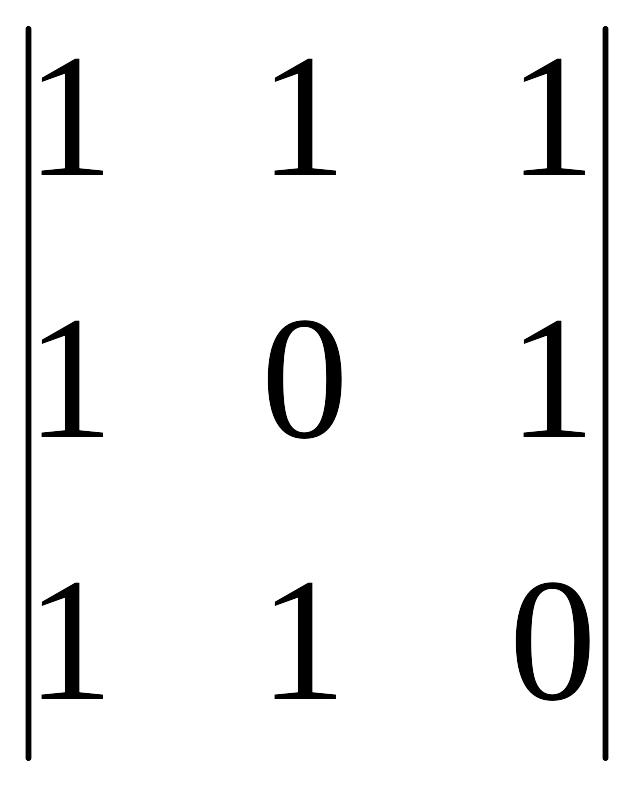⁺¹ = -1

A₃₁=(-1)³⁺¹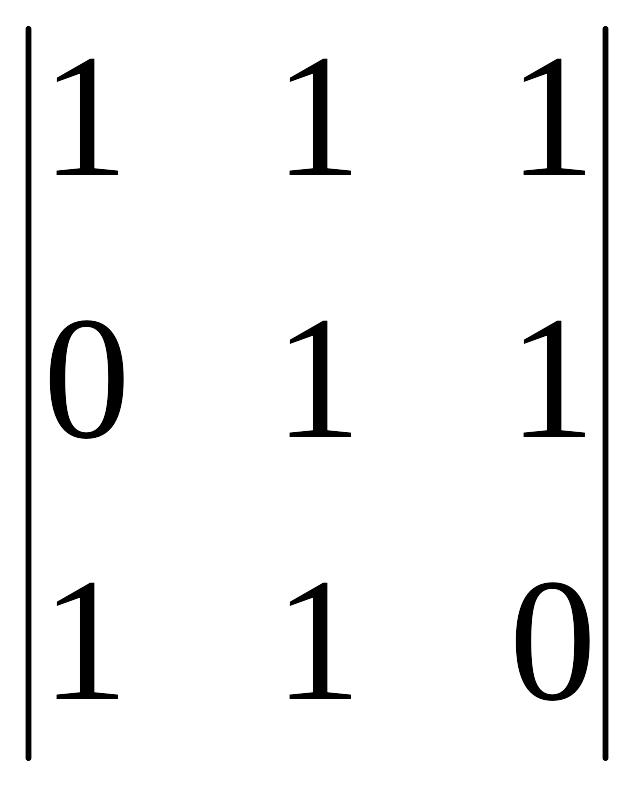 = -1 A₄₁=(-1)⁴⁺¹ = -1

A₁₂=(-1)¹⁺² = -1 A₂₂=(-1)²⁺² = 1

A₃₂=(-1)³⁺²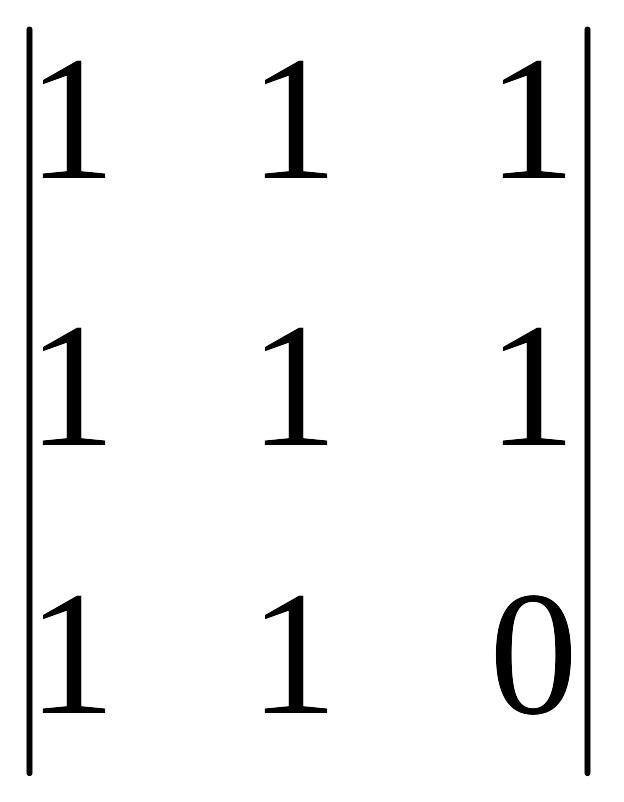 = 0 A₄₂=(-1)⁴⁺² = 0

A₁₃=(-1)¹⁺³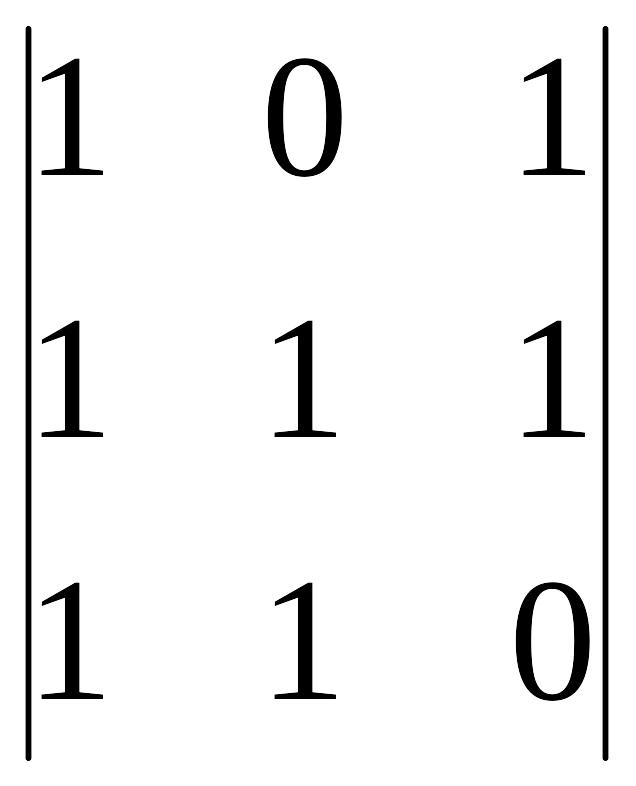 = -1 A₂₃=(-1)²⁺³ = 0

A₃₃=(-1)³⁺³ = 1 A₄₃=(-1)⁴⁺³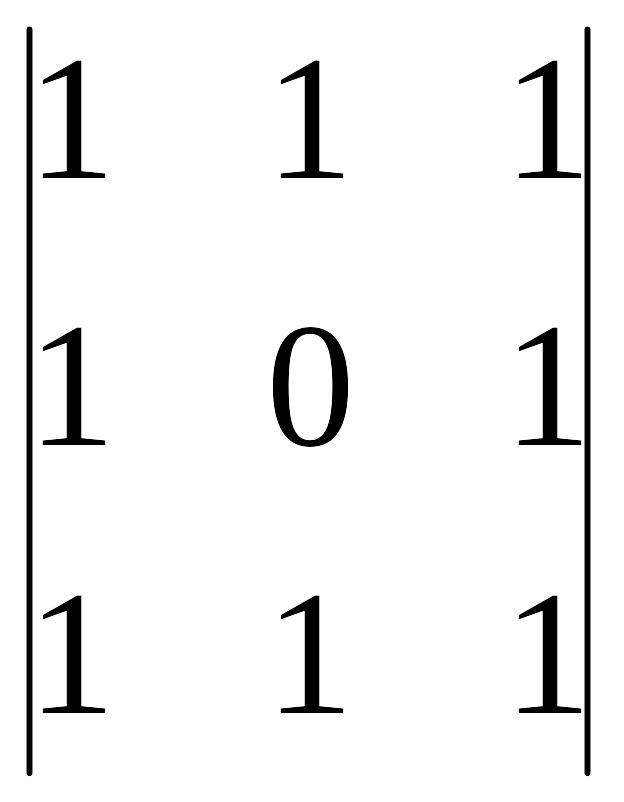 = 0

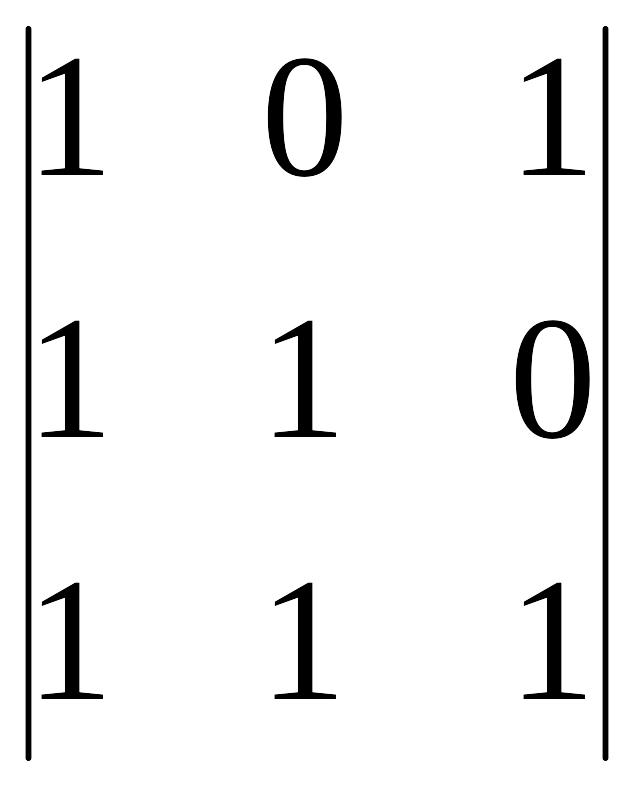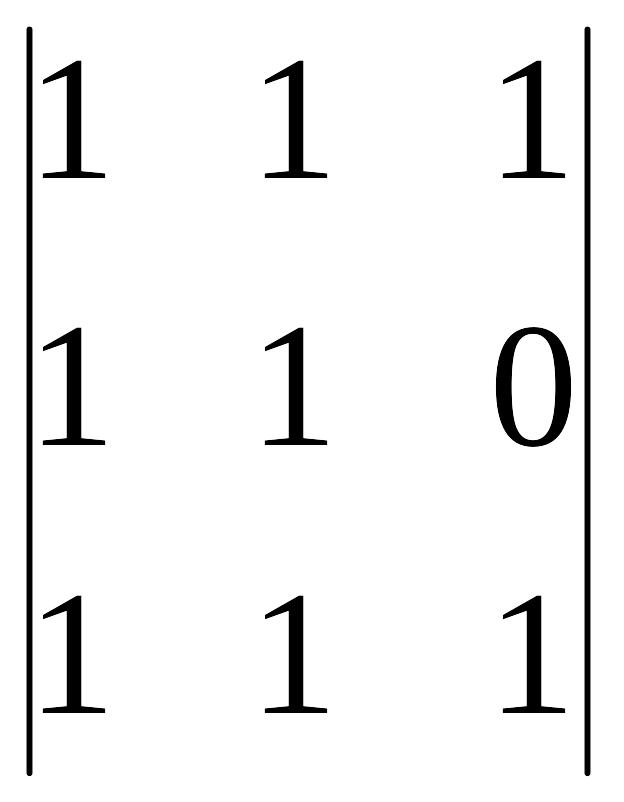A₁₄=(-1)¹⁺⁴ = -1 A₂₄=(-1)²⁺⁴ = 0

A₃₄=(-1)³⁺⁴ = 0 A₄₄=(-1)⁴⁺⁴ = 1

Підставляючи у формулу (3) знайдені значення, одержуємо:

A^-1 =

Перевірка. Одержаний результат можна легко перевірити.

Оскільки, AA^-1 = E, де E –це одинична матриця, то:

A A^-1 = =

=

=

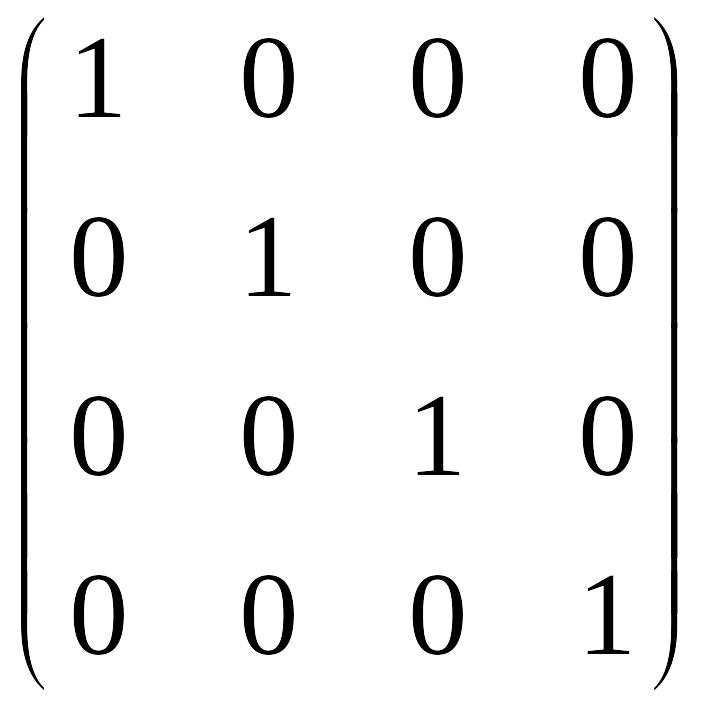
Отже, обернену матрицю знайдено вірно.