2.1.2.Визначення показника заломлення із рівняння дисперсії

Розглянемо альтернативний спосіб визначення n незалежно від порядкових чисел т. Із рівняння (2.3) і (2.4) випливає

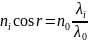(2.16)

У недисперсній області рівняння (2.16) має вигляд

,

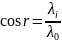і n можна визначити безпосередньо із рівняння (2.7). Рівняння (2.16) можна записати, як:

.

Підстановка рівняння (2.7) у вищезгадане рівняння дає:

(2.17)

а підстановка рівняння (2.2) у рівняння (2.17) дає неоднорідне рівняння в змінних a,bi х. Три таких рівняння можна одержати, якщо розглянути три різні екстремальні величини і a,b,х,можна одержати із цих рівнянь. Щоб дістати правильне значення цих змінних необхідно, щоб довжини хвиль вимірювалися з точністю ̴ 0,1 нм, що нелегко зробити.

Кращим методом являється розклад n_i² у ряд Тейлора навколо n₀ . Із рівняння (2.2) випливає, що:

(2.18)

Підстановка рівняння (2.17) у рівняння (2.18) дає[12]:

(2.19)

де (2.20)

Рівняння (2.2) і (2.19) показують, що N² можна представити як функцію виду:

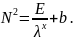(2.21)

Із рівняння (2.17), (2.19), і (2.21) випливає, що:

(2.22)

х можна визначити обчисленням N² для кожної екстремальної величини і повторенням х для того, щоб дістати хорошу відповідність (2.21). Ця регресія також дає значення Е, b. Значення а можна визначити із рівняння (2.22) і трьох постійних у рівнянні (2.2). Таким чином визначається дисперсія показника заломлення.

Щоб дістати т і d із рівняння, аналогічно рівнянню (2.15), можна записати[12]:

(2.23)

На рис.2.2 зображено графік залежності значень від . Екстраполяція прямої лінії через ці точки покаже порядкове число першої екстремальної величини m₁. Пряма лінія через т₁ та інші точки, мають нахил 2d, із якої можна визначити d.

2.2. Експериментальна установка і методика дослідження оптичних констант плівок.

Не дивлячись на те, що вже більше ніж за 50 років із часу відкриття ХСН їх властивості досить добре вивчені, навіть останнім часом не зникає інтерес як до їх технології одержання[13], так і подальше дослідження їх фізико-хімічних, оптичних властивостей та застосування[14-20].

Інтерес до використання різних багатокомпонентних стекол і плівок на їх основі в оптиці підкреслює важливість вивчення оптичних властивостей цих матеріалів. Халькогенідні стекла відрізняються від інших прозорих твердих тіл своїми оптичними константами на діаграмі Аббе і вони мають відносне велике значеня показника заломлення n і низький коефіцієнт дисперсії . Халькогенідні тонкоплівкові шари, що використовуються у наших дослідженнях, відносяться до сімейства системи As-Se.

Для вимірювання коефіцієнту пропускання використовувався спектрофотометр СФ-46. В основу роботи спектрофотометра СФ-46 покладений принцип вимірювання відношення інтенсивностей двох світлових потоків: потоку, що пройшов через досліджуваний зразок, і потоку, падаючого на досліджуваний зразок (або що пройшов через контрольний зразок). Структурна схема спектрофотометра представлена на рис. 2.3.

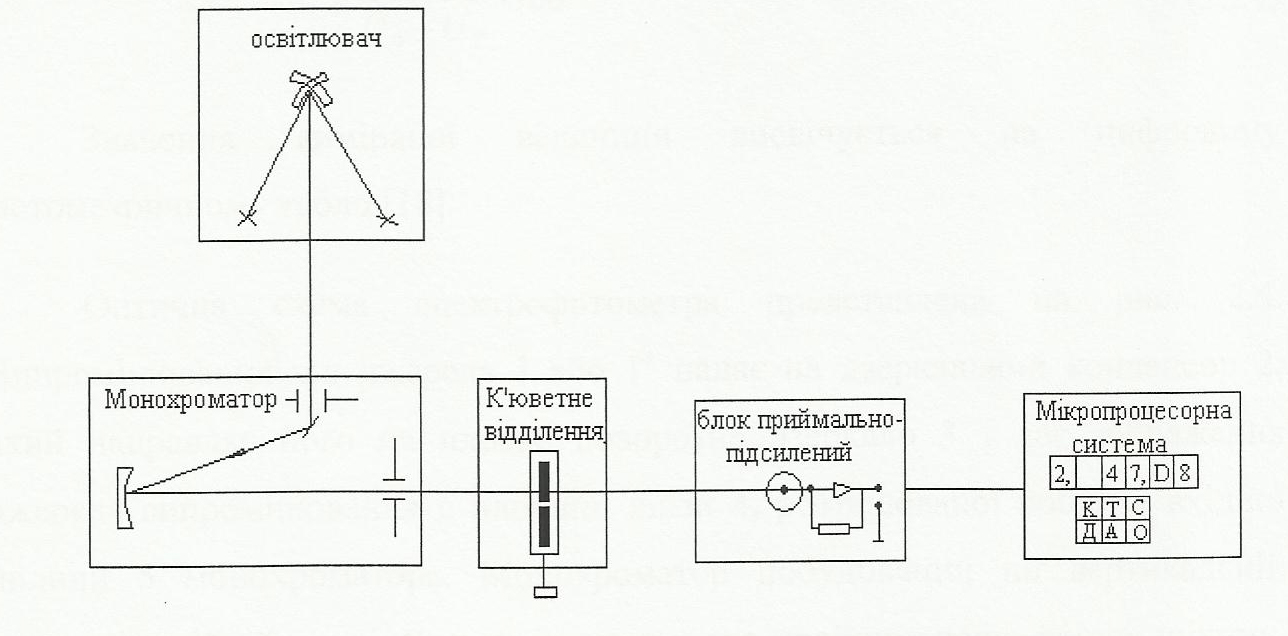
Рис. 2.3. Структурна схема спектрофотометра СФ-46 [21].

Світловий пучок з освітлювача потрапляє в монохроматор через вхідну щілину і розкладається дифракційною граткою в спектр. У монохроматичний потік випромінювання, що поступає з вихідної щілини в кюветне відділення, по черзі вводяться контрольний і досліджуваний зразки. Випромінювання, що пройшло через зразок, потрапляє на катод фотоелемента в приймально-підсилювальному блоці. Електричний струм, що проходить через резистор, який включений в анодний ланцюг фотоелемента, створює на резисторі падіння напруги, пропорційне потоку випромінювання, падаючому на фотокатод.

Підсилювач постійного струму з коефіцієнтом підсилення, близьким до одиниці, забезпечує передачу сигналів на вхід мікропроцесорної системи (далі – МПС). МПС по команді оператора по черзі вимірює і запам’ятовує напруги U_T , U₀ і U, пропорційні темновому струму фотоелемента, потоку, що пройшов через контрольний зразок, і потоку, що пройшов через досліджуваний зразок. Після вимірювання МПС розраховує коефіцієнт пропускання Т досліджуваного зразка по формулі:

(2.24)

Значення виміряної величини висвічується на цифровому фотометричному табло [21].

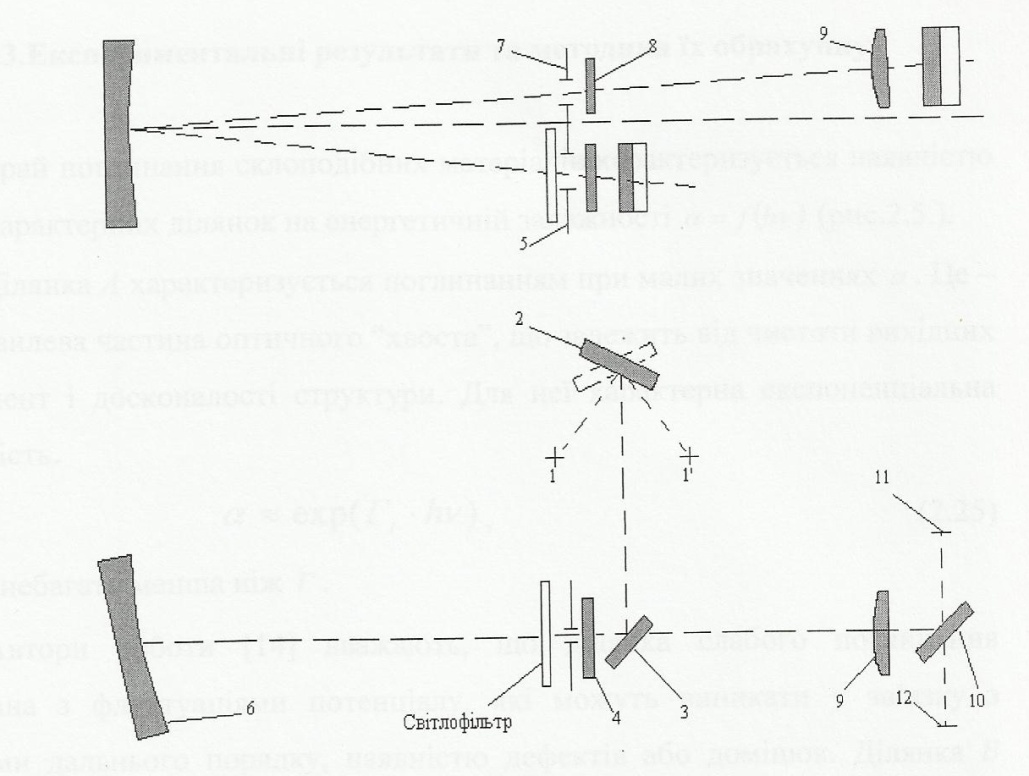
Оптична схема спектрофотометра представлена на рис. 2.4. Випромінювання від джерела 1 або 1' падає на дзеркальний конденсатор 2, який направляє його на плоске поворотне дзеркало 3 і дає зображення джерела випромінювання в площині лінзи 4, розташованої поблизу вхідної щілини 5 монохроматора. Монохроматор побудований по вертикальній автоколімаційній схемі. Випромінювання, що пройшло через вхідну щілину, падає на увігнуту дифракційну гратку 6 із змінним кроком і криволінійним штрихом. Гратки виготовляються на сферичній поверхні, тому, крім диспергуючих властивостей, вона володіє властивістю фокусувати спектр. Застосування змінного кроку і криволінійного штриха значно зменшує абераційні спотворення увігнутих дифракційних граток і дозволяє одержати високу якість спектру у всьому робочому спектральному діапазоні.

Дифрагований пучок фокусується в площині вихідної щілини 7 монохроматора, розташованої над вхідною щілиною 5.

Сканування здійснюється поворотом дифракційної гратки, при цьому монохроматичне випромінювання різних довжин хвиль проходить через вихідну щілину 7, лінзу 8, контрольний або вимірювальний зразок, лінзу 9 з допомогою поворотного дзеркала 10 потрапляє на світлочутливий шар фотоелемента 11 або 12.

7

8

9

5

2

1

1ʹ

11

4

3

6

9

10

12

Світлофільтр

Рис. 2.4. Оптична схема спектрофотометра СФ-46 [21].