
- •§ 21. Пряма лінія в афінній системі координат
- •§ 22. Розміщення прямої відносно системи координат.
- •§ 24. Взаємне розташування двох прямих
- •Теорема 15.
- •§25. Пучки прямих
- •§ 26. Пряма в прямокутній системі координат
- •§ 27. Відстань від точки до прямої
- •§ 28. Кут між прямими
- •§ 29. Рівняння площини в афінній системі координат
- •Теорема 16.
- •Приклад 32.
- •§ 30. Площина в прямокутній системі координат
- •§ 31. Відстань від точки до площини
- •§ 32. Кут між площинами
- •§ 33. Пучок і в’язка площин
- •§ 34. Розміщення площини відносно системи координат
- •§ 36. Взаємне розташування двох площин.
- •§ 37. Взаємне розташування трьох площин.
- •§ 38. Пряма лінія у просторі
- •2. Рівняння прямої за двома точками
- •3. Параметричні рівняння прямої
- •§ 39. Взаємне розташування двох прямих у просторі
- •§ 40. Взаємне розташування прямої і площини
- •§ 41. Метричні задачі на пряму і площину
- •§ 1. Перетворення площини. Група перетворень площини та її підгрупи
- •§ 2. Рухи площини. Властивості рухів
- •§ 3. Два види руху. Аналітичне задання руху
- •§ 4. Класифікація рухів площини
- •§ 5. Група рухів площини і її підгрупи
- •§ 6. Перетворення подібності. Гомотетія як приклад перетворення подібності. Властивості гомотетії
- •§ 7. Аналітичне задання подібності. Властивості подібності
- •§ 8. Класифікація перетворень подібності
- •§ 9. Група подібності та її підгрупи
- •§ 10. Афінні перетворення
- •§ 11. Аналітичне задання афінного перетворення. Група афінних перетворень
- •§ 12. Поняття квадратичної форми
- •§ 13. Зведення квадратичної форми до канонічного вигляду в n-вимірному векторному просторі
- •§ 14. Криві другого порядку та їх класифікація.
- •§ 15. Поверхні другого порядку та їх класифікація.
- •§ 16. Зведення квадратичної форми до канонічного вигляду в евклідовому векторному просторі
- •§ 18. Гіпербола.
- •§ 19. Парабола.
- •§ 20. Афінна еквівалентність еліпсів (гіпербол). Подібність парабол
- •§ 21. Рівняння еліпса, гіперболи і параболи в полярній системі координат
- •§ 22. Дотичні до кривих другого порядку
- •§ 23. Оптичні властивості еліпса, гіперболи та параболи
- •§ 24. Поверхні обертання
- •§ 26. Конус
- •§ 27. Однопорожнинний гіперболоїд
- •§ 28. Двопорожнинний гіперболоїд
- •§ 29. Еліптичний параболоїд
- •§ 30. Гіперболічний параболоїд
- •§ 31. Циліндричні поверхні
- •Приклад 10.
- •§ 32. Прямолінійні твірні поверхонь другого порядку
- •§ 33. Дотична площина до поверхні другого порядку
§ 32. Прямолінійні твірні поверхонь другого порядку
Пряма, яка лежить на поверхні, називається прямолінійною твірною цієї поверхні.
Отже, твірні конуса і циліндричної поверхні являються їх прямолінійними твірними. Є і інші поверхні другого порядку, які можуть утворитися з прямих ліній. Такі властивості мають однопорожнинний гіперболоїд та гіперболічний параболоїд (очевидно, що еліпсоїд, двопорожнинний гіперболоїд і еліптичний параболоїд не мають прямолінійних твірних).
Розглянемо однопорожнинний гіперболоїд: .
Запишемо:
 або
або
 .
.
Складемо систему рівнянь
 , де α довільне дійсне число (31)
, де α довільне дійсне число (31)
При фіксованому значенні α ця система визначає пряму лінію (задану як перетин двох площин). Змінюючи α ми отримаємо сукупність (сім’ю) прямих. Кожна з цих прямих лежить на поверхні однопорожнинного гіперболоїда. Дійсно, якщо координати деякої точки задовольняють систему (31), то, перемноживши рівняння цієї системи, отримаємо рівняння однопорожнинного гіперболоїда. Отже, довільна точка прямої (31) належить однопорожнинному гіперболоїду, тобто ці прямі є прямолінійними твірними.
Аналогічно, можна отримати ще одну систему (сім’ю) прямолінійних твірних однопорожнинного гіперболоїда:
 , де β довільний параметр (32)
, де β довільний параметр (32)
Основні властивості прямолінійних твірних:
Через довільну точку поверхні проходить дві і тільки дві прямолінійні твірні, одна з сімейства (31), а інша з сімейства (32).
Будь-які дві прямолінійні твірні одного сімейства – мимобіжні.
Будь-які дві прямолінійні твірні різних сімейств належать одній площині.
Зауважимо, що, крім розглянутих сімей прямолінійних твірних є ще дві прямолінійні твірні однопорожнинного гіперболоїда, які лежать у площинах, паралельних до площини XOZ. Це такі прямі:
 і
і
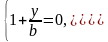
Ці прямі відповідають значенням α= і β=. Вони разом із сімействами (31) і (32) визначають усі прямолінійні твірні однопорожнинного гіперболоїда.
Властивість однопорожнинного гіперболоїда (складатися з прямолінійних твірних) використовується на практиці – побудова башт, радіо і телещогл і ін. Ідея такого використання належить російському інженерові В.Г.Шухову (1853-1939р.), який запропонував конструкцію з металевих балок, розміщених так, як прямолінійні твірні однопорожнинного гіперболоїда обертання. Такі конструкції виявилися дуже міцними і легкими, що й зумовило їх широке використання в будівництві.
Гіперболічний параболоїд має рівняння : .
Записавши це рівняння так:
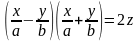 ,
отримаємо дві системи рівнянь, які
визначають дві сім’ї прямолінійних
твірних
,
отримаємо дві системи рівнянь, які
визначають дві сім’ї прямолінійних
твірних
гіперболічного параболоїда:
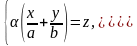 (33) і
(33) і  (34)
(34)
Вони мають такі ж властивості, як і
прямолінійні твірні однопорожнинного
гіперболоїда. Крім того, легко бачити,
що всі твірні з сімейства (33) паралельні
до площини
 ,
а з сімейства (34) паралельні до площини
,
а з сімейства (34) паралельні до площини
 .
.
§ 33. Дотична площина до поверхні другого порядку
Еліпсоїд і гіперболоїди можна задати
рівнянням
 ,
де
– не від’ємні одночасно.
,
де
– не від’ємні одночасно.
Розглянемо пряму
задану параметричними рівняннями:
Знайдемо точки перетину прямої
з поверхнею (підставимо рівняння прямої
в поверхню):
 ,
або
,
або
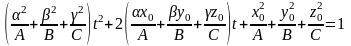 .
.
Якщо отримане квадратне рівняння має
два дійсних кореня
 ,
то це параметри точок перетину прямої
і поверхні. Підставивши їх в рівняння
прямої, отримаємо координати точок
перетину.
,
то це параметри точок перетину прямої
і поверхні. Підставивши їх в рівняння
прямої, отримаємо координати точок
перетину.
Якщо ж розв’язки збігаються
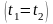 ,
то пряма
–
дотикається до поверхні.
,
то пряма
–
дотикається до поверхні.
Виберемо на поверхні деяку точку
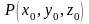 .
Дотична до будь-якої лінії на поверхні,
яка проходить через точку P, називається
дотичною до поверхні в цій точці.
.
Дотична до будь-якої лінії на поверхні,
яка проходить через точку P, називається
дотичною до поверхні в цій точці.
Покажемо, що геометричне місце дотичних до поверхні в заданій точці P являє собою площину.
Так
як точка
належить поверхні, то її координати
задовольняють рівняння поверхні отже,
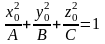 і маємо рівняння:
і маємо рівняння:
 .
.
Оскільки – дотична, то корені цього рівняння рівні .
Так
як
,
то і
,
що можливо лише у випадку, коли
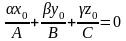 .
.
З
рівнянь прямої знаходимо:
,
,
 і підставивши ці значення в останню
рівність, отримаємо геометричне місце
дотичних до поверхні:
і підставивши ці значення в останню
рівність, отримаємо геометричне місце
дотичних до поверхні:
 .
.
Очевидно, що отримане рівняння є рівнянням площини, яка називається дотичною площиною до поверхні в точці .
Оскільки
точка P
належить поверхні, то
і рівняння площини приймає вигляд
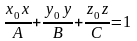 .
.
Отже,
рівняння дотичних площин до еліпсоїда
і гіперболоїдів матимуть вигляд:
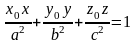 (еліпсоїда),
(еліпсоїда),
 (однопорожнинного
гіперболоїда),
(однопорожнинного
гіперболоїда),
 (двопорожнинного
гіперболоїда).
(двопорожнинного
гіперболоїда).
Аналогічно отримують рівняння дотичних площин до параболоїдів в точці :
 (еліптичного
параболоїда),
(еліптичного
параболоїда),
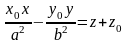 (гіперболічного
параболоїда).
(гіперболічного
параболоїда).
Y
§ 21. Пряма лінія в афінній системі координат 1
§ 22. Розміщення прямої відносно системи координат. 3
§ 23. Геометричний зміст знака Ax+By+C 4
§ 24. Взаємне розташування двох прямих 5
Теорема 15. 6
§25. Пучки прямих 7
§ 26. Пряма в прямокутній системі координат 7
§ 27. Відстань від точки до прямої 9
§ 28. Кут між прямими 11
§ 29. Рівняння площини в афінній системі координат 11
Теорема 16. 13
Приклад 32. 14
Скласти параметричні рівняння площини 6x – 3y + z – 5 = 0. 14
§ 30. Площина в прямокутній системі координат 14
§ 31. Відстань від точки до площини 15
§ 32. Кут між площинами 16
§ 33. Пучок і в’язка площин 16
§ 34. Розміщення площини відносно системи координат 17
§ 35. Геометричний зміст знака Ax+By+Cz+D 18
§ 36. Взаємне розташування двох площин. 19
§ 37. Взаємне розташування трьох площин. 19
§ 38. Пряма лінія у просторі 20
§ 39. Взаємне розташування двох прямих у просторі 23
§ 40. Взаємне розташування прямої і площини 24
§ 41. Метричні задачі на пряму і площину 25
§ 1. Перетворення площини. Група перетворень площини та її підгрупи 29
§ 2. Рухи площини. Властивості рухів 30
§ 3. Два види руху. Аналітичне задання руху 33
§ 4. Класифікація рухів площини 34
§ 5. Група рухів площини і її підгрупи 35
§ 6. Перетворення подібності. 37
Гомотетія як приклад перетворення подібності. Властивості гомотетії 37
§ 7. Аналітичне задання подібності. 39
Властивості подібності 39
§ 8. Класифікація перетворень подібності 41
§ 9. Група подібності та її підгрупи 42
§ 10. Афінні перетворення 42
§ 11. Аналітичне задання афінного перетворення. Група афінних перетворень 44
§ 12. Поняття квадратичної форми 45
§ 13. Зведення квадратичної форми до канонічного вигляду в n-вимірному векторному просторі 46
§ 14. Криві другого порядку та їх класифікація. 49
§ 15. Поверхні другого порядку та їх класифікація. 52
§ 16. Зведення квадратичної форми до канонічного вигляду в евклідовому векторному просторі 54
§ 17. Еліпс 57
§ 18. Гіпербола. 60
§ 19. Парабола. 61
§ 20. Афінна еквівалентність еліпсів (гіпербол). 63
Подібність парабол 63
§ 21. Рівняння еліпса, гіперболи і параболи в полярній системі координат 64
§ 22. Дотичні до кривих другого порядку 66
§ 23. Оптичні властивості еліпса, гіперболи та параболи 68
§ 24. Поверхні обертання 71
§ 25. Еліпсоїд 72
§ 26. Конус 73
§ 27. Однопорожнинний гіперболоїд 74
§ 28. Двопорожнинний гіперболоїд 75
§ 29. Еліптичний параболоїд 76
§ 30. Гіперболічний параболоїд 77
§ 31. Циліндричні поверхні 78
Приклад 10. 80
§ 32. Прямолінійні твірні поверхонь другого порядку 81
Основні властивості прямолінійних твірних: 81
1. Через довільну точку поверхні проходить дві і тільки дві прямолінійні твірні, одна з сімейства (31), а інша з сімейства (32). 81
2. Будь-які дві прямолінійні твірні одного сімейства – мимобіжні. 81
3. Будь-які дві прямолінійні твірні різних сімейств належать одній площині. 81
§ 33. Дотична площина до поверхні другого порядку 82
