§ 24. Поверхні обертання

Поверхня, яка разом з будь-якою своєю точкою містить все коло, отримане обертанням цієї точки навколо деякої фіксованої прямої, називається поверхнею обертання (рис. 18).

Пряма, навколо якої виконується обертання, називається віссю обертання. Якщо поверхню обертання перетинати площинами, перпендикулярними до вісі обертання, то отримаємо кола. Такі кола називаються паралелями поверхні. Площини, які проходять через вісь обертання, перетинають поверхню обертання по лініях, які називаються меридіанами.

Нехай в прямокутній системі координат ( ) задана лінія , яка лежить в площині . Тоді вона має рівняння . Знайдемо рівняння поверхні, яка утвориться при обертанні лінії навколо осі 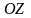. Візьмемо на поверхні довільну точку 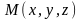і проведемо через неї площину, перпендикулярну до осі . В перетині з поверхнею обертання отримаємо коло з центром в точці , радіуса . З іншого боку, цей радіус є абсцисою точки лінії , апліката якої . Підставивши в рівняння лінії , , отримаємо рівняння поверхні обертання навколо осі : 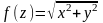, або

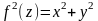(21)

Отже, щоб отримати рівняння поверхні обертання, утвореної обертанням лінії , що лежить в площині , навколо осі , потрібно в рівнянні цієї лінії замінити x на .

Аналогічно можна отримати поверхні обертання навколо інших координатних осей.

§ 25. Еліпсоїд

Еліпсоїдом називається поверхня, яка в деякій прямокутній системі координат визначається рівнянням:

(22)

Величини a, b, c називаються півосями еліпсоїда.

Дослідимо форму еліпсоїда і побудуємо його:

1. Так як x, y, z, входять в рівняння (22) тільки в парних степенях, то еліпсоїд симетричний відносно координатних площин, осей і початку координат. Центр симетрії еліпсоїда називається центром еліпсоїда, а вісі симетрії – його осями.

Точки перетину еліпсоїда з осями координат: А₁(а,0,0); А₂(-а,0,0); В₁(0,b,0); В₂(0,-b,0); С₁(0,0,с); С₂(0,0,-с) називаються вершинами еліпсоїда.

2. Із рівняння (1) маємо: . Аналогічно для y і z: і Отже, всі точки еліпсоїда лежать всередині прямокутного паралелепіпеда із сторонами 2а, 2b, 2с (крім вершин), з центром в точці О.

3. Розглянемо перерізи еліпсоїда координатними площинами і площинами, паралельними до них.

Площина XOY і паралельні до неї площини мають рівняння z=h.

В перетині еліпсоїда з такими площинами отримаємо або .

Можливі три випадки:

1).  h < c, тоді маємо   – еліпс. При зменшенні  h  піввісі його збільшуються і коли h=0, одержуємо еліпс в площині XOY. Побудуємо його (див. рис. 19).

2).  h = c, то одержуємо – дві уявні прямі, що перетинаються в дійсних точках С₁(0,0,с); С₂(0,0,-с).

3).  h > c, то одержуємо рівняння уявного еліпса, отже в цьому випадку площина z=h з еліпсоїдом не має спільних точок.

Повністю аналогічно розглядаються перерізи еліпсоїда площинами x=h і y=h . Побудувавши еліпси в координатних площинах, отримаємо зображення еліпсоїда (рис.19).

Відмітимо, що якщо в рівнянні (22) а,b,с – різні, то еліпсоїд називається трьохвісним, а якщо які-небудь дві із півосей рівні, наприклад а=с, то в перетині з площинами y=h, де  h < b, отримаємо кола (рис.20).

В цьому випадку еліпсоїд можна одержати обертанням еліпса навколо осі OY. Такий еліпсоїд називається еліпсоїдом обертання. Якщо ж в рівнянні (22) а=b=с, то отримаємо сферу радіуса а.