
- •§ 21. Пряма лінія в афінній системі координат
- •§ 22. Розміщення прямої відносно системи координат.
- •§ 24. Взаємне розташування двох прямих
- •Теорема 15.
- •§25. Пучки прямих
- •§ 26. Пряма в прямокутній системі координат
- •§ 27. Відстань від точки до прямої
- •§ 28. Кут між прямими
- •§ 29. Рівняння площини в афінній системі координат
- •Теорема 16.
- •Приклад 32.
- •§ 30. Площина в прямокутній системі координат
- •§ 31. Відстань від точки до площини
- •§ 32. Кут між площинами
- •§ 33. Пучок і в’язка площин
- •§ 34. Розміщення площини відносно системи координат
- •§ 36. Взаємне розташування двох площин.
- •§ 37. Взаємне розташування трьох площин.
- •§ 38. Пряма лінія у просторі
- •2. Рівняння прямої за двома точками
- •3. Параметричні рівняння прямої
- •§ 39. Взаємне розташування двох прямих у просторі
- •§ 40. Взаємне розташування прямої і площини
- •§ 41. Метричні задачі на пряму і площину
- •§ 1. Перетворення площини. Група перетворень площини та її підгрупи
- •§ 2. Рухи площини. Властивості рухів
- •§ 3. Два види руху. Аналітичне задання руху
- •§ 4. Класифікація рухів площини
- •§ 5. Група рухів площини і її підгрупи
- •§ 6. Перетворення подібності. Гомотетія як приклад перетворення подібності. Властивості гомотетії
- •§ 7. Аналітичне задання подібності. Властивості подібності
- •§ 8. Класифікація перетворень подібності
- •§ 9. Група подібності та її підгрупи
- •§ 10. Афінні перетворення
- •§ 11. Аналітичне задання афінного перетворення. Група афінних перетворень
- •§ 12. Поняття квадратичної форми
- •§ 13. Зведення квадратичної форми до канонічного вигляду в n-вимірному векторному просторі
- •§ 14. Криві другого порядку та їх класифікація.
- •§ 15. Поверхні другого порядку та їх класифікація.
- •§ 16. Зведення квадратичної форми до канонічного вигляду в евклідовому векторному просторі
- •§ 18. Гіпербола.
- •§ 19. Парабола.
- •§ 20. Афінна еквівалентність еліпсів (гіпербол). Подібність парабол
- •§ 21. Рівняння еліпса, гіперболи і параболи в полярній системі координат
- •§ 22. Дотичні до кривих другого порядку
- •§ 23. Оптичні властивості еліпса, гіперболи та параболи
- •§ 24. Поверхні обертання
- •§ 26. Конус
- •§ 27. Однопорожнинний гіперболоїд
- •§ 28. Двопорожнинний гіперболоїд
- •§ 29. Еліптичний параболоїд
- •§ 30. Гіперболічний параболоїд
- •§ 31. Циліндричні поверхні
- •Приклад 10.
- •§ 32. Прямолінійні твірні поверхонь другого порядку
- •§ 33. Дотична площина до поверхні другого порядку
§ 2. Рухи площини. Властивості рухів
Перетворення площини зберігає відстані,
якщо відстань між будь-якими двома
точками А і В площини рівна
відстані між їхніми образами А
і В, тобто
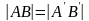 .
.
Перетворення площини, яке зберігає відстані, називається рухом.
Найбільш простим прикладом руху є тотожне перетворення площини, тобто перетворення, при якому кожна точка площини переходить в себе.
Приведемо ще один приклад руху.
Р озглянемо
на площині
озглянемо
на площині
 вектор
.
Кожній точці М площини
поставимо у відповідність точку М
так, щоб
вектор
.
Кожній точці М площини
поставимо у відповідність точку М
так, щоб
 =
.
Ми отримаємо деяке відображення ƒ:
,
яке є перетворенням площини
.
Воно називається паралельним перенесенням
на вектор
.
Якщо
=
,
то паралельне перенесення – тотожне
перетворення.
=
.
Ми отримаємо деяке відображення ƒ:
,
яке є перетворенням площини
.
Воно називається паралельним перенесенням
на вектор
.
Якщо
=
,
то паралельне перенесення – тотожне
перетворення.
Доведемо, що паралельне перенесення є рухом.
Нехай М1 і М2-
дві точки площини (рис. 1), а М1
і М2
– їх образи. Потрібно показати, що
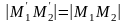 .
.
За означенням паралельного перенесення:
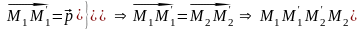 – паралелограм, тому
– паралелограм, тому
 .
.
Отже, паралельне перенесення – рух площини.
Впорядковану трійку точок A, B, C площини, які не лежать на одній прямій називають репером.
Позначають:

Точку A називають початком, а B і C – вершинами.
Я кщо
кщо
 –
довільний, то репер називається афінним
(рис.2).
–
довільний, то репер називається афінним
(рис.2).
Якщо
 ,
і
,
і
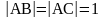 ,
то репер називають ортонормованим.
,
то репер називають ортонормованим.
Фактично репер – це система координат, де А – початок, а В і С кінці базисних векторів.
Очевидно, що при рухові репер переходить
в репер, причому ортонормований репер
переходить в ортонормований репер (так
як
 переходить у рівний йому трикутник
переходить у рівний йому трикутник
 ).
).
Теорема 2. Нехай
 два довільні ортонормовані репери
площини. Тоді існує єдиний рух, який
переводить
два довільні ортонормовані репери
площини. Тоді існує єдиний рух, який
переводить
 ,
причому будь-яка точка М з даними
координатами в репері
,
причому будь-яка точка М з даними
координатами в репері
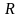 переходить в точку
переходить в точку
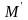 з такими ж координатами в репері
з такими ж координатами в репері
 .
.
Доведення.
Доведемо спочатку, що такий рух існує.
Задамо відображення
 так щоб будь-якій точці М в репері
R відповідала точка
з такими ж координатами в репері
:
так щоб будь-якій точці М в репері
R відповідала точка
з такими ж координатами в репері
:
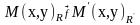 .
.
При цьому відображенні маємо:
 ,
,
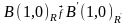 ,
,
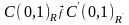 .
.
Таке відображення
 буде взаємно-однозначним, тобто є
перетворенням площини.
буде взаємно-однозначним, тобто є
перетворенням площини.
Покажемо, що
зберігає відстані між точками, тобто є
рухом. Розглянемо точки
 і
і
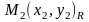 .
Тоді
.
Тоді
 ,
,
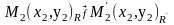 ,
,
 і
і
 .
Отже,
,
тобто
є рухом.
.
Отже,
,
тобто
є рухом.
Покажемо, що
єдиний рух площини, який переводить
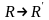 і зберігає координати точок.
і зберігає координати точок.
Припустимо, що існує ще один рух
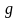 такий, що задовольняє умову теореми.
Але тоді на площині існує така точка М,
що її образ
такий, що задовольняє умову теореми.
Але тоді на площині існує така точка М,
що її образ
 при рухові f не співпадає з її
образом
при рухові f не співпадає з її
образом
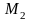 при рухові g.
при рухові g.
Так як
 ,
і
,
і
 ,
то
,
то
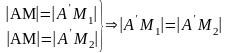 ,
тобто точка
,
тобто точка
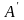 рівновіддалена від точок
і
.
рівновіддалена від точок
і
.
Аналогічно
 ,
,
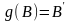 і
і
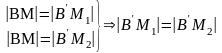 ,
отже точка
,
отже точка
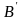 рівновіддалена від точок
і
і
рівновіддалена від точок
і
і
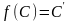 ,
,
 ,
то
,
то
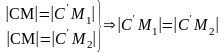 ,
отже, точка
,
отже, точка
 рівновіддалена від точок
і
.
рівновіддалена від точок
і
.
Таким чином точки
,
і
належать серединному перпендикуляру
відрізка
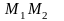 ,
отже, вони лежать на одній прямій, чого
бути не може, так як (
,
,
)
– репер. Отже, припущення не вірне і
існує єдиний рух f, який задовольняє
умову теореми.
,
отже, вони лежать на одній прямій, чого
бути не може, так як (
,
,
)
– репер. Отже, припущення не вірне і
існує єдиний рух f, який задовольняє
умову теореми.
Зупинимося на властивостях руху.
Рух переводить пряму у пряму, причому паралельні прямі в паралельні прямі.
Доведення.
Розглянемо ортонормований репер
 і його образ після руху
і його образ після руху
 .
Нехай пряма l в репері R має
рівняння
.
Нехай пряма l в репері R має
рівняння
 .
Тоді, згідно теореми 2, образ
.
Тоді, згідно теореми 2, образ
 цієї прямої в репері
визначається таким же рівнянням (як
множина образів всіх точок прямої l)
отже, є прямою.
цієї прямої в репері
визначається таким же рівнянням (як
множина образів всіх точок прямої l)
отже, є прямою.
О чевидно,
що пряма
чевидно,
що пряма
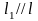 в репері R має рівняння
в репері R має рівняння
 .
При рухові вона перейде в пряму
.
При рухові вона перейде в пряму
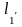 з
таким же рівнянням в репері
отже,
з
таким же рівнянням в репері
отже,
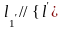 .
.
Рух зберігає просте відношення трьох точок.
Доведення.
Нагадаємо, що простим відношенням
трьох точок, які лежать на одній прямій
 (рис.3) називають таке число
(рис.3) називають таке число
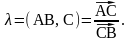
Нехай в репері R три довільні точки
А, В, С прямої мають координати:
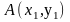 ,
,
 ,
,
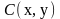 .
.
Тоді координати точки С обчислюються за формулами :
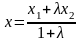 ,
,
 .
.
Нехай репер
– образ репера
при русі. Тоді точки
,
і
мають такі ж координати як і точки А,
В, С, а отже вони пов’язані такими ж
формулами, тобто точка
ділить відрізок
в тому ж відношенні
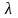 .
.
Як наслідок, середина відрізка переходить в середину відрізка.
З попереднього легко отримати:
3. Рух зберігає поняття „лежати між”.
4.Рух переводить півплощину з границею l в півплощину з границею , де – образ прямої l.
5. Рух переводить промінь в промінь.
6. Рух переводить кут в рівний йому кут (так як переводить трикутник в рівний йому трикутник).
Отже, перпендикулярні прямі при русі переходять в перпендикулярні прямі.
