§ 40. Взаємне розташування прямої і площини

Нехай маємо площину α: Ax+By+Cz+D=0 і пряму l, яка визначається точкою М₀(x₀,y₀,z₀) і направляючим вектором =(α,β,γ). Можна виділити три випадки взаємного розташування прямої і площини:

1. Пряма належить площині.

Розглянемо нормальний вектор площини =(А,В,С) і направляючий вектор =(α,β,γ). Очевидно, що  , отже, їх скалярний добуток · = 0. Крім того, довільна точка прямої повинна належати площині, тому координати точки М₀ повинні задовольняти рівняння площини: Ax₀+By₀+Cz₀+D=0.

2. Пряма паралельна до площини.

· = 0 і Ax₀+By₀+Cz₀+D0.

3. Пряма перетинає площину.

·  0.

Для того, щоб знайти точку перетину прямої і площини, необхідно скласти параметричні рівняння прямої і розв’язати систему:

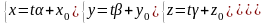. Отримаємо параметр точки перетину. Підставивши його в рівняння прямої, знайдемо координати точки перетину.

Приклад 48.

З’ясувати взаємне розташування прямої: 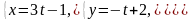і площини .

Розв’язання: Направляючий вектор прямої 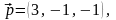а нормальний вектор площини

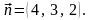
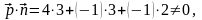отже, пряма перетинає площину.

Для знаходження точки перетину розв'яжемо систему чотирьох заданих рівнянь. Фактично підставимо в рівняння площини замість 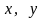і 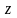їх вирази через параметр :

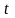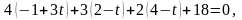звідки Підставивши це значення параметра в рівняння прямої, отримаємо координати точки перетину:

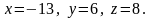
Приклад 49.

Знайти точку, симетричну точці 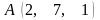відносно площини

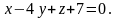
Розв’язання: Знайдемо спочатку ортогональну проекцію точки A на дану площину. Для цього запишемо параметричні рівняння прямої, яка проходить через точку A перпендикулярно до площини. Тоді за направляючий вектор прямої можна взяти нормальний вектор площини Отримаємо рівняння:

Проекцією точки A на площину буде точка перетину отриманої прямої і даної площини. Знайдемо її параметр, підставивши параметричні рівняння в рівняння площини:

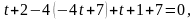звідси 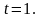Отже, проекція точки A на дану площину має координати (Отримаємо підставивши 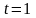в рівняння прямої). Для знаходження симетричної точки скористаємося формулами ділення відрізка навпіл: . Звідси Відповідь:

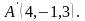
Приклад 50. Знайти ортогональну проекцію точки на пряму

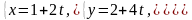
Розв’язання: Ортогональною проекцією точки М на пряму буде точка Р, яку отримаємо в перетині даної прямої з площиною, що проходить через точку 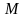перпендикулярно до заданої прямої. Рівняння такої площини знайдемо за точкою і нормальним вектором (направляючий вектор прямої буде нормальним для площини): 2(x–4)+4(y–3)+5(z–10)=0 або 2x+4y+5z–70=0.

Знайдемо параметр точки перетину:

2(1+2t)+4(2+4t)+5(3+5t)–70=0, отже, t=1. Тоді x=3, y=6, z=8.

Відповідь: Р(3, 6, 8).

§ 41. Метричні задачі на пряму і площину

Метричні задачі розглядаються в прямокутній системі координат.

1. Знаходження кута між двома прямими у просторі.

Кутом між прямими називається мінімальний кут між їх направляючими векторами.

Нехай прямі мають направляючі вектори ₁ = (α₁,β₁,γ₁), і ₂= (α₂,β₂,γ₂). Тоді із означення скалярного добутку знаходимо косинус кута між ними:

(46).

Сам кут знайдемо як арккосинус отриманого числа (враховуючи, що кут гострий).

Звідси одразу випливає умова перпендикулярності двох прямих: ₁ ₂ = 0.

Приклад 51.

Знайти кут між прямими: і

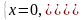
Розв’язання: Знайдемо направляючі вектори даних прямих:

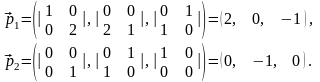
₁ ₂=0, отже,

2. Кут між прямою і площиною

Кутом між прямою і площиною називається гострий кут між прямою і її проекцією на площину.

П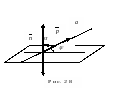 означимо цей кут –  (рис.28). Нехай пряма а має направляючий вектор =(α, β, γ), а площина задана рівнянням Ax+By+Cz+D=0. Тоді кут  між нормальним вектором площини =(А,В,С) і направляючим вектором прямої дорівнює 90⁰– ; або 90⁰+, якщо нормальний вектор направлений вниз (рис.28).

Косинус кута між векторами знаходимо із скалярного добутку: 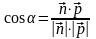. Враховуючи, що сos(90⁰– φ) = sinφ, сos(90⁰+) = – sinφ, маємо sin = |cos|. Отже, ми отримали формулу для знаходження синуса кута між прямою і площиною:

(47)

Приклад 52.

Знайти кут між прямою: 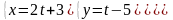і площиною

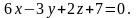
Розв’язання: .

Отже,

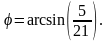
3. Відстань від точки до прямої у просторі:

Н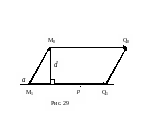 ехай пряма а задана точкою М₁(x₁,y₁,z₁) і направляючим вектором =(α, β, γ). Потрібно знайти відстань d від точки М₀(x₀,y₀,z₀) до даної прямої а (рис.29).

Відкладемо вектор від точки М₁. Отримаємо вектор = .

Розглянемо паралелограм М₁М₀Q₀Q₁. Ясно, що відстань d від точки М₀ до даної прямої а дорівнює висоті паралелограма М₁М₀Q₀Q₁, яку обчислимо, розділивши площу паралелограма на довжину сторони М₁Q₁, тобто на модуль вектора . Площу паралелограма знайдемо як модуль векторного добутку векторів, які утворюють цей паралелограм:

S=d | |=|[ ,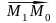 ]|. Знайдемо координати вектора =(x₀-x₁,y₀-y₁,z₀-z₁).

Тоді .

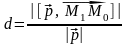Перейшовши до координат, отримаємо:

d = (48)

Відмітимо, що відстань d можна знайти і як відстань між двома точками: точкою М₀ і її ортогональною проекцією на дану пряму (див. приклад 50).

Приклад 53.

Знайти відстань між паралельними прямими і

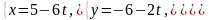
Розв’язання: Відстань між паралельними прямими можна знайти, як відстань від будь-якої точки однієї прямої до іншої прямої. Наприклад, прямій, заданій параметричними рівняннями, належить точка Знайдемо відстань від неї до першої прямої; яка проходить через точку і має направляючим вектор Знайдемо координати вектора 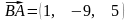і скористаємось формулою (48):

Відповідь:

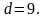
4. Відстань між мимобіжними прямими.

Р озглянемо мимобіжні прямі а₁, яка проходить через точку М₁(x₁,y₁,z₁), і має направляючий вектор ₁ =(α₁,β₁,γ₁), та а₂, яка проходить через точку М₂(x₂,y₂,z₂) і має направляючий вектор ₂=(α₂,β₂,γ₂) (рис.30). Відкладемо вектор ₂ від точки М_1, тоді вектор = ₂. Розглянемо паралелепіпед, побудований на векторах _{1 , 2}, і . Згідно теореми 12, об’єм цього паралелепіпеда рівний модулю змішаного добутку векторів _{1 , 2}, та : V=|( ₁, ₂, )|. З іншого боку, об’єм паралелепіпеда можна знайти як добуток площі основи на висоту. (площу основи знаходимо як модуль векторного добутку векторів, які утворюють паралелограм М₁Q₁P₁N₁, тобто векторів ₁  і ₂):

Отже, V=S d=|[ ₁, ₂]|d= |( ₁, ₂, )|.

Звідки d=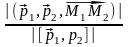 (49)

Приклад 54.

Знайти відстань між мимобіжними прямими: і

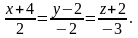
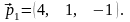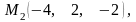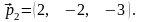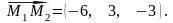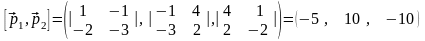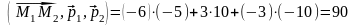
Розв’язання: Перша пряма проходить через точку і має направляючий вектор Друга проходить через точку паралельно до вектора Знайдемо вектор і векторний добуток . Змішаний добуток раціонально обчислити, як скалярний добуток вектора на векторний добуток векторів ₁ і ₂: Отже,

Відмітимо, що відстань між мимобіжними прямими можна знайти й іншим способом, наприклад, як відстань від будь-якої точки однієї прямої до площини, яка проходить через другу пряму, паралельно до першої. Рівняння такої площини отримаємо за двома направляючими векторами і точкою (направляючими векторами площини будуть направляючі вектори даних прямих).