2. Рівняння прямої за двома точками

Нехай пряма проходить через точки М₁(x₁,y₁,z₁) і М₂(x₂,y₂,z₂). Тоді вектор = – є направляючим вектором прямої. Скориставшись рівнянням (42) отримаємо:

. (43)

3. Параметричні рівняння прямої

Нехай пряма задана точкою М₀ (x₀,y₀,z₀) і направляючим вектором =(α,β,γ). Виберемо ще одну довільну точку прямої М (x,y,z) і розглянемо вектор =(x–x₀,y–y₀,z–z₀). || , тому за теоремою 1 =t . Перейшовши до координат, отримаємо:

x–x₀  = α t ; y–y₀ = β t; z–z₀ = γ t, або:

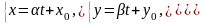(44)

Приклад 43.

Скласти параметричні рівняння прямої, яка проходить через точку A(2,3,-4) паралельно до вісі OY.

Розв’язання:

За направляючий вектор прямої візьмемо вектор 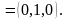Тоді рівняння шуканої прямої матимуть вигляд:

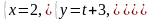
4. Рівняння прямої, заданої як перетин двох площин.

Розглянемо дві площини, задані рівняннями

α: A₁x+B₁y+C₁z+D₁=0 і β: A₂x+B₂y+C₂z+D₂=0, причому їх нормальні вектори неколінеарні (умова перетину), отже, коефіцієнти біля змінних в рівняннях площин не пропорційні. Перетин таких площин визначатиме пряму, яку можна задати системою:

, (45)

причому = (   ) є направляючим вектором прямої.

Приклад 44.

Записати пряму 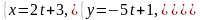як перетин двох площин.

Розв’язання: Спочатку запишемо канонічні рівняння даної прямої: 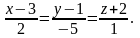. Тепер легко отримати рівняння трьох площин, які проходять через дану пряму. Нам досить записати дві, перетин яких і визначає пряму:

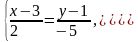
або

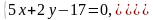
Приклад 45.

Скласти параметричні рівняння прямої, яка проходить через початок координат, паралельно до прямої

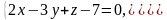
Розв’язання: Знайдемо направляючий вектор даної прямої:

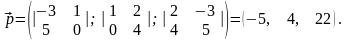Шукана пряма визначається рівняннями:

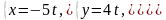
Приклад 46.

Знайти проекцію прямої 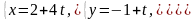на площину

Розв’язання: Проекцією прямої на площину буде пряма, отримана в перетині проектуючої площини з площиною яка має рівняння: Отже, для розв’язання задачі потрібно знайти рівняння проектуючої площини (вона проходить через дану пряму, перпендикулярно до площини 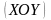). Скористаємося рівнянням площини за точкою і двома направляючими векторами. 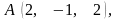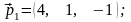За точку можна взяти, явно задану точку прямої а за направляючі вектори – направляючий вектор прямої і нормальний вектор площини:  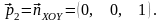   тоді проектуюча площина має рівняння:

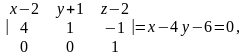
а шукана пряма:

§ 39. Взаємне розташування двох прямих у просторі

Нехай задано прямі l₁ і l₂, які визначаються відповідно: l₁ точкою M₁ і направляючим вектором ₁, а l₂ точкою M₂ і направляючим вектором ₂.

Прямі у просторі можуть бути розташовані таким чином:

1. Співпадають: Тоді ₁ || ₂ || (Колінеарність векторів перевіряємо за теоремою 7, яка стверджує, що у колінеарних векторів координати пропорційні).

2. Паралельні: ₁ || ₂, але не колінеарні з

3. Перетинаються: ₁  не колінеарний з ₂, і вектори ₁ , ₂ і компланарні. Тоді змішаний добуток векторів

( ₁, ₂, )=0).

4. Мимобіжні: Вектори ₁ , ₂ і некомпланарні (змішаний добуток ( ₁, ₂, ) не дорівнює нулю).

Приклад 47.

Дослідити взаємне розташування двох прямих

і

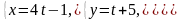
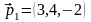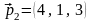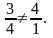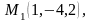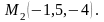
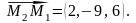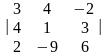
Розв’язання: Направляючі вектори прямих і не колінеарні, так як Отже, прямі перетинаються або мимобіжні. Першій прямій належить точка а другій Змішаний добуток 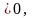тому прямі мимобіжні.