Булева алгебра
Чтобы описать схемы, получаемые сочетанием различных вентилей, нужен особый тип алгебры, в которой все переменные и функции могут принимать только два значения: 0 и 1. Такая алгебра называется булевой (названа в честь английского математика Джорджа Буля 1815-1864).
В булевой
алгебре есть свои функции. Булева функция
на входе получает одну или несколько
переменных и выдает результат, который
зависит только от значений этих
переменных. Можно определить простую
функцию f,
сказав, что
f(A)
= 1, если А = 0, и
f(А) = 0, если А = 1.
Такая функция будет функцией НЕ. Так
как булева функция от п переменных имеет
только
возможных комбинаций значений переменных,
то такую функцию можно полностью описать
в таблице с
строками. В каждой строке будет даваться
значение функции для разных комбинаций
значений переменных. Такая таблица
называется таблицей истинности.
Строки таблицы истинности располагаются по порядку номеров, то есть для двух переменных в порядке 00, 01, 10, 11. Булеву функцию можно полностью описать -разрядным двоичным числом, которое получается, если считывать по вертикали колонку результатов в таблице истинности. Таким образом, НЕ-И - это 1110, НЕ-ИЛИ - 1000, И - 0001 и ИЛИ - 0111.
Существуют только 16 булевых функций от двух переменных, которым соответствуют 16 возможных 4-разрядных цепочек.
На рисунке показана таблица истинности для булевой функции от трех переменных: М = f(A, B,C). Это функция большинства, которая принимает значение 0, если большинство переменных равны 0, или 1, если большинство переменных равны 1.
Рисунок – Схема реализации функции большинства
Таблица истинности для функции большинства
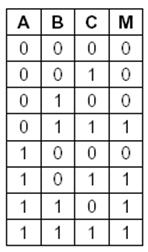
С возрастанием количества переменных описание булевой функции с помощью таблицы истинности становится громоздким. Поэтому вместо таблиц истинности часто используется другой вариант записи.
Любую булеву функцию можно определить, указав, какие комбинации значений входных переменных приводят к единичному значению функции. Для функции большинства существует 4 комбинации переменных, которые дают единичное значение функции. Для того, чтобы показать что значение переменной инвертируется, над переменной ставят черту. Отсутствие черты означает, что значение переменной не инвертируется.
Для обозначения булевой функции И используется знак умножения (точка, ·).
Для обозначения
булевой функции ИЛИ используется знак
сложения (+).
Например,
принимает значение 1, только если
A
= 1, B
= 0 и С = 1. Кроме того,
принимает значение 1, только если (А = 1
и В = 0) или (В = 1 и С = 0). В таблице истинности
функция принимает значение 1 в четырех
строках:
.
Функция М принимает значение истины
(то есть 1), если одно из этих четырех
условий истинно. Следовательно:
.
Это компактная запись таблицы истинности. Таким образом, функцию от n переменных можно описать суммой максимум произведений, при этом в каждом произведении будет по n множителей. Булева функция может быть реализована электронной схемой (часто различными способами) с использованием сигналов, которые представляют входные и выходные переменные, и вентилей, например, И, ИЛИ и НЕ.