Показательное распределение случайной величины: параметры, характерные особенности, функции распределения и плотности вероятности, их графики.

Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Определение

Случайная величина имеет экспоненциальное распределение с параметром , если её плотность имеет вид

.

Пример. Пусть есть магазин, в который время от времени заходят покупатели. При определённых допущениях время между появлениями двух последовательных покупателей будет случайной величиной с экспоненциальным распределением. Среднее время ожидания нового покупателя (см. ниже) равно . Сам параметр тогда может быть интерпретирован как среднее число новых покупателей за единицу времени.

В этой статье для определённости будем предполагать, что плотность экспоненциальной случайной величины задана первым уравнением, и будем писать: .

Функция распределения

Интегрируя плотность, получаем функцию экспоненциального распределения:

Моменты

Несложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:

,

откуда получаем все моменты:

.

В частности,

,

,

.

Отсутствие памяти

Пусть . Тогда .

Пример. Пусть автобусы приходят на остановку случайно, но с некоторой фиксированной средней интенсивностью. Тогда количество времени, уже затраченное пассажиром на ожидание автобуса, не влияет на время, которое ему ещё придётся прождать.

Связь с другими распределениями

• Минимум независимых экспоненциальных случайных величин также экспоненциальная случайная величина. Пусть 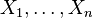независимые случайные величины, и . Тогда

.

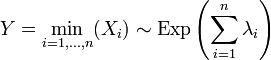Экспоненциальное распределение является частным случаем Гамма распределения:

.

Сумма независимых одинаково распределённых экспоненциальных случайных величин имеет Гамма распределение. Пусть независимые случайные величины, и .

Тогда

.

Экспоненциальное распределение может быть получено из непрерывного равномерного распределения методом обратного преобразования. Пусть . Тогда

.

Экспоненциальное распределение с параметром — это частный случай распределения хи-квадрат:

.

Обозначение
Параметры	- интенсивность или обратный коэффициент масштаба
Носитель
Плотность вероятности
Функция распределения
Математическое ожидание
Медиана
Мода
Дисперсия
Коэффициент асимметрии
Коэффициент эксцесса
Информационная энтропия
Производящая функция моментов
Характеристическая функция

Показательно распределение

Плотность вероятности.

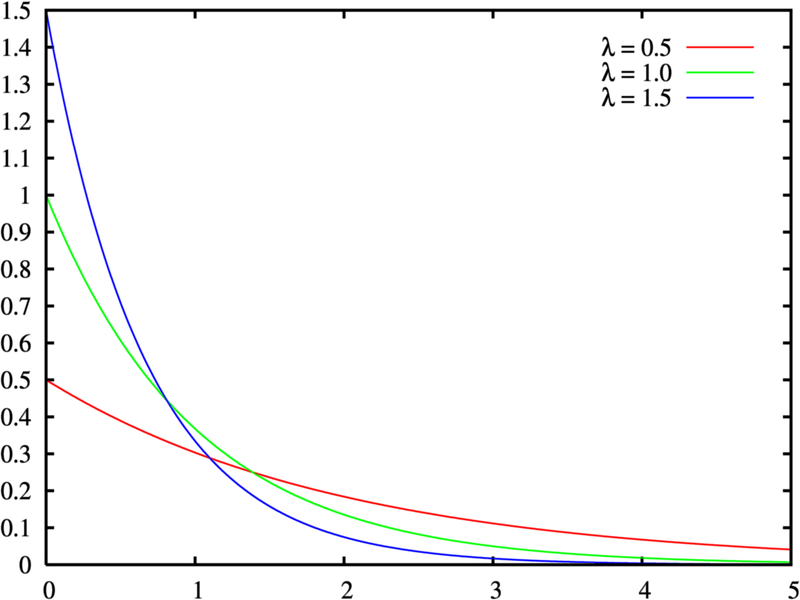
Функция распределения

Источник: http://ru.wikipedia.org

Сущность дисперсионного анализа. Понятие о факторной и остаточной дисперсиях.

Дисперсионный анализ — это статистический метод оценки связи между факторными и результативным признаками в различных группах, отобранный случайным образом, основанный на определении различий (разнообразия) значений признаков. В основе дисперсионного анализа лежит анализ отклонений всех единиц исследуемой совокупности от среднего арифметического. В качестве меры отклонений берется дисперсия (В)— средний квадрат отклонений. Отклонения, вызываемые воздействием факторного признака (фактора) сравниваются с величиной отклонений, вызываемых случайными обстоятельствами. Если отклонения, вызываемые факторным признаком, более существенны, чем случайные отклонения, то считается, что фактор оказывает существенное влияние на результативный признак.

Для того, чтобы вычислить дисперсию значения отклонений каждой варианты (каждого зарегистрированного числового значения признака) от среднего арифметического возводят в квадрат. Тем самым избавляются от отрицательных знаков. Затем эти отклонения (разности) суммируют и делят на число наблюдений, т.е. усредняют отклонения. Таким образом, получают значения дисперсий.

Важным методическим значением для применения дисперсионного анализа является правильное формирование выборки. В зависимости от поставленной цели и задач выборочные группы могут формироваться случайным образом независимо друг от друга (контрольная и экспериментальная группы для изучения некоторого показателя, например, влияние высокого артериального давления на развитие инсульта). Такие выборки называются независимыми.

Нередко результаты воздействия факторов исследуются у одной и той же выборочной группы (например, у одних и тех же пациентов) до и после воздействия (лечение, профилактика, реабилитационные мероприятия), такие выборки называются зависимыми.

Дисперсионный анализ, в котором проверяется влияние одного фактора, называется однофакторным (одномерный анализ). При изучении влияния более чем одного фактора используют многофакторный дисперсионный анализ (многомерный анализ).

Факторные признаки — это те признаки, которые влияют на изучаемое явление. Результативные признаки — это те признаки, которые изменяются под влиянием факторных признаков.

Для проведения дисперсионного анализа могут использоваться как качественные (пол, профессия), так и количественные признаки (число инъекций, больных в палате, число койко-дней).

Методы дисперсионного анализа:

1. Метод по Фишеру (Fisher) — критерий F (значения F см. в приложении N 1); Метод применяется в однофакторном дисперсионном анализе, когда совокупная дисперсия всех наблюдаемых значений раскладывается на дисперсию внутри отдельных групп и дисперсию между группами.

2. Метод "общей линейной модели". В его основе лежит корреляционный или регрессионный анализ, применяемый в многофакторном анализе.

Обычно в медико-биологических исследованиях используются только однофакторные, максимум двухфакторные дисперсионные комплексы. Многофакторные комплексы можно исследовать, последовательно анализируя одно- или двухфакторные комплексы, выделяемые из всей наблюдаемой совокупности.