Понятие сходимости алгоритмов обучения (алгоритмов проектирования адаптивной системы) или устойчивости обучающихся систем.

Т

езис о сходимости или устойчивости здесь точно такой же. Обычное понятие сходимости нам ничего не дает:

т. к. имеется случайные воздействия в виде вектора , то значит значение у нас тоже случайное. И мы можем совершенно необязательно сойтись к этому оптимуму .

Поэтому просто перечислим различные виды сходимости, известные в математике:

а) Сходимость по вероятности. Будем говорить, что 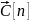по вероятности сходится к , если для любого, сколько угодно малого положительного ε предел:

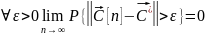
v

Это очень слабое требование. Вероятность равна 0, это вовсе не означает, что событие может не наступить. Можно получить маленькое расхождение между векторами и будет обратное выражение (< ).

б) Сходимость в среднеквадратичном.

Б

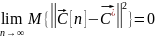
удем говорить, что вектор сходится к вектору среднеквадратичном, если матожидание от квадрата от нашей нормы при увеличении n равно 0:

П

v

оскольку всегда берется квадрат (мощность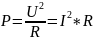 ), то этот критерий называется энергетическим критерием, он часто используется в теории фильтрации.

Этот вид сходимости включает в себя и сходимость по вероятности. Но, опять-таки, вовсе не предполагает классической сходимости, не дает полной гарантии, что вектора у нас полностью сойдутся.

в) Сходимость «почти наверное» (с вероятностью 1).

Б

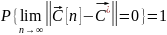
удем говорить, что сходится к «почти наверное», если вероятность обычной сходимости = 1. Т. е.:

Вот такие виды сходимости используются для оценки устойчивости или сходимости систем обучения.

Критерии сходимости алгоритмов обучения.

1. Дискретный алгоритм.

Выпишем его:

*

К сожалению, мы не можем взять, поскольку он нам нужен для накопления, нужен сигнал сам в этом времени, потому берем на предыдущем шаге .

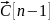Д

*

ля того, чтобы алгоритм сходилась «почти наверное» необходимо, очевидно, чтобы правая часть стремилась к 0 с ростом n. То есть:

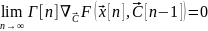
Однако в силу случайности реализации, это необязательно равно 0, значит необходимо, чтобы Г [n] → 0. Примем без доказательства.

П

*

ерейдем к достаточным условиям:

Для того, чтобы дискретный алгоритм обучения сходился «почти наверное», достаточно, чтобы:

1. К

   

   ритерий проектирования: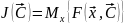

при возрастании (с увеличением) рос не быстрее, чем квадратичная парабола.

2. Э

   

   лементы диагональной матрицы Г [n] удовлетворяли бы условиям Роббинса–Монро: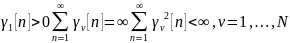

Дадим геометрический смысл:

J

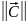
Высокие производные этого критерия, если критерий очень грубо задирается при возрастании , если он сильно отличается от оптимального, то тогда получается стекающий алгоритм.

Судя по рисунку мы берем лекало квадратичной параболы - - - -, и у нас критерий возрастать должен не быстрее, не круче, чем лекало квадратичной параболы, а пойти он может как показано на рисунке двумя разными способами. Тогда у нас алгоритм будет брать не очень высокую производную, и у нас не будет больших пиков, аномалий, с которыми мы боролись в курсовом проекте по «Методам оптимизации», раскачивания не будет. Это не сильное ограничение, самое главное – крутизна возрастаний.

Теперь Роббинса–Монро:

Система у нас с обратной связью, а если вспомнить теорию управления, там берется минус, если мы возьмем неположительную Г, связь окажется положительной обратной связью. А системы с положительной обратной связью из теории управления известно, что неустойчивы, малейшее отклонение приводит к увеличению ошибки.

Первое условие: обеспечивает отрицательность обратной связи. Только системы с ООС (отрицательной обратной связью) устойчивы.

А два других условия говорят нам о следующем:

Скорость изменения коэффициентов γ – элементов матрица Г, должна быть такой, чтобы использовать достаточно большое количество наблюдений то есть она не должна быстро затухнуть:

но и чтобы с ростом n влияние случайностей нивелировалось:

Г

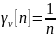армонический ряд: – удовлетворяет условиям Роббинса–Монро.

Вроде бы данные суммы должны затухать, действительно до бесконечности он будет равен бесконечности, все время будет накапливаться. Но это уже инженерия, инженерный подход: γ вовсе можно не изменять по такому закону с самого начала. Если мы отложим – это будет гипербола (1). Мы можем сделать следующее: сначала взять и подержать какое-то время его постоянным, а потом взять и начать уменьшение по гиперболе (2). А чтобы алгоритм вначале вообще шел побыстрее, мы можем сделать так, а потом изменять его по этому закону (3) и т. д.:

(3)

(2)

(1)

То есть, вот эти два условия задают два коридора. С одной стороны γ должно все-таки затухнуть сверху, а с другой стороны оно не должно быстро затухнуть, чтобы дать нам возможность использовать случай. В этом коридоре (4) мы можем работать. Вот что такое управление Роббинса–Монро.

(4)

2. Н

   епрерывные системы.

**

Непрерывный алгоритм обучения сходится в среднеквадратичном, если:

1. Т

   от же критерий проектирования:

При росте норм вектора возрастает побыстрее квадратичная парабола, тоже самое.

2. Э

   

   лемент диагональной матрицы Г (t) удовлетворяет условиям:

Геометрический смысл тот же самый.