Обобщенная формулировка задачи проектирования.

В общем случае показатель качества проектирования можно записать в следующем виде:

J(C₁, C₂, …, C_N) = M_x{F(x₁, …, x_m, C₁, …, C_N)} =

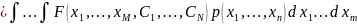
Х

Т. е. в виде матожидания от некоторой известной нам функции F, зависящей от параметров проектирования C₁, C₂, …, C_N и случайных процессов , воздействующих на систему.

Функцию F мы задаем сами. Она выражает требования, цели проектирования.

А поскольку на нее действует случайный вектор, то мы ее усредняем.

О

=

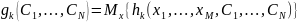граничения записываются в следующем виде:

Х

k = 1… M₁, M₁ < N.

Значения этой функции тоже будут случайными, поэтому мы усредняем их матожиданием

Введем следующее понятие:

- вектор воздействий:

• вектор параметров проектирования:

• вектор – функции, участвующие в формировании ограничений:

Т

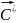
огда задача проектирования может быть сформулирована в общем случае:

Т

ребуется определить значения параметров проектирования , которые минимизируют критерий качества проектирования:

П

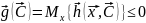
ри следующих ограничениях:

Эта универсальная формулировка охватывает все три типа рассмотренных нами систем. Рассмотрим, во что она выражается:

1. Детерминированная система:

Р(х)

х

Тогда:

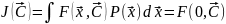
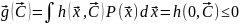
2. Стохастические системы:

P(x) – вероятность менее удобная, но она нам известна. Т. е., например:

Р(х)

х

Тогда постановка задачи такая же, как и в общем виде.

Решение задачи структурно, то же самое, но мы решаем задачу в среднем, и находим в среднем наилучшее решение.

3. Адаптивные системы:

P(x) – некая функция, но нам она неизвестна.

И

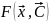
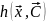
тогда в явном виде мы не можем задать ни критерий, ни ограничения, а задача состоит в нахождении оптимального варианта параметров .

Сделать это можно лишь наблюдая отдельные реализации и .

В данной ситуации это достигается лишь методами обучения или адаптации.

С пособы решения задачи оптимизации и их сущность.

Здесь речь пойдет о том, как нас найти оптимальный вектор .

Р

азличают два класса методов:

- Аналитические (явные) – они дают просто формулу для нахождения . Плюс – получили формулу и подставили, все просто. Минус – для систем выше 3-го, 4-го порядка единой методики решения задач проектирования не существует. Используются другие методы.

-

Алгоритмические методы (численные методы) – задают некий алгоритм или управление некой «машины», при выполнении которого или при движении которой мы получим оптимальное .

Для выяснения сущности алгоритмических методов рассмотрим детерминированную скалярную задачу.

П

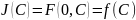
ример: Детерминированная => случайности нет, скалярная => не вектор.

Требуется найти способ отыскания С^*, который даст минимум.

П оложим, что f(C) – непрерывная и минимум один раз дифференцируемая функция. Тогда самый простой способ – взять 1-ю производную от f(C) и приравнять ее к нулю:

f

C

f ’

C

f ’(C) = 0 => C = ?

Е

˅

сли f ’(С) неразрешима относительно С, то поставим себе вопрос – нельзя ли статическую задачу превратить в динамическую? Такую, которая в какие-то моменты времени или в конце своей работы даст нам значение, совпадающее с оптимальным С^*.

f ’(С) = 0 – статическая задача

З

1

апишем следующее уравнение:

Это уравнение, которое заставляет C(t) изменяться со временем. Оно задает изменение параметра C во времени.

Е

сли возьмем γ(t) ≠ 0 (коэффициент усиления «машины»), то если f ’(С(t)) → 0, значит и

(правая часть стремится к нулю => левая тоже).

Т

1

˅

. е. процессы в системе прекратятся в момент f ’(С(t)) = 0. Т. о., представим, что мы соорудили «машину», которая движется в соответствии с уравнением , и в установленном режиме останавливается в точке f ’(С(t)) = 0.

О

1

пределение: Такое преобразование статического уравнения в динамическое уравнение , эквивалентное ему по результату решения, называется в математике навязыванием движения.

Структурная схема такой «машины» будет иметь следующий вид:

f ’(С)

– γ(t)

∫

ФП

У

С₀ = С(0)

С(t)

ИУ

Обозначения: ФП – функциональный преобразователь;

У – усилитель;

1

ИУ – интегрирующий усилитель.

Эту схему можно называть реализацией непрерывного алгоритма . Это способ решения на физических элементах задачи проектирования.

Определение: Такие схемы называют непрерывными алгоритмами или непрерывными методами.

Может быть реализована на стендах, на АВМ и т. д.

Эта «машина» автономна, т. е. извне на нее не действует ничего. Все, что нужно для решения задачи: цель, критерии и условия проектирования – заложены в блоке ФП.