Лекция №1 (19.02.14г.)

Автоматизация и проектирование динамических систем. Типы динамических систем. Понятие динамических систем.

Определение: Динамическая система – это система, поведение которой нас интересует во временном аспекте.

Определение: Динамическая система (ДС) – это та, состояние которой в каждый момент времени определяется не только воздействием на нее в этот момент времени, но и некой предысторией. Поэтому такие системы называются иногда системами с памятью.

Под классификацией динамических систем мы будем понимать классификацию моделей динамических систем. А модель отражает те аспекты в поведении системы, которые нас интересуют в данный момент.

В качестве независимых переменных в ДС всегда выбирают время.

Классификация динамических систем:

В СДС есть время и отсчеты времени, которые определяются некими событиями. И нас интересует состояние системы только в эти моменты времени.

Классические пример динамической системы – очередь.

В СДС заранее моменты времени нам неизвестны, а точки отсчета определяются событиями.

Тут используется аппарат математических аппаратов, GPSS и т. д.

В НДС нас интересует поведение системы при непрерывной оси времени.

В

t

НДС используется продукт WinMass, SSMP и т. д.

В НСДС моменты времени определялись событиями, но также интересовала нас динамика между событиями.

Очень развивалось это направление на кафедре ВТ МЭИ до перестройки, но данное направление остановилось и не имело дальнейшего развития. (Kindler «Языки моделирования»).

НДС условно делится на два класса – системы с сосредоточенными параметрами (НДССП) и НДС с распределенными параметрами (НДСРП).

В НДСРП, кроме независимых переменных времени есть другие независимые переменные, например, пространство.

Представим задачу по физике: стена, к которой приставлен стержень. Координата по стержню – х.

Надо найти распределение температуры по стержню:

x

T

t

В момент времени t₀ повышаем температуру Tº стены => стержень тоже прогревается постепенно (изменение серым цветом линии).

Ось времени будет направлена в сторону, т. к. температура будет изменяться по времени, и по координате х.

Решение таких систем происходит при помощи дискретизации (метод сеток) по х, и получается много связанных элементов стержня. Больше кусков => точнее решение.

Либо можно решать уравнения с параметрами. Для данной задачи уравнения имеют следующий вид:

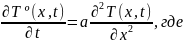
a – характеристика теплоемкости.

Таким уравнением описывается поведение стержня. Нас интересует 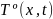- ? Т. е. изменение температуры стержня во времени и пространстве.

Нужно задать начальные условия:

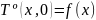
Обычно задают:

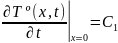
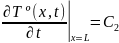
(или ∞)

Получили так называемое параболические уравнения. Технология решения их сложна, единой методики решения не существует, для каждого случая подбирается свой метод решения чисто на интуитивном уровне, на уровне абстракции и интеллекта, затем проверяется подходит данный метод решения или нет.

Но мы не будем рассматривать класс НДСРП – моделей.

НДССП делится на НДС и ЦДС. Для НДС аппаратом служат обыкновенные дифференциальные уравнения. Для ЦДС используют обыкновенные разностные уравнения.

Пример:

Рассмотрим инерционное звено:

*

x – входная величина,

y – выходная величина.

T – инерционная постоянная времени

k – коэффициент усиления.

Задаем начальные условия:

Нас интересует

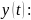
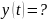
Э

**

то непрерывное уравнение.

А: 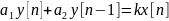– это цифровое уравнение.

Мы задаем 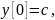и смотрим, как изменяется 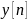при изменении n.

Когда мы будем говорить о вычислениях на ЭВМ, будем говорить о ЦДС.

(В начале, когда воздействие х только появилось, оно разложилось между выходом (y) и производным воздействием. А затем в конце, когда система изменила свое положение, состояние и т. д. производная равна нулю.

В ЦДС воздействие раскладывается между предыдущим состоянием и текущем состоянием, и на текущее воздействует то, что было на предыдущем шаге.

В этом и состоит динамика – положение и состояние системы на предыдущем моменте времени влияет на текущей момент).

Частным случаем динамической системы является статика. Мы убираем члены уравнения, описывающие предыдущий момент времени. Тогда поведение системы в каждый момент времени будет зависеть только от внешнего воздействия.

В ЦДС:

Δt называются интервалами дискретизации, они заранее известны и постоянны, в отличии от НСДС.

М

**

*

ежду уравнениями и существует связь.

Теорема о предельном переходе:

От разностных уравнений мы можем перейти к непрерывным, устремив интервал дискретизации к нулю. И наоборот, можно перейти к разностному уравнению, проведя дискретизацию.

(Цифровые часто будем называть дискретными ДС).

Мы будем рассматривать класс НДССП.

В

С

(система)

общем случае дискретную систему можно представить следующей диаграммой:

→

→

f y

→

x

→

→

g

f

→

– вектор управляющих воздействий, который мы сознательно подаем

y

→

– вектор реакций, выходные величины

g – вектор случайных воздействий

М

→

→

→

ожно записать, что:

y

→

= G( f, g, t) , то есть вектор реакций представляет собой некий функционал от управляющих воздействий, случайных воздействий (дрейф, ветер и т. д.) и времени.

О

→

чень часто вектор возмущений (случайных воздействий) объединяется с вектором f и считают, что на систему воздействует вектор x, который будет в общем случае случайным, так как включает случайные компоненты.

Типы систем по уровню априорной информации.

Теперь мы уже говорим только о классе НДССП.

1. Д етерминированные системы – системы с полной априорной информацией относительно условий ее работы и предъявляемых к ней требований.

x(t) – известное воздействие,

y(t) – наблюдаемая реакция,

y₀(t) – установка, идеальное (желаемое) поведение,

ε(t) – ошибка (невязка).

В реальных условиях имеют место:

- внутренние помехи (шум, дрейф, температура);

- внешние помехи (треска, температура, скачок напряжения и т. д.), т. е. неконтролируемые нами воздействия, носящие случайный характер.

Мы должны учитывать внешние помехи => приходим к следующему типу систем.

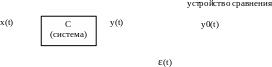2. С тохастические системы характеризуются тем, что нельзя говорить о точном значении величин в какой-то момент времени, а можно лишь указать вероятность, что она примет значение.

~

~

~

(символ ~ означает, что это случайная величина).

Невязка получается случайной величиной, поэтому ее характеризуют вероятностными характеристиками:

- Математическое ожидание M { ε(t) }

- Дисперсия (среднеквадратическое отклонение от нуля для центрированного процесса)

M {( ε(t) – M { ε(t) })²} – это в общем виде.

M {( ε²(t) } – для центрированного процесса.

- Вероятность P { ε < α } – вероятность того, что ε < α.

Априорная информация в данных системах меньше, мы знаем лишь среднее значение процессов, т. е. можно получить лишь среднее значение процессов.

Источником случайности ε(t) является то, что входное воздействие x(t) является случайным.

В общем случае, математическое ожидание можно выразить следующим образом:

X

M { ε(t) } = ε(x) P(x) dx - математическое ожидание по множеству

Для определения всех характеристик надо знать P(x), т. е. стохастические характеристики наших случайных воздействий.

Если они неизвестны, то есть какие-то реализации процессов есть, но нет статистики поведения процессов (или пока нет), то мы приходим к третьему виду систем.

3. Адаптивные системы (обучающиеся системы) – улучшают показатели своего функционирования в процессе этого функционирования.

Т. е. в нашем случае имеется текущая, или рабочая информация, извлекаемая из любых сигналов, и идея построения адаптивной системы может быть сформулирована как: путем надлежащей обработки текущей информации компенсировать недостаток априорной информации.