- •Теоретическая механика
- •Пермь 2014
- •Методические указания
- •Рабочая программа
- •Список учебной литературы основной
- •Дополнительный
- •Контрольные задания
- •Порядок выполнения работ, пояснения к тексту задач
- •Задачи к контрольным заданиям статика
- •Задача с1
- •Задача с2
- •Кинематика
- •Задача к1 (тема: “Кинематика точки”)
- •Задача к2 (тема: “Кинематика плоского механизма”)
- •Динамика
- •Задача д1 (тема: “Динамика точки”)
- •При найденном значении c2 , уравнение (11) дает
- •Задача д3 (тема: “Теорема об изменении кинетической энергии системы”)
- •Задача д4 (тема: “Принцип возможных перемещений”)
- •Задача д6 (тема: “Принцип Даламбера для механической системы”)
Задачи к контрольным заданиям статика
В статике рассматривается а) теория сил, б) равновесие тел под действием различных систем сил. Все задачи контрольного задания (С1-C3) относятся к теме о равновесии. Это позволяет привести общие для всех задач сведения справочного характера из теории и сформулировать алгоритм решения задач.
ВИДЫ СВЯЗЕЙ
Связь – тело, препятствующее перемещению данного объекта (тела, узла) в пространстве. Реакция связи – сила, с которой связь действует на объект.
Вид связи |
Направление реакции связи |
Гладкая поверхность, на которую объект опирается в точке A.
|
Реакция гладкой поверхности в точке A направлена по нормали к поверхности опоры. |
Острие, угол, линия (гладкие).
|
Реакция
|
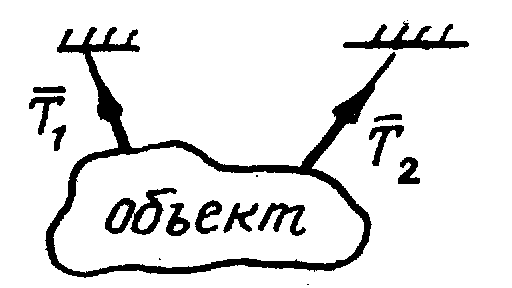
Гибкая связь (трос, цепь, нить).
|
Реакция гибкой связи направлена вдоль связи от объекта (нить растянута). |
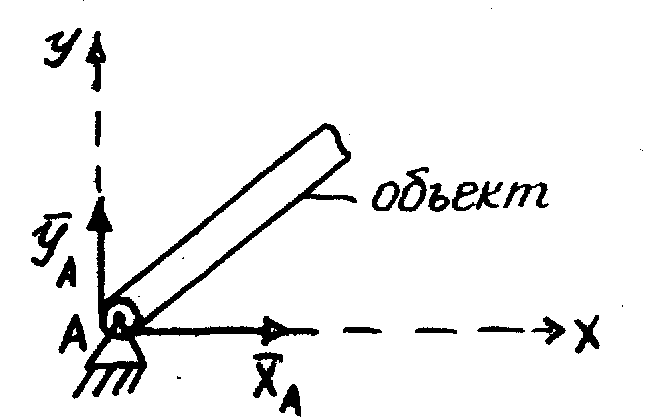
Цилиндрический неподвижный шарнир.
|
Реакция
цилиндрического шарнира в точке A
расположена в плоскости, перпендикулярной
оси шарнира; направление в плоскости
не определено, указываем составляющие
реакции шарнира по координатным осям:
|
Катки (подвижный шарнир) без трения.
|
Реакция связи направлена по нормали к поверхности опоры катков. |
Невесомый стержень, концы которого закреплены шарнирами.
|
Реакция связи направлена вдоль прямой, проходящей через концы стержня. Указываем от объекта, предполагая, что стержень растянут; минус в ответе означает, что стержень сжат. |
Подшипник B и подпятник A (сферический шарнир A).
|
Pеакция
подшипника B
расположена в плоскости, перпендикулярной
оси подшипника (ось z);
указываем в плоскости две составляющие
этой реакции по коорд. осям:
Направление
реакции подпятника A
в пространстве не определено; указываем
в пространстве три составляющие этой
реакции по коорд. осям:
,
,
|
В плоскости
В пространстве
|
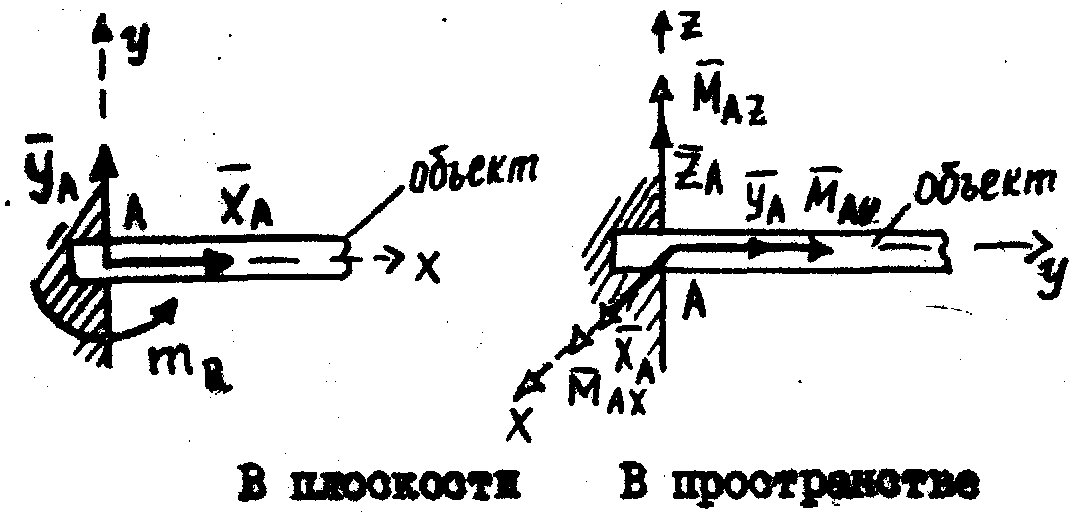
В случае плоской системы сил на объект действует сила, направление которой в плоскости действия сил не определено, и пара сил в этой плоскости. В случае пространственной системы сил на объект действует сила, направление которой в пространстве не определено, и пара сил, направление вектора момента которой в пространстве не определено (см. рис.). |
ОСНОВНЫЕ ПОНЯТИЯ
линия действия
силы |
Сила, действующая на твердое тело – скользящий вектор |
|
Проекция силы на ось
|
|
Проекция силы на плоскость
|
|
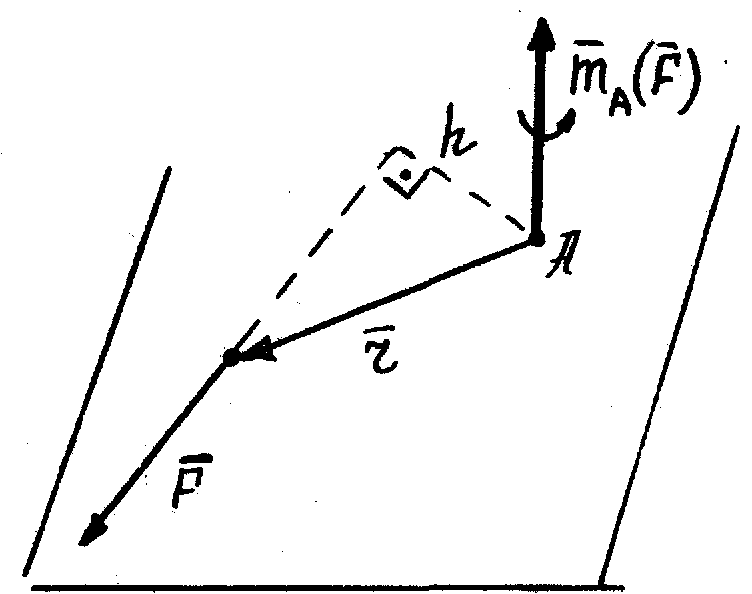
Момент силы относительно центра (точки) как вектор:
алгебраическое значение этого момента:
Знак
h – перпендикуляр, опущенный из центра А на линию действия силы (плечо силы) |
|
Момент силы относительно оси
перпендикулярную оси; А – точка пересечения оси с этой же плоскостью;
h
– плечо
силы
|
плоскость
действия пары сил
|
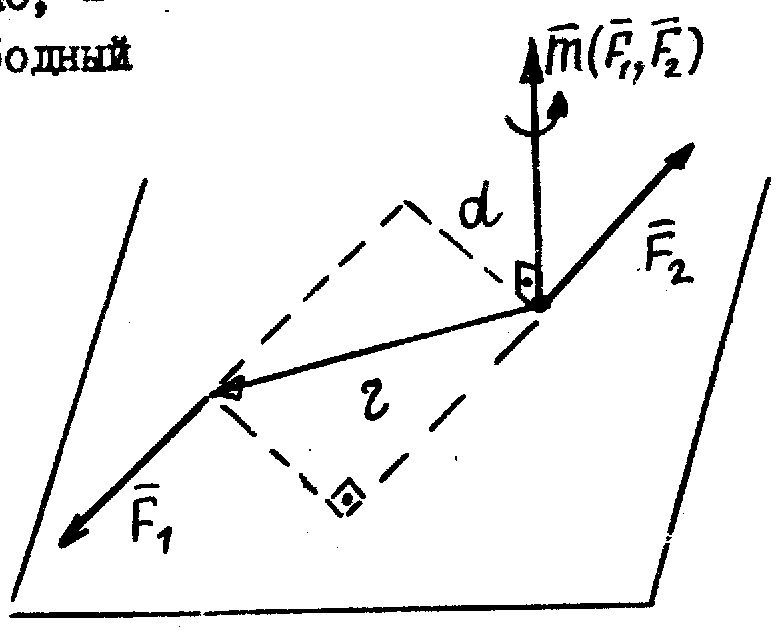
Пара
сил
|
|
Действие
пары сил полностью характеризуется
вектором-моментом пары сил
Момент пары сил, действующей на твердое тело, – свободный вектор. Алгебраическое значение момента пары сил:
|
ВИДЫ СИСТЕМ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО,
И УРАВНЕНИЯ РАВНОВЕСИЯ
O
O
O
|
Векторная форма:
Координатная форма (аналитическая): |
|
1.
2.
3.
|
4.
5.
6. |
|
|
Векторная форма:
Координатная форма: 1. ; 2. ; 3. (для равновесия сходящейся системы сил необходимо и достаточно, чтобы сумма проекций сил на каждую ось была равна нулю). |
|
O
O
|
Векторная форма: .
Координатная
форма (ось
1. 2. ; 3. . |
|
y
x
F1
F2
F3
F4
F5
A
O
B
С |
Векторная форма: . Координатная форма: 1-я форма (точка А – произвольная точка в плоскости):
1.
;
2.
;
3. 2-я форма (точки A, B, С не лежат на одной прямой):
1.
;
2. 3-я форма (Ось ОХ не перпендикулярна прямой АВ): 1. ; 2. ; 3. |
|
x
y
F1
F2
F3
F4
F5
O
A
|
Векторная форма: . Координатная форма (ось Х параллельна линиям действия сил): 1. ; 2. . |
|
Примерный план (алгоритм) решения задач статики:
Назвать (выделить) объект: тело, узел, равновесие которого надо рассмотреть в данной задаче.
Указать на рисунке силы, действующие на этот объект:
а) активные силы;
б) назвать каждую связь и пояснить направление реакций связи или их составляющих (мысленно освобождая объект от связи на основании аксиомы освобождения от связей);
Назвать вид полученной системы сил, учитывая расположение линий действия сил.
Сформулировать условия равновесия полученной системы сил в алгебраической (координатной) форме.
Провести на рисунке координатные оси (если заранее не потребовалось это сделать).
Составить уравнения равновесия.
Решить систему уравнений с пояснением.
Сделать проверку.
Записать ответ.
При работе необходимо использовать учебник, данное пособие и справочник по математике.



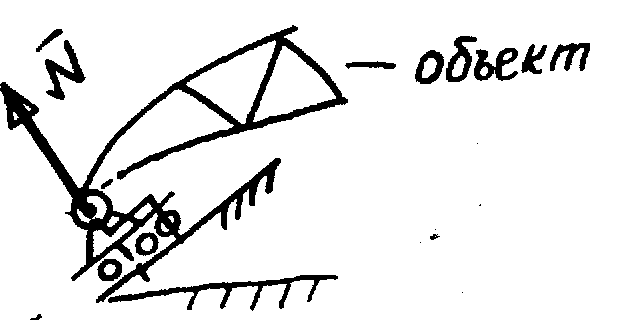
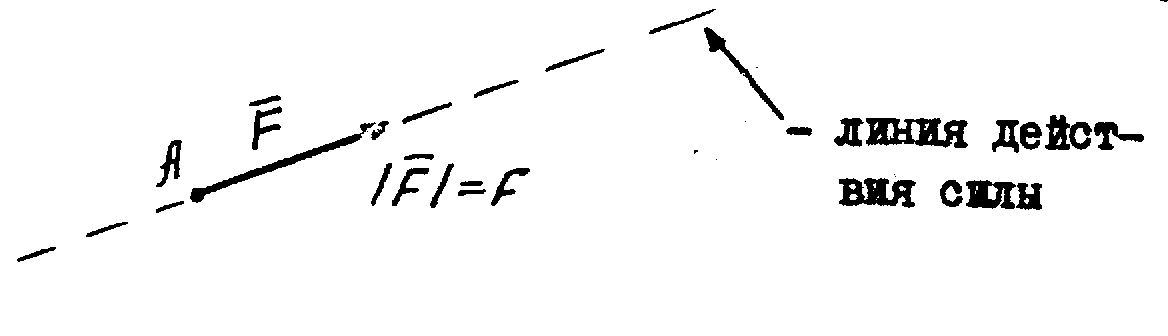


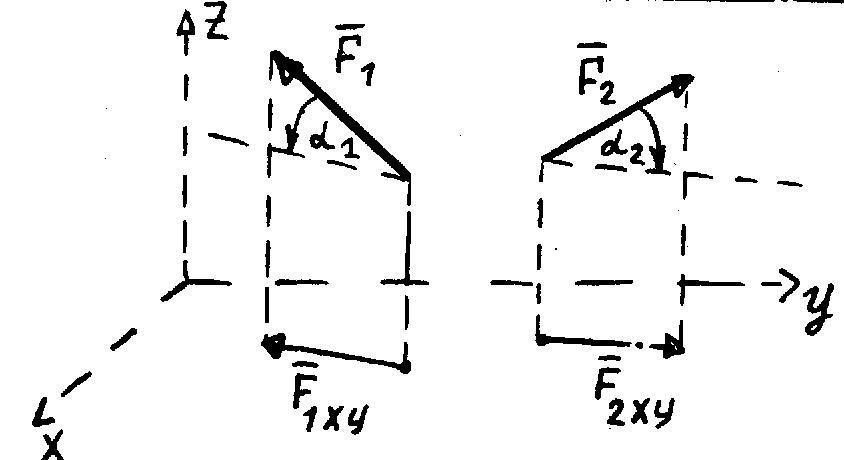



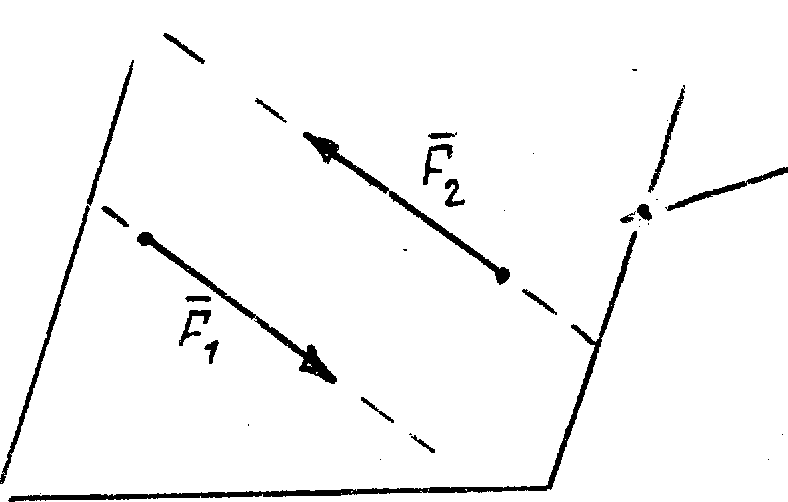





 Система
сходящихся сил – линии действия сил
пересекаются в одной точке.
Система
сходящихся сил – линии действия сил
пересекаются в одной точке.