МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»

Институт кибернетики информатики и связи

Кафедра Электроэнергетики

Сравнительный анализ методов решения сложных разветвленных электрических цепей

Методические указания к контрольной работе

по дисциплине «Электротехника»

для студентов заочной и заочной сокращенной формы обучения неэлектрического направления

Составитель А.П. Пожитков,

ассистент

Тюмень

ТюмГНГУ

2013

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ 4

Библиотечно-издательский комплекс 20

Типография библиотечно-издательского комплекса. 20

ВВЕДЕНИЕ

Дисциплина «Электротехника» относится к циклу общепрофессиональных дисциплин и имеет своей целью формирование знаний у студентов в области теории электрических цепей и электромагнитного поля.

Процесс освоения дисциплины включает в себя:

1. изучение основных понятий и законов электричества и магнетизма, теории функций комплексного переменного, векторного анализа

2. изучение методов дифференциального и интегрального исчисления для расчета электрических и магнитных цепей;

3. изучение методов формализации процессов составления уравнений электрического равновесия сложных электрических цепей;

В результате освоения дисциплины студент должен:

1. знать основные законы определения и понятия теории электрических цепей;

2. уметь выполнять расчеты параметров электротехнических установок, установившихся и переходных процессов в линейных и нелинейных цепях, электрического поля постоянного тока, магнитного поля постоянного тока, электромагнитного поля;

3. владеть навыками составления уравнений электрического равновесия сложных электрических цепей.

Целью данной контрольной работы является закрепление знаний у студента основных понятий и законов теории электрических цепей. Выполнение работы позволит студенту выработать навыки составления уравнений электрического равновесия для расчета сложных многоконтурных электрических цепей постоянного тока.

1. Методы расчета Сложных разветвленных электрических цепей

1. Составление уравнений по законам Кирхгофа

Рассмотрим пример составления уравнений по законам Кирхгофа для представленной электрической схемы (рис. 1.1)

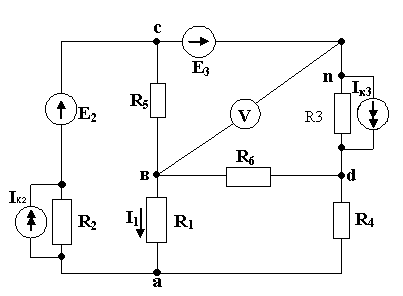
Рис. 1.1. Исходная электрическая схема

Преобразовываем источники токов в источники напряжения.

; .

Выбираем условно-положительные направления сил токов и направления обхода контуров (рис. 1.2).

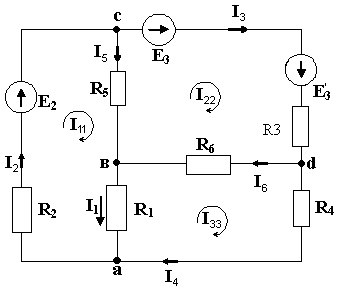
Рис. 1.2. Преобразованная электрическая схема

I закон Кирхгофа.

Алгебраическая сумма токов в узле равна нулю:

(1)

При составлении уравнений по первому закону Кирхгофа требуется составить n-1 уравнений, где n – это количество узлов в схеме.

;

;

;

Если сила тока направлена к узлу, то в формуле перед ней стоит знак «+», если же сила тока течет от узла, то в формуле перед ней ставится знак «-».

II закон Кирхгофа.

Алгебраическая сумма падений напряжений вдоль замкнутого контура равна алгебраической сумме ЭДС, действующей в этом контуре:

(2)

В схеме выбираются независимые контуры и на основе выбранных направлений обхода контура составляются уравнения.

;

;

.

Если направление силы тока или ЭДС совпадает с направлением обхода контура, то в уравнении перед соответствующим слагаемым ставится знак «+», если нет, то знак «-».

2. Метод контурных токов

Метод основан на уравнениях, составленных по второму закону Кирхгофа. Суть метода в том, что в каждом независимом контуре в схеме протекает свой так называемый контурный ток.

Произвольно выбираются направления контурных токов в независимых контурах (см. рис. 1.2) и относительно них составляются уравнения по второму закону Кирхгофа.

;

;

.

Собственное сопротивление контура — сумма сопротивлений, входящих в состав контура, например для второго контура – (R₃+R₅+R₆).

Смежные сопротивления — сопротивления на границах контуров (для второго контура – R₅ и R₆).

Если на смежных ветвях контурные токи совпадают по направлению, то перед смежным током ставится знак «+», если не совпадают, то – «-».

Полученная система уравнений решается любым удобным математическим способом, например матричным методом.

; ; .

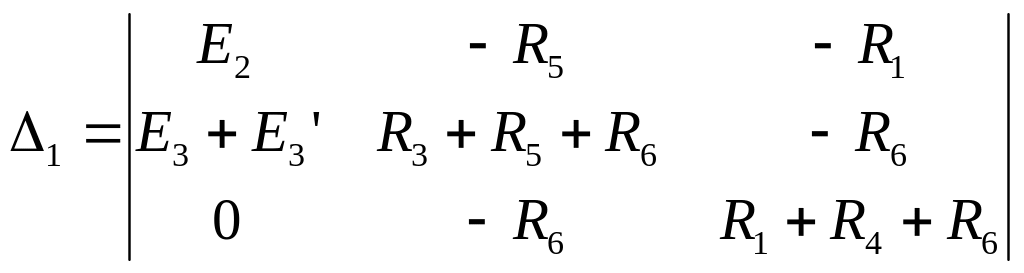
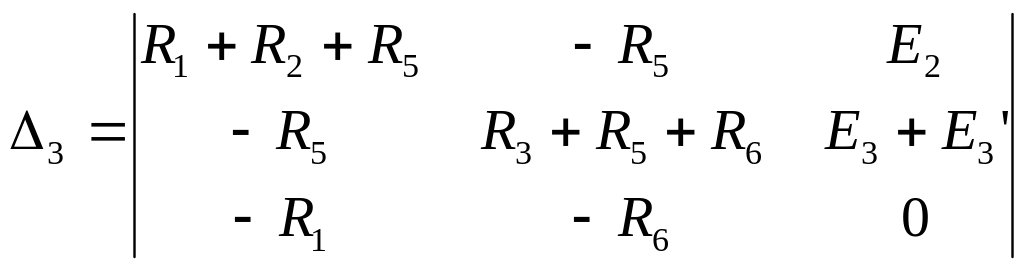
Полученные контурные токи используются для расчета токов в ветвях.

3. Метод узловых потенциалов

Метод узловых потенциалов основан на уравнениях первого закона Кирхгофа. Потенциал одного из узлов принимается равным нулю. Такое предположение допустимо, так как ток в каждой ветви зависит не от абсолютных значений потенциалов узлов, а от разности потенциалов, приложенной к ветви.

Пусть потенциал узла «d» равен нулю.

Токи в ветвях выражаются на основании закона Ома

,

где – напряжение на зажимах ветви. Знаки перед U_ab и Е выбираются в зависимости от того, совпадает или не совпадает направление тока I с положительными направлениями U_ab и Е.

Таким образом, токи в ветвях равны:

;

;

;

;

;

.

Y₁ – Y₆ — проводимости соответствующих ветвей.

Полученные выражения для токов подставляем в исходную систему уравнений, составленную по первому закону Кирхгофа.

;

;

;

После некоторых математических преобразований получаем систему уравнений относительно неизвестных потенциалов , , .

;

;

.

Потенциал основного узла умножается на сумму проводимостей всех ветвей образующих данный узел (для узла «с»— это , , ). Потенциалы смежных узлов умноженные на проводимость соответствующих смежных ветвей записываются в уравнении со знаком «-».

В правой части уравнения слагаемые вида записываются со знаком «+», если источник ЭДС направлен к рассматриваемому узлу, в противном случае – со знаком «-».

Найденные потенциалы подставляются в выражения, составленные для сил токов по закону Ома.