14. Операції над функціями вибору.

Функція вибору вкладається у функцію вибору ( ), якщо для .

Об'єднанням ФВ і називається функція вибору , що визначається : для .

Перетин визначається : для .

Доповненням до ФВ C називається функція , для якої: , .

Композицією функцій вибору і називається функція вибору , що визначається рівністю: для . Змістовно операція полягає у наступному. Спочатку відбувається вибір у відповідальності з функцією вибору , а потім з відбувається вибір за функцією . Так, з десяти кандидатів у президенти спочатку вибираються двоє, потім вибирається один.

15. Властивості функцій вибору.

1. Умова спадковості (СП): .

2. Умова незалежності від відкинутих альтернатив (умова Неша – Н): .

3. Умова згоди (З): .

4. Умова незалежності вибору від шляху (умова Плотта – П (квазісуматорність)): .

5. Умова суматорності (СМ): .

6. Умова мультиплікаторності (МП): .

7. Умова монотонності (М): .

Теорема 3.7. Функція вибору C є:

1) спадковою;2) незалежною від відкинутих альтернатив; 3) що задовольняє умові згоди; 4) квазісуматорною; 5) суматорною; 6) мультиплікаторною; 7) монотонною; тоді і лише тоді, коли для :

1) ;

2) ;

3) ;

Розглянемо випадок n=2:

4)

;

5) ;

6) ;

7) .

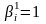Доведення безпосередньо випливає із представлення відповідних умов з допомогою бульових функцій, що утворюють логічну форму. Для прикладу приведемо доведення умови 1. Із умови спадковості отримуємо: . Якщо , то маємо тотожність , якщо , то 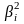= 1 і маємо нерівність: .

Функція вибору C називається:

• рефлексивною, якщо для ;

• антирефлексивною, якщо для ;

• повною, якщо , для ;

• транзитивною, якщо з умови: , випливає , , ;

• ациклічною, якщо з умови: , , випливає: для , .

Теорема 3.9. Функція вибору C є: 1) рефлексивною; 2) антирефлексивною; 3)повною; 4) транзитивною; 5) ациклічною тоді і лише тоді, коли для :

1) ; 2) ; 3) для ; 4) , , ; 5) , , , .

16. Оптимум Парето, оптимум лексиміна.

Ситуація домінує за Парето ситуацію , якщо:

(1.3)

. (1.4)

Ситуація називається Парето-оптимальною (оптимальною за Парето, ефективною), якщо вона не домінується за Парето.

Коротко умови (1.3), (1.4) будемо описувати, як xPy, тоді умова ефективності запишеться як: , , .

Отже, ситуація є ефективною, якщо не існує іншої ситуації, у якій усі гравці мають значення виграшу, не гірші, ніж у , і хоча б один гравець має краще значення функції виграшу. Множину Парето-оптимальних ситуацій позначатимемо РО.

17 . Конфлікти та компроміси, рівновага в домінуючих стратегіях, недоміновані стратегії, обережні стратегії, складна рівновага.

Визначення Стратегія i-го гравця називається недомінованою, якщо не існує стратегії , яка б її домінувала: . Множину недомінованих стратегій i-го гравця позначатимемо через .

Визначення Ситуація називається рівновагою у домінуючих стратегіях, якщо є домінуючою стратегією кожного гравця ( ). Множина називається множиною рівноваг у домінуючих стратегіях.

Стратегія називається обережною (песимістичною) стратегією і-го гравця, якщо

.