
- •Загальна схема прийняття рішень
- •Діаграма Томаса-Кілмана.
- •Задача колективного приняття рішень.
- •Утилітаризм та егалітаризм. Дилема «рівність-ефективність».
- •Прийняття рішень в умовах невизначеності.
- •Прийняття рішень в умовах ризику.
- •Вибір голосуванням, функція колективної переваги, методи голосування.
- •Властивості методів голосування, парадокси голосування.
- •Парадокс Ерроу.
- •10. Функції вибору, нормальні функції вибору
- •11. Критерій нормальності функцій вибору.
- •12. Класи функцій вибору, теорема Черноффа.
- •13. Логічна форма функцій вибору.
- •14. Операції над функціями вибору.
- •15. Властивості функцій вибору.
- •17 . Конфлікти та компроміси, рівновага в домінуючих стратегіях, недоміновані стратегії, обережні стратегії, складна рівновага.
- •18. Рівновага Неша, теорема Неша. Сильна рівновага Неша.
- •19. Критерії вибору Нешівських рівноваг.
- •21. Переговорна множина
- •22. Рівновага Штакельберга
- •23. Кооперативна гра. Принцип відокремлення
- •24. Шеплі
- •26. Задача багатокритеріальної оптимізації. Оптимальні за Парето та Слейтером розв'язки
- •27.Метод ідеальної точки, послідовних поступок, бажаної точки.
- •28.Обробка експертної інформації. Загальна схема експертизи. Методи круглого столу, мозкової атаки, Делфі.
- •29. Статистичні методи
- •30. Алгебраїчний метод
- •31. Нечіткі множини, операції над ними, нечіткі відношення.
- •32. Нечіткі задачі багатокритеріальної оптимізації.
Прийняття рішень в умовах невизначеності.
Потреба в принятті рішень в умовах невизначеності виникає коли альтернатива може привести до множини наслідків.
X – множина альтернатив
Y – множина наслідків
S – множина станів
Формулы есть на листочке, потому что у меня не стоит редактор формул на компе.
Прийняття рішень в умовах ризику.
Потреба в принятті рішень в умовах ризику виникає коли стани появляються з деякою ймовірністю.
X – множина альтернатив
Y – множина наслідків
S – множина станів
p(s) - ймовірність появи стану s
Формулы выписаны на листочке, потому что у меня не стоит редактор формул на компе.
Вибір голосуванням, функція колективної переваги, методи голосування.
Нехай
![]() – множина "виборців",
– множина "виборців",
![]() – множина "кандидатів". Кожен
виборець задає "індивідуальну
перевагу" на множині кандидатів у
вигляді строгого ранжування, тобто
задає лінійний порядок
– множина "кандидатів". Кожен
виборець задає "індивідуальну
перевагу" на множині кандидатів у
вигляді строгого ранжування, тобто
задає лінійний порядок
![]() (повне, транзитивне, асиметричне бінарне
відношення).
(повне, транзитивне, асиметричне бінарне
відношення).
Правило відносної більшості. Перемагає кандидат, за якого голосовала більшість виборців
Правило абсолютної більшості. Перемагає кандидат, за якого проголосовало більш ніж 50% кандидатів.
Правило відносної більшості з вибуванням. У другий тур проходять два кандидата, що набрали відносну більшість голосів у першому турі. У другому турі перемагає той, хто отримав абсолютну більшість голосів.
Правило Борда. Для кожного місця визначається кількість очок, яки отримує за нього кандидат. Перемагає кандидат с найбільшою їх кількістю.
Правило Кондорсе. Переможцем оголошується той кандидат, що перемагає всіх інших у попарних порівняннях.
Правило Копленда. K(a,x) - число виборців, для яких кандидат а кращий за х. Якщо за a голосовало більше виборців, ніж за x, то K(a,x) = +1; інакше K(a, x) = -1; 0 при рівності. Оцінка Копленда кандидата a є
 .
Переможцем Копленда (переможцем за
Коплендом) називається кандидат
(кандидати) з найвищою оцінкою Копленда.
.
Переможцем Копленда (переможцем за
Коплендом) називається кандидат
(кандидати) з найвищою оцінкою Копленда.Правило Сімпсона. S(a,x) – також число виборців, для яких а краще за х. Оцінкою Сімпсона кандидата a називається число
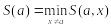 .
Переможцем Сімпсона називається
кандидат (кандидати) з найвищою оцінкою
Сімпсона.
.
Переможцем Сімпсона називається
кандидат (кандидати) з найвищою оцінкою
Сімпсона.Послідовне виключення. Послідовно попарно порівнюються кандидати за правилом більшості. Спочатку перший із вторим, потім переможець із наступим, і так далі.
Паралельне виключення. Кандидати діляться по парам і порівнюються за правилом більшості. Потім теж саме робиться для переможців, поки не залишиться єдиний переможець.
Властивості методів голосування, парадокси голосування.
Аксіома А1 (повнота).
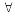
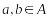 :
:

Аксіома А2 (транзитивність):
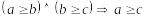 .
.Аксіома А3 (одностайність): якщо для всіх виборців
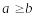 ,
то й у колективному порядку також
,
то й у колективному порядку також
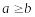 (
(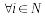 :
:
 ).
).Аксіома А4 (незалежність). Розташування будь-яких двох кандидатів a і b у колективному порядку залежить лише від їх взаємного розташування в індивідуальних порядках і не залежить від розташування інших кандидатів.
Парадокс Ерроу. Якщо голосування задовольняє аксіоми А1-А4, то існує виборець такий, що колективний порядок співпадає х його індивідуальним порядном.
Аксіома А5 (анонімність). Імена виборців не мають значення: якщо два виборці поміняються голосами, то результат не зміниться.
Аксіома А6 (нейтральність). Імена кандидатів не мають значення: якщо поміняти місцями кандидатів a і b у перевазі кожного виборця, то результат голосування зміниться відповідно (якщо раніше вибирався кандидат a, то тепер буде вибиратись кандидат b і навпаки; якщо раніше вибирався деякий кандидат c, відмінний від a і b, то тепер він же і буде вибраний).
Аксіома A3' (ефективність). Якщо кандидат a для всіх виборців кращий за кандидата b, то b не може бути вибраним.
Аксіома А7 (монотонність). Нехай a вибирається при даному профілі й профіль змінюється так, що положення a покращується, а відносне порівняння пари будь-яких кандидатів для будь-якого виборця залишається незмінним. Тоді a для нового профілю також буде вибраним.
Аксіома А8 (поповнення (однозначні правила голосування)). Дві групи виборців
 і
і
 ,
що не перетинаються, вибирають одного
і того ж кандидата a
з множини A.
Тоді виборці з множини
,
що не перетинаються, вибирають одного
і того ж кандидата a
з множини A.
Тоді виборці з множини
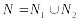 також вибирають a.
також вибирають a.За цією властивістю виборці розбиваються на "територіальні" дільниці або законопроект розглядається у підкомісіях.
Аксіома А'8 (поповнення (відображення голосування)). Нехай виборці з вибирають кандидатів
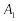 з A,
з
– з
з A,
з
– з
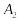 ,
,
 ,
,
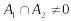 .
Тоді виборці з
виберуть кандидатів з
.
Тоді виборці з
виберуть кандидатів з
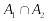 .
.Аксіома А9 (участь). Нехай кандидат
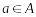 вибирається виборцями з N.
Нехай до множини виборців добавляється
новий виборець i
(
вибирається виборцями з N.
Нехай до множини виборців добавляється
новий виборець i
(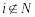 ).
Тоді виборці з
).
Тоді виборці з
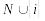 повинні вибрати або a,
або кандидата, який для агента i
є строго кращим a.
повинні вибрати або a,
або кандидата, який для агента i
є строго кращим a.
Аксіома 10 (неперервність). Нехай виборці з вибирають , з –
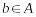 ,
,
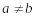 ,
.
Тоді існує (досить велике) натуральне
число m
таке, що
,
.
Тоді існує (досить велике) натуральне
число m
таке, що
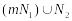 вибере a.
вибере a.
