30. Алгебраїчний метод

Для визначення колективної числової оцінки алгебраїчним методом використовується експертиза 7: , експерти ізольовані, обернений зв'язок відсутній. Відстань між числовими оцінками і визначається як . У якості колективної оцінки приймаються, наприклад, оцінки:

• (утилітарний критерій),

• (егалітарний критерій).

Для визначення колективного ранжування алгебраїчним методом експерти задають матриці , у яких тоді й лише тоді, коли об'єкт передує об'єкту ; якщо об'єкти і рівноцінні або , ; якщо ( ), то .

Ранжування і відповідну йому матрицю будемо позначати одним символом.

Визначення 2.2. Ранжування знаходиться між ранжуваннями і , якщо для або .

Відстань між ранжуваннями вводиться аксіоматично:

А1. , причому ;

А2. (симетричність);

А3. , причому рівність досягається тоді й лише тоді, коли ранжування знаходиться між ранжуваннями і (аксіома трикутника);

А4. При однакових перестановках об'єктів у ранжуваннях і відстань між отриманими ранжуваннями (інваріантність відносно позначень);

А5. Якщо двоє ранжувань відрізняються одне від одного лише на частині об'єктів, то відстань між початковими ранжуваннями дорівнює відстані між ранжуваннями лише цих об'єктів;

А6. Мінімальна додатня відстань між ранжуваннями дорівнює 1.

Теорема 2.3. Аксіоми А1–А6 однозначно визначають відстань (відстань Хемінга) при будь-якій довжині ранжувань , а формула: , визначає єдину відстань , що задовольняє аксіомам А1–А6.

Експертиза 8: {матриці , елементи яких визначені вище}, експерти ізольовані, обернений зв'язок відсутній. У якості відстані береться відстань Хемінга, колективне ранжування визначається критеріями:

• (медіана Кемені–Снелла);

• (компроміс);

• (середнє значення).

Вище – множина матриць з елементами , що відповідають ранжуванням (тобто матриці ациклічні). Як видно – критерій 1 відповідає принципу утилітаризма, критерій 2 – егалітаризма.

Приклад. Нехай 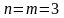, , (позначення означає: ). Випишемо відповідні матриці:

, .

Потрібно знайти медіани 1, 2 на множині матриць, що відповідають ранжуванням: , , . , , . Виписуємо відповідні матриці: , ,

, , , .

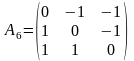Знаходимо:

, ; , ;

, ; , ;

, ; , .

Таким чином, (цього слід було очікувати, оскільки ранжування двох експертів співпали, ранжування третього відрізняються від їх ранжувань лише однією перестановкою). Нехай, , , . Тоді , , .

31. Нечіткі множини, операції над ними, нечіткі відношення.

Нечіткою множиною С на множині Х називається сукупність пар , де , а - функція , що називається функцією належності нечіткої множини С. Значення для конкретного х називається ступенем належності цього елемента нечіткій множині С.

Як видно з цього визначення, нечітка множина цілком описується своєю функцією належності, тому нижче будемо використовувати цю функцію як позначення нечіткої множини. Звичайні множини складають підклас класу нечітких множин. Дійсно, функцією належності звичайної множини є її характеристична функція :

і відповідно до визначення нечіткої множини звичайну множину В можна також визначити як сукупність пар виду . Таким чином, нечітка множина являє собою більш широке поняття, ніж звичайна множина, у тому розумінні, що функція належності нечіткої множини може бути, взагалі кажучи, довільною функцією або навіть довільним відображенням.

Об'єднанням нечітких множин А і В у X називається нечітка множина з функцією належності:

Перетином нечітких множин А і В у X називається нечітка множина з функцією належності , .

Доповненням нечіткої множини А у X називається нечітка множина А' з функцією належності виду

Декартовим добутком у Х нечітких множин називається нечітка множина А з функцією належності виду

Опуклою комбінацією нечітких множин у X називається нечітка множина А з функцією належності виду:

, де .

.Аналогічно "звичайним" бінарним відношенням можна ввести поняття нечіткого бінарного відношення на множині X як нечітку підмножину декартового добутку з функцією належності .

Нехай X – задана множина альтернатив. Нечітким відношенням нестрогої переваги на X будемо називати будь-яке задане на цій множині рефлексивне нечітке бінарне відношення. Оскільки нечітке відношення можна розуміти як нечітку підмножину декартового добутку , то нечітке відношення переваги на множині X будемо описувати функцією належності виду , яка володіє властивістю рефлексивності, тобто .

За заданим на множині X нечітким відношенням переваги можна однозначно визначити три відповідних йому нечітких відношення: байдужності (функцію належності будемо позначати через ), подібності (квазіеквівалентності) і строгої переваги . За аналогією зі звичайними відношеннями переваги ці три відношення можна визначити наступним чином:

де 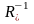– зворотне до відношення , позначається через і описується функцією належності .

1. Нечітке відношення байдужності:

2. Нечітке відношення подібності:

3. Нечітке відношення строгої переваги: