29. Статистичні методи

Статистичні методи.

Експертиза 1 (Е1): , – експерти ізольовані, – обернений зв'язок відсутній, .

Тобто результуюча числова оцінка знаходиться за формулою середньозваженого значення (математичного сподівання випадкової величини). За степінь узгодженості думок експертів служить дисперсія: .

Як модифікація (Е1) розглядається наступна експертиза 2: , = , де – "оптимістична" оцінка -го експерта, – "реалістична" і – "песимістична". Для експерта – "реаліста" (психологічний тип експерта можна визначити відповідним тестуванням) доцільно покладати , , 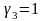; для експерта – "оптиміста" , , (він "завищує" оптимістичну оцінку), для експерта – "песиміста" , , (він "занижує" оптимістичну оцінку). Степінь узгодженості між оцінками визначається величиною

,

де , – степінь невпевненості -го експерта у своїй оцінці (для експерта реаліста , для інших – ).

В експертизах , можна визначити статистичну значимість отриманих результатів. Задаємо ймовірність похибки , вважаючи, що величина розподілена за нормальним законом з центром 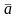і дисперсією . Тоді: , де , величина має розподіл Ст'юдента з -м ступенем свободи (визначаємо за таблицею розподілу Ст'юдента, за величиною р).

Опишемо застосування метода Делфі для Е1 у вигляді наступної експертизи 3: , .

Відображення задається наступним чином. Весь інтервал допустимих значень величин, що оцінюються, розбивається на інтервалів: . Експерт оцінює ймовірність попадання величини, що оцінюється, у кожен з інтервалів. Нехай – оцінка ймовірності попадання у – й інтервал, що дається – м експертом. Тоді ймовірність попадання величини в інтервал на основі думок усіх експертів оцінюється величиною: , .

За колективну оцінку приймається медіана побудованого розподілу, яка визначається з умови: .

Емпірично встановлено, що процедуру можна зупиняти, коли діапазон квантілів (де , ) зменшився в 1.6 рази у порівнянні з початковим.

Експертиза 4 полягає у співставленні індивідуальним ранжуванням експертів колективного ранжування: {множина всіх перестановок m об'єктів}, експерти ізольовані, обернений зв'язок відсутній.

Відображення визначається наступним чином. Кожен експерт задає місце (ранг) кожного об'єкта: – ранг - го об'єкта, визначеного - м експертом. Об'єкти впорядковуються у відповідності з величинами , (сума рангів кожного об'єкта по всіх експертизах; вважаємо, що експерти мають рівну компетентність) – на перше місце ставиться об'єкт з мінімальним і т.д. Колективне ранжування може бути нестрогим (ми розглядаємо випадок строгих індивідуальних ранжувань).

Степінь узгодженості думок експертів визначається за допомогою "коефіцієнта конкордації" , що визначається нижче. Розглянемо два крайніх випадки:

• ранжування всіх експертів співпадають;

• усі ранжування відмінні (вважаємо, що !).

Оскільки (експерти задають ранги від 1 до ), то "середній ранг" і за узгодженість експертів приймають суму квадратів відхилень від середнього значення . Коефіцієнтом конкордації для випадку строгих індивідуальних ранжувань називається величина:

.

У випадку нестрогих індивідуальних ранжувань (Експертиза 5) об'єктам, які "ділять" місця, приписуються рівні ранги (так, якщо два об'єкти ділять місця 2–3, то кожен з них отримує ранг 2.5).

Коефіцієнт конкордації для нестрогого ранжування:

,

де – число груп рівних рангів, введених - м експертом; – кількість об'єктів у - й групі, введеної - м експертом.

Статистичну значимість ранжування перевіряють наступним чином. Вибирається допустима ймовірність похибки ; вважається, що величина має – розподіл з – м степенем свободи. За таблицею розподілу знаходиться і, якщо , то отримане ранжування вважається статистично значимим (тобто значимим є узгодженість думок експертів). Якщо експерти не рівнокомпетентні, – вага -го експерта, то , інші формули залишаються без змін (оскільки ).

Експертиза 6 визначається для задачі знаходження колективного ранжування за нестрогими індивідуальними ранжуваннями за допомогою попарних порівнянь об'єктів.

Множина така ж, як і в ; експерти ізольовані, обернений зв'язок відсутній, – множина всіх матриць , де , ( ), , . Кожен експерт робить порівнянь, порівнюючи кожен об'єкт з кожним. Результат порівнянь -го експерта представляється матрицею розмірності , у якій тоді й лише тоді, коли для -го експерта об'єкт переважає об'єкт . Для будь-якої пари об'єктів або перший переважає другого, або навпаки; за визначенням.

Матриця , що задається - м експертом ( ), є матрицею деякого бінарного відношення, котре називається відношенням переваги - го експерта. Очевидно, що бінарне відношення, що задається матрицею є повним, антирефлексивним, антисиметричним і, взагалі кажучи, не є ациклічним.

Визначення 2.1. Відношення переваги з матрицею може бути виражене рангами, якщо всі об'єкти, упорядковані так, що тоді й лише тоді, коли ранг -го об'єкта менший за ранг .

Теорема 2.1. Необхідною й достатньою умовою того, що перевага виражається рангами, є ациклічність відношення переваги.

Теорема 2.2. Властивості відношень переваги приводять до еквівалентності умов ациклічності та наявності циклів довжини 3.

Відображення в Е6 визначається наступним чином. Будується матриця , де – матриця оцінок -го експерта. Знаходяться величини 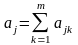, . Об'єкт з максимальним отримує ранг 1 (він переважає максимальну кількість інших об'єктів) і т.д.

Коефіцієнтом сумісності думок експертів називається величина:

де – число циклів довжини 3 у матриці . Величину для матриці можна використовувати у якості оцінки компетентності -го експерта.