8. Работа гибких стержней на центральное сжатие

Центральным сжатием называется случай, когда равнодействующая внешних сил проходит через центр изгиба.

Если при сжатии исключена возможность потери устойчивости, то стержень проверяется на прочность по тем же формулам, что и растянутый стержень:

.

В металлических конструкциях применяются гибкие стержни, теряющие свою несущую способность от потери устойчивости. Поэтому предельным напряжением гибкого сжатого стержня является критическое напряжение потери устойчивости состояния.

Гибкие прямые упругие стержни, подверженные действию осевой сжимающей силы, могут иметь две формы устойчивого состояния (рис. 23):

1) прямолинейную – когда стержень остается прямым ;

2) криволинейную – при искривленной оси стержня .

Рис. 23. Гибкий стержень при центральном сжатии

При незначительном увеличении нагрузки искривление стержня начинает быстро нарастать и стержень теряет несущую способность.

С некоторым запасом нормы рассчитывают стержни по критической силе по формуле Эйлера:

,

где – расчетная длина стержня;

– коэффициент приведения полной длины стержня к расчетной, за- висящий от условия закрепления концов стержня и его нагружения. Принимается по СНиП II-23-81*.

Критические напряжения определяются по формуле:

,

где – гибкость стержня, ;

i – радиус инерции, .

Формула Эйлера получена в предположении постоянного значения модуля упругости Е (рис. 24). Это имеет место до тех пор пока , так как при большем напряжении при наличии пластических деформаций модуль упругости становится переменным. Из условия можно получить то минимальное значение гибкости, при котором формула Эйлера справедлива:

.

Рис. 24. Диаграмма работы стали

При гибкостях меньше для данной марки стали потеря устойчивости происходит в упругопластической стадии работы материала при . Пока стержень сохраняет прямолинейную форму, напряжения распределяются равномерно по сечению. При отклонении стержня от прямолинейного состояния на эти напряжения накладываются напряжения изгиба. Со стороны дополнительного сжатия от изгиба материал работает в упругопластической стадии, со стороны растягивающих напряжений от изгиба материал работает упруго. Таким образом, при волокна на выпуклой стороне стержня разгружаются по упругому закону, на вогнутой же стороне они догружаются с модулем Е^, определяемым наклоном касательной в диаграмме работы в точке (рис. 25).

Рис. 25. Гибкий стержень при центральном сжатии в упруго-пластической

стадии работы

Поскольку , то нейтральная ось изгиба смещается в сторону растягивающих напряжений.

Положение нейтральной оси можно определить из условия равновесия:

.

При выпучивании на величину е, момент внешних сил получает приращение:

,

а момент внутренних сил: .

Если , то состояние устойчивое; если , то состояние неустойчивое, стержень теряет несущую способность; если , то состояние критическое (безразличное).

Ясинский Ф.С. показал, что формула Эйлера применима и в этом случае, если модуль упругости Е заменить приведённым модулем Т:

,

где – моменты инерции сжатой (догружаемой) и растянутой (разгружаемой) при выпучивании части сечения относительно нейтральной оси;

I – момент инерции сечения.

Согласно СНиП II-23-81* проверка устойчивости центрально-сжатого стержня выглядит так:

или

Из формулы Эйлера видно, что не зависит от марки стали, то есть Е для всех сталей одинаков. Поэтому критическое напряжение является функцией гибкости.

Наши нормы вводят понятие условной гибкости: .

Практически невозможно получить строгое сжатие стержня. Сопряжение элементов, даже ассиметрия сечения элементов всегда приводит к наличию эксцентриситетов, это так называемые случайные или конструктивные эксцентриситеты, которые нельзя заранее определить. Поэтому наши нормы представляют коэффициент , где , ;

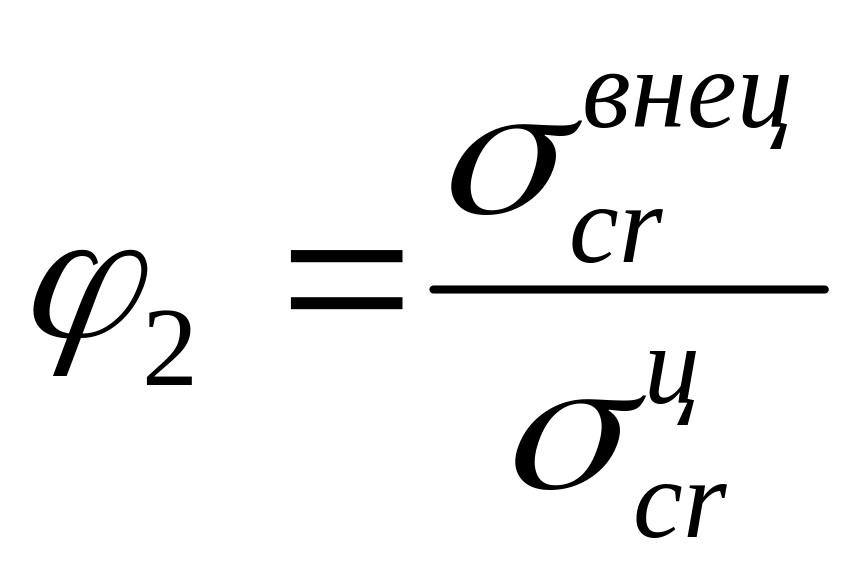– при центральном сжатии критическое напряжение, вычисленное в предположении строго центрального сжатия;

– критическое напряжение при наличии случайных небольших эксцентриситетов.