24. Описание технологических процессов как объектов управления (на примере уровня)

Объект регулирования уровня жидкости всегда следует рассматривать как двухъемкостной, так как резервуар непосредственно соединен с датчиком.

Определение периода колебании уровня жидкости. Для анализа колебании уровня жидкости рассмотрим работу резервуара с измерительной камерой (рис. 1), пренебрегая гидравлическим сопротивлением, возникающим при перетоке жидкости.

Р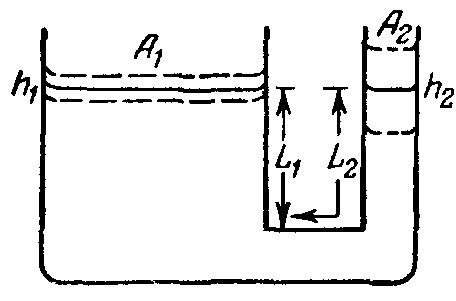 ис. 1. Колебания уровня жидкости в резервуаре с измерительной камерой

Допустим, что уровень жидкости в измерительной камере мгновенно возрастает по сравнению с уровнем жидкости в резервуаре системы. Уравнение возникающих при этом сил имеет следующий вид:

(1)

где h₁, А₁, М₁ и u₁ — соответственно высота, площадь, масса и скорость жидкости в резервуаре; h₂, A₂, М₂ и и₂ — те же величины в измерительной камере; — удельный вес жидкости. Из уравнения сплошности потока имеем:

Кроме того

где L₁ — уровень жидкости в резервуаре; L₂ — длина столба жидкости в измерительной камере и соединительной линии (см. рис. 1). Подставив значения u_1, М₁ и М₂ в уравнение (1), получим

(2)

Выразим уровень жидкости в измерительной камере h₂ через уровень h, соответствующий равновесному состоянию системы:

Подставив значение h_x из последнего равенства в уравнение (2), найдем изменение уровня h₂ в измерительной камере относительно уровня h:

где и₂ — скорость изменения уровня dh₂/dt. Исключив и₂, получаем

(3)

Полученное дифференциальное уравнение описывает поведение системы второго порядка, в которой отсутствуют силы трения.

Период собственных колебаний уровня жидкости в U-образном сосуде равен

(4)

Заметим, что зависит только от суммарного расстояния между уровнями (L₁ + L₂), аналогично периоду колебаний математического маятника, который также является функцией только его длины и ускорения силы тяжести.

Период собственных колебаний жидкости на поверхности резервуара диаметром L равен

(5)

• Заметим, что период собственных колебаний любого контура регулирования, включающего колебательный элемент, не может превышать периода собственных колебаний последнего. При этом колебательный элемент, независимо от степени демпфирования, дает сдвиг по фазе, равный 90°. Так как при регулировании уровня жидкости фазовый сдвиг равен 90°, то при наличии колебательного элемента общий сдвиг объекта по фазе составит 180°. Демпфирование же колебаний в измерительной камере дросселированием потока с помощью клапана на соединительной линии не изменяет период колебаний, а лишь уменьшает их амплитуду.

26. Расчет настройки регулятора.

Рассмотрим порядок расчетов для основных типовых законов регуляторов. Пусть задана структура типового регулятора и желаемый показатель колебательности M_жел.

П-регулятор должен обеспечить такой коэффициент пропорциональности k_пр, при котором амплитудно-фазовая характеристика разомкнутой системы будет касаться окружности с M_жел.

Вне зависимости от масштаба графиков окружность с M_жел всегда касается прямой, проведенной из начала координат в третьем квадранте под углом

α = arcsin(1/M_жел) (4.18)

к отрицательной вещественной полуоси. Точка касания прямой к окружности с M_жел соответствует координате 1 вещественной оси. При величине k_пр, соответствующему запасу устойчивости системы, окружность с заданным M_жел должна одновременно касаться амплитудно-фазовой характеристики разомкнутой системы и луча под углом α к отрицательной полуоси. С учетом изложенного расчет производится графоаналитическим методом в следующем порядке.

Вначале строится амплитудно-фазовая характеристика объекта W_oб(jω) и из начала координат проводится луч под углом α к отрицательной вещественной полуоси. Затем подбирается окружность с центром на вещественной отрицательной оси, касающаяся одновременно амплитудно-фазовой характеристики объекта и луча.

Определим модуль координаты точки касания лучом новой окружности |l|. Можно написать соотношение

|l|k_пр = 1, (4.19)

откуда находим k_пр = 1/|l|.

ПИ-регулятор рассчитывается аналогично П-регулятору с отличием в том, что амплитудно-фазовые характеристики разомкнутой системы строят из условия k_пр = 1 и для нескольких фиксированных значений k_и.

На основании соотношения (4.19) для каждого фиксированного значения k_и рассчитываются коэффициенты пропорциональности k_пр. Среди допустимых решений можно выбрать такие, которые обеспечивают наибольшее произведение k_прk_и.

ПИД-регулятор рассчитывается по такой же схеме, как и ПИ-регулятор. Для построения амплитудно-фазовых характеристик разомкнутой системы принимается равным единице k_пр и задается несколько фиксированных значений k_и, k_D, или их соотношение k_и : k_D. Далее подбираются окружности, которые касаются луча и амплитудно-фазовых характеристик. Затем из точек касания окружностями луча восстанавливаются перпендикуляры на вещественную ось и находятся коэффициенты k_пр на основании уравнения (4.19), а из полученных вариантов  соотношения коэффициентов k_пр, k_и, k_D будем отдавать предпочтение условию: k_прk_и→ max.