21. Устойчивость систем. Критерии устойчивости линейных непрерывных систем

Критерии устойчивости АСР. Известны несколько таких критериев. Наиболее употребительны алгебраические критерии Рауса– Гурвица, основанные на рассмотрении системы неравенств, образуемых из коэффициентов характеристического уравнения, а также связанные с частотными представлениями критерии Михайлова и Найквиста.

Проверка устойчивости по критерию Рауса – Гурвица сводится⁴¹ к вычислению по коэффициентам характеристического уравнения так называемых определителей Гурвица, которые для устойчивой системы управления должны быть положительными. Иными словами, система устойчива, если определители составленные из коэффициентов уравнения , положительны при

Для получения определителей Гурвица составляется таблица из коэффициентов характеристического уравнения n-й степени:

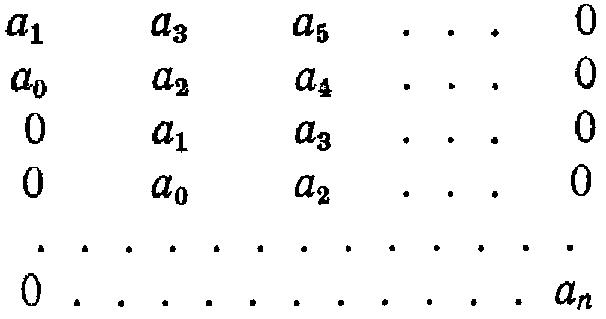
Правила составления таблицы, по главной диагонали выписывают по порядку п коэффициентов характеристического уравнения от а₁ до а_п каждая строка содержит п элементов; строки с нечетными и четными индексами чередуются; недостающие элементы строк заполняются нулями. Отчеркивая соответствующие строки и столбцы таблицы, получим п определителей Гурвица:

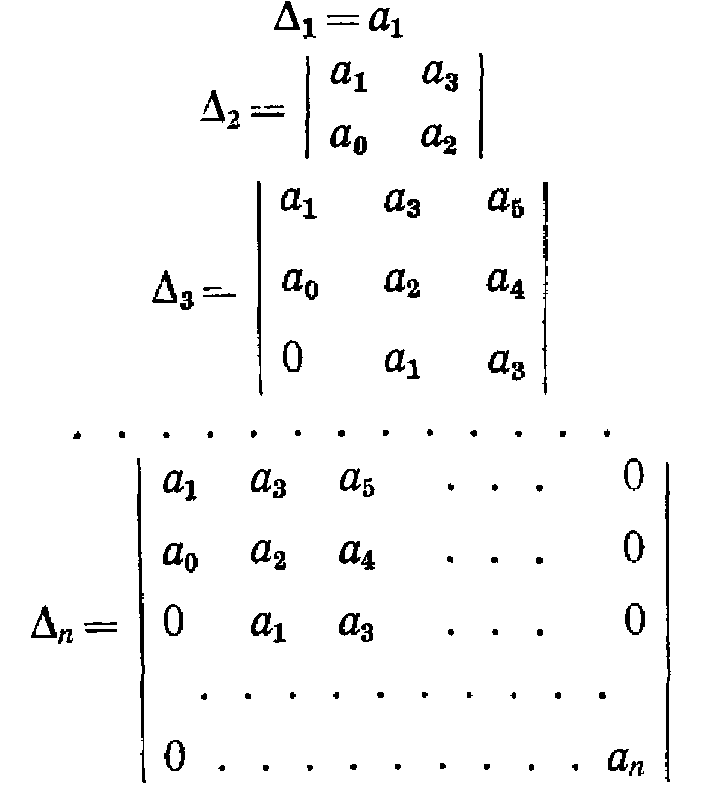
Достоинством критерия устойчивости Payca–Гурвица являются его сравнительная простота и небольшой о(5ъем вычислений при невысоком порядке дифференциального уравнения системы. Для систем более высокого порядка п > 4 использование этого критерия затруднительно ввиду значительного объема вычислений. В таких случаях применяют Другие критерии, использующие частотные характеристики АСР.

Критерий Найквйста – Михайлова позволяет судить об устойчивости замкнутой системы регулирования по амплитудно-фазовой характеристике разомкнутой системы, что дает возможность использовать для оценки устойчивости результаты экспериментальных исследований.

Критерий устойчивости Найквйста–Михайлова формулируют следующим образом: замкнутая система устойчива, если амплитудно-фазовая характеристика разомкнутой системы не охватывает на комплексной плоскости точку с координатами X ( ) = (–1,0).

На рис. 65, б изображены амплитудно-фазовые характеристики

р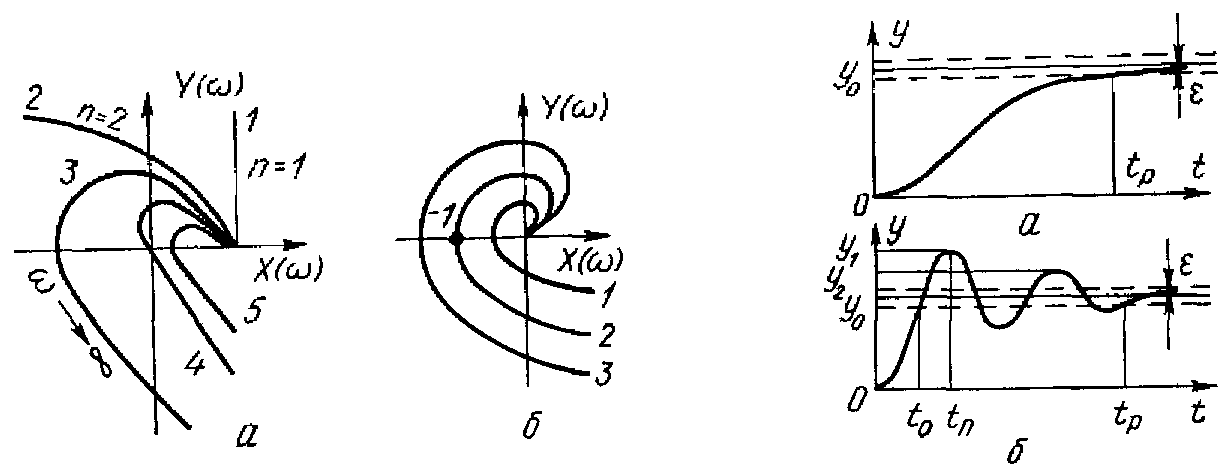 азомкнутых систем, которые в замкнутом состоянии устойчивы –

Рис. 65. Характеристики систем регулирования:

а – годографы замкнутых систем регулирования; б – амплитудно-фазовые характеристики разомкнутых систем

Рис. 66. Кривые, характеризующие качество переходных процессов: апериодического (с), колебательного (б) 1, неустойчивы – 3 или находятся на границе устойчивости – 2

На устойчивость системы значительное влияние оказывает запаздывание. Запаздывание в реальных технологических объектах затрудняет работу автоматических систем регулирования и ухудшает качество их работы. Объясняется это тем, что воздействие регулятора на вход объекта зависит от значения регулируемой величины на выходе объекта в данный момент. Однако за время, обусловленное запаздыванием, состояние объекта может измениться, и воздействие регулятора, еще не воспринявшего это изменение, может быть направлено в сторону усиления возмущений на входе объекта, а не в сторону их устранения. Запаздывание в объекте увеличивает отклонение регулируемой величины от заданного значения, удлиняет переходный процесс и может привести к неустойчивому состоянию.