Лекция 4 Вольт-амперная характеристика p-n-перехода

Выражение для вольт - амперной характеристики можно вычислить на основе некоторых следующих допущений: 1) приближения обеднённого слоя с резкими границами, т.е. контактная разность потенциалов и приложенной напряжение уравновешенны заряженными слоями n- и р- типа, вне которых полупроводник считается нейтральным; 2) приближения Больцмана, т.е. в обеднённой области справедливы распределения Больцмана, приводящие к выражениям (2.7); 3) приближения низкого уровня инжекции, т.е. когда плотность инжектированных носителей мала по сравнению с концентрацией основных носителей; 4) отсутствия в обедненном слое токов генерации и постоянства протекающих через него электронного и дырочных токов.

Преобразуя выражения (2.7) найдем:

(4.1а)

, (4.1б)

где  и  - потенциалы соответствующие середине запрещённой зоны и уровню Ферми ( = E_i/q,  = E_F/q). (Для отдельных полупроводников n- и р- типа уровень Ферми Е_F у каждого свой). В состоянии теплового равновесия произведение np равно n_i². Но при подаче напряжения на переход по обеим его сторонам происходит изменение концентрации неосновных носителей за счёт инжекции с обеих сторон перехода и произведение np уже не равно n_i². Раз течет ток, то уровень Ферми не одинаков по структуре и значения полученных уровней (квазиуровней Ферми) определяются из выражений:

(4.2а)

, (4.2б)

где _n и _р - квазиуровни (потенциалы) Ферми для электронов и дырок соответственно. Выразим их:

(4.3а)

, (4.3б)

Из (4.2) найдём (4.4)

При прямом смещении (_p-_n) > 0 и pn > n_i², а при обратном смещении (_p-_n) < 0 и pn < n_i².

для определения тока воспользуемся выражением (2.13)

=( учтем, что E  ) =

= . Представим и с учетом (4.2а) = .

Градиент потенциала . С учетом этого = .

Т.е. мы получили для электронного тока J_n:

(4.5)

Аналогично для дырочного тока имеем:

(4.6)

Мы получили, что плотности электронного и дырочного токов пропорциональны градиентам квазиуровней Ферми для электронов и дырок соответственно. В состоянии теплового равновесия =0 и J_n=J_p=0.

Зонная диаграмма с квазиуровнями Ферми, распределением потенциала и концентрации носителей в переходе показаны на рисунке 4.1

Рисунок 4.1 Зонная диаграмма с собственным уровнем Ферми , квазиуровнями Ферми для электронов и дырок _n и _p, распределение потенциала и концентрации носителей/

 - при прямом смещении; б – при обратном смещении.

Разность электростатических потенциалов на pn переходе определяется величиной

(4.7)

Для концентрации электронов в р- области на границе перехода при х =  х_р запишем, используя (4.7) и (4.4):

, (4.8)

где n_p0 - равновесная концентрация электронов в р - области

Аналогично

(4.9)

p_n - концентрация дырок в n - области на границе обеднённого слоя при х=х_n, а p_n0 - равновесная концентрация дырок в n - области.

Воспользуемся последними выражениями для определения связи тока с напряжением.

Для этого воспользуемся следующими представлениями о протекании тока. Дырки, попадая через обеднённую область в п/п n- типа рекомбинируют с электронами за время жизни _р, так, что скорость рекомбинации U будет равна

,

Этот инжекционный ток на границе обеднённой области при х=х_n , там где электрическое поле равно нулю (см. рис. 3.4), определяется диффузией дырок изменением градиента концентрации дырок в n области, так что можно записать:

(4.10)

Уравнение (4.10) представляет собой уравнение непрерывности в условиях отсутствия электрического поля и при неизменном состоянии тока (стационарном состоянии). Его также называют уравнением диффузии. Действительно, левую часть можно интерпретировать, как изменение концентрации дырок во времени, а правую - как перераспределение дырок в том же объёме, где изменяется концентрация. Именно так и происходит диффузия. (Второй закон Фика для диффузии).

Т.к. , запишем:

или (4.11)

Заметим, что ; L – представляет собой диффузионную длину, характеризующую расстояние, которое проходит носитель за своё время жизни до рекомбинации.

Стационарное уравнение (4.11) - это обыкновенное линейное уравнение второго порядка. Его решение представляет собой сумму экспонент:

,

Заметим, что концентрация избыточных носителей для х = , т.е. р() = 0, значит коэффициент первого слагаемого А₁=0. Для х=х_n А₂=р(x_n), отсюда:

учитывая, что . р(х_n) =p_n (4.9) получим:

(4.12)

Учитывая (2.11) при х=х_n (когда поле Е=0) плотность дырочного тока равна

(4.13)

(При выводе формулы (4.13) мы учли, что )

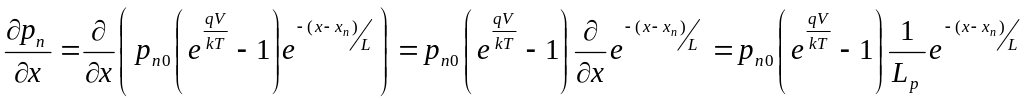Аналогично, рассматривая р- область, получим плотность электронного тока

(4.14)

Общий ток через переход равен сумме токов (4.13) и (4.14):

, (4.15)

Где + (4.16)

Выражения (4.15-4.16) представляют собой известную формулу Шокли, описывающую вольт-амперную характеристику идеального диода (рисунок 4.2)

Рисунок 4.2 – Вольт-амперные характеристики идеального pn перехода,

 - линейный масштаб;

б – полулогарифмический масштаб. (Здесь ток при обратном смещении помещён в тот же квадрант, что и при прямом)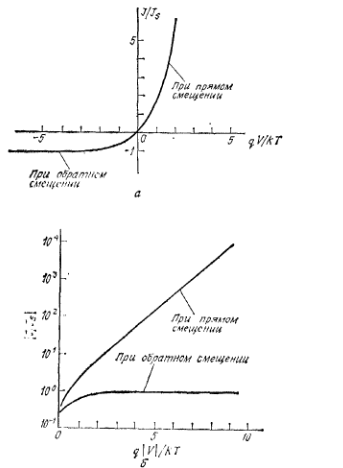

При прямом смещении (подаче на р- область положительного напряжения) при V > 3kT/q наклон характеристики идеального перехода постоянен, как видно из рис. 4.2б, а при обратном смещении плотность тока насыщается и становится равной J_s.

При ослаблении допущений, выдвинутых в начале лекции, при которых рассматривался pn переход, прямая и обратная ветки ВАХ отличаются от идеальных, описываемых выражениями (4.15) и (4.16).