Лекция 3 Электронно-дырочные переходы

Комбинация двух полупроводниковых слоёв с разным типом проводимости обладает выпрямляющими или вентильными свойствами: она гораздо лучше пропускает ток в одном направлении, чем в другом. Метод получения ионно-имплантированного перехода представлен на рисунке 3.1

Рисунок 3.1 - Ионно-имплантированный pn переход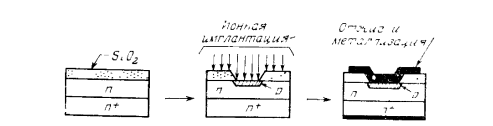

Как видно из рисунка, для изготовления Р⁺n диода необходимо взять полупроводник N⁺ типа (кремний n+ типа), вырастить эпитаксиальный слаболегированный слой n - типа, затем окислить поверхность, вскрыть определенное место в окисле, провести ионную имплантацию примеси Р-типа (бор), затем создать металлизацию к области Р+ типа и к обратной стороне подложки как контактные области. В итоге мы получим резкий несимметричный резкий pn переход, в котором есть высоколегированная Р+ область и низколегированная n область, как видно на левой части рисунка 3.2, которую можно интерпретировать как очень резкую границу между областями и однородным распределением примеси в n- и р- областях, как приведено на правой части рисунка 3.2

Рисунок 3.2 - Концентрационный профиль слева и его интерпретация в виде ступенчатого перехода с резким распределением примеси справа.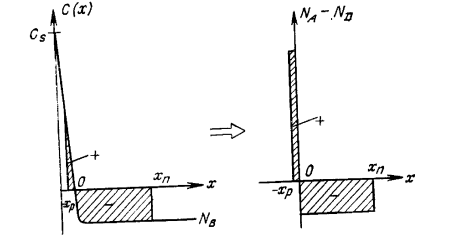

(как правило рассматривается ещё «плавный переход», в котором концентрация примеси на границе раздела n и p- типа меняется линейно с расстоянием)

Дырки из слоя Р+ типа диффундируют в низколегированную область n- типа. При этом в слое n-типа вблизи металлургической границы (область, где концентрации дырок и электронов равны) окажутся избыточные дырки. Они будут рекомбинировать с электронами до тех пор пока не будет выполнено условие равновесия (2.5). Соответственно концентрация электронов в этой области уменьшиться и "обнажаться"нескомпентсированные положительные заряды донорных атомов. Слева от металлургической границы "обнажаться" нескомпенсированные отрицательные заряды акцепторных атомов, от которых ушли дырки (см. рис. 3.3)

Рисунок 3.3 - Резкий pn переход при тепловом равновесии.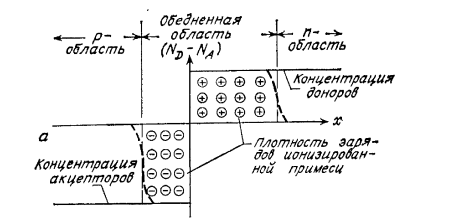

Можно заметить, что в одностороннем переходе, т.е. , где, как в рассматриваемом случае, концентрация дырок в Р- области р_р0 значительно больше, чем концентрация электронов в N- области n_n0 или р_р0 >> n_n0 перемещение электронов существенно меньше.

Область объёмных зарядов называют обеднённым слоем, имея в виду резко пониженную концентрацию свободных носителей в её обеих частях, причем их настолько мало, что при анализе перехода ими можно пренебречь. Вследствие малости свободных носителей можно считать обеднённую область самой высокоомной частью всей диодной структуры.

Переход в целом нейтрален: положительный заряд в правой части равен отрицательному заряду в левой части. Однако плотности зарядов резко различны (из-за различия в концентрации примесей). Поэтому и различны протяженности обеднённых слоёв: в слое с меньшей концентрацией примеси ( в нашем случае в n- слое) область обеднённого заряда значительно шире. В таком случае справедливо утверждение , что "несимметричный переход сосредоточен в высокоомном слое.

Наличие зарядов в обеднённой области приводит к возникновению электрического поля, как показано на рисунке 3.4

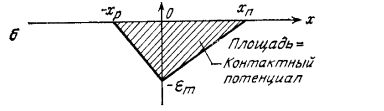
Рисунок 3.4 - Электрическое поле Е_m в обеднённой области.

Ток в состоянии равновесия (без приложения внешнего напряжения) в переходе не течет (там нет подвижных носителей), вследствие отсутствия градиента электрохимического потенциала (уровня Ферми E_F), как показано на рисунке 3.5:

Рисунок 3.5 - Зонная диаграмма pn перехода.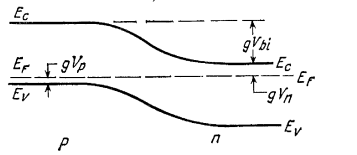

На рисунке 3.5 видно, что в правой части уровень Ферми E_F близко подходит к краю зоны проводимости Е_С , что означает, что это область n- типа, а в левой части Ферми E_F близко подходит к краю валентной зоны Е_v , что означает, что это область P- типа. Постоянство уровня Ферми во всём объёме приводит к изгибу зон pn перехода на величину V_bi, которую называют контактной разностью потенциалов.

Из рисунка 3.5 следует, что V_bi представляет собой разницу между уровнями Ферми не соединённых между собой полупроводников n- типа и р- типа. Тогда с учетом выражений (2.7), получим:

(3.1)

С учётом того, что концентрация электронов в n- области n_n0 определяется в основном концентрацией полностью ионизированных доноров N_Д, а концентрация дырок в Р- области p_p0 определяется концентрацией полностью ионизированных акцепторов N_A , запишем:

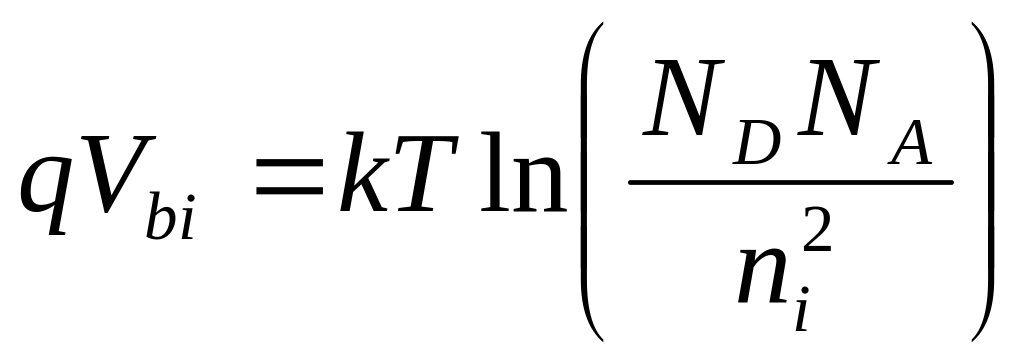(3.2)

Для типичного случая, когда N_A=10¹⁹ см^-3 и N_Д=10¹⁶ см^-3, k=1,3710^-23Дж/С, q=1,610^-19 Кл, получим, что V_bi=0.83B – такова контактная разность потенциалов при образовании pn перехода.

При тепловом равновесии электрическое поле в нейтральных частях полупроводника равно нулю. Поэтому общий отрицательный заряд на единицу площади в р- области равен общему положительному заряду на единицу площади в n- области:

, (3.3)

Здесь x_n и x_p - размеры обеднённых областей.

Чтобы рассчитать величину электрического поля Е(х) в обеднённой области и её протяженность x_n+x_p воспользуемся уравнением , связывающим распределение потенциала V с зарядом  – одномерным уравнением Пуассона:

, (3.4)

где _s - диэлектрическая проницаемость полупроводника, _s=₀, где ₀ - диэлектрическая проницаемость вакуума ₀ =9*10^-14 Ф/см,  - относительная диэлектрическая постоянная полупроводника (для кремния  = 11,9).

В общем случае плотность заряда  в полупроводнике записывается следующим образом:

,

где и - концентрации ионизированных примесей.

Для области n- типа можно записать:

, (3.5а)

для р- области:

(3.5б)

Интегрируя выражение (3.5б) по х в пределах от х=0 до х=х_p получим распределение напряжённости электрического поля в обеднённой области р-типа:

(3.6а)

аналогично для выражение (3.5а) получим:

(3.6б)

Мы получили линейное распределение электрического поля в обеднённой области, которое приведено на рисунке 3.4. Можно заметить, при х=0 электрическое поле принимает максимальное значение:

(3.7)

Учитывая (3.7), выражение (3.6б) можно выразить, как

Далее, ещё раз интегрируя выражения (3.6), получим распределение потенциала:

;

Мы получили квадратичное распределение потенциала, что приведено на рисунке 3.6

Рисунок 3.6 - распределение потенциала по обе стороны от границы перехода (х=0)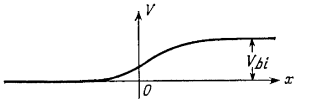

Приравнивая значения V(x) при x=0 и учитывая V_p-V_n=V_bi получим:

или, учитывая (3.7) запишем

или , (3.8)

где W - полная ширина обеднённой области.

Определим связь ширины обеднённой области с концентрациями примеси по обе стороны pn перехода.

Из (3.8) с учётом (3.7) запишем:

, а также:

, перенесём x_n и x_p в правые части и сложим оба выражения:

. Т.к. x_n+x_p=W, то выразим W:

(3.9)

Для несимметричного перехода , в котором N_A  N_D можно записать:

(3.10)

т.е. ширина pn перехода определяется концентрацией примеси в высокоомной области.

Полагая V_bi =0.83B и N_D = 10¹⁶ см-3, получим для кремния Wx_n 0.3 мкм

С учётом подаваемого обратного напряжения V на pn переход, можем записать:

(3.11)

т.е. ширина перехода возрастает с напряжением.