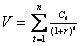7. Внутренняя стоимость финансовых активов: понятие, подходы к оценке.

Внутренняя стоимость –ценность фин. актива с позиции конкретного участника рынка.

«Цена — это то, что ты платишь, а стоимость — это то, что ты получаешь».

Цена ( P ) и внутренняя стоимость ( V ) – абсолютные величины, которые не только меняются в динамике, но, с позиции конкретного инвестора, нередко могут не совпадать. Различие цены и стоимости финансового актива проявляется в следующих моментах:

стоимость – это расчетный показатель; цена – декларированный, т. е. объявленный, который можно видеть в прейскурантах, котировках;

в любой момент времени цена однозначна; стоимость многозначна, при этом число оценок стоимости зависит от числа профессиональных участников рынка;

в условиях равновесного рынка цена, во-первых, количественно выражает внутренне присущую активу стоимость; во-вторых, стихийно устанавливается как среднее из оценок стоимости, рассчитываемых инвесторами.

Очевидно, в каждый данный момент возможны три ситуации:

1)  P > V- продавать , 2)  P < V - покупать , 3)  P = V .

Подходы:

1) Фундаменталистская – внутренне присущая любому финансовому активу стоимость может быть количественно оценена как дисконтированная стоимость будущих поступлений, генерируемых этим финансовым активом. По значениям предполагаемых поступлений и продолжительности периода прогнозирования, который может быть как конечным (например, для срочной облигации), так и бесконечным (например, для акции), можно рассчитать текущую внутреннюю стоимость любого финансового актива, базируясь на некоторой процентной ставке r (ставке дисконтирования) , которая может быть равна ожидаемой доходности актива.

2) Технократический подход –(формальный), (рассматривается прошлый опыт). Надо знать динамику в прошлом и предсказывать поведение сейчас. Когда рассматривается статистика и переносится на будущее.

3) Теория ходьбы наугад – (нет смысла предсказывать, ориентироваться нужно на реальные цены). Текущая цена всегда вбирает всю необходимую информацию. Будущие ожидания отражаются в текущей цене. Предсказать невозможно.

Внутренняя стоимость финансового актива – приведенная стоимость всех наличных денежных потоков, которые владелец актива рассчитывает получить в будущем

Наиболее распространенным и чаще всего используемым потенциальными инвесторами является фундаменталистский подход, согласно которому текущая внутренняя стоимость ( V ) любого финансового актива в общем виде может быть рассчитана по формуле:

(2.2.1)

 

где ct— ожидаемый денежный поток в t -м периоде (обычно год);

n — горизонт прогнозирования

r — приемлемая (ожидаемая или требуемая) доходность.

8. Оценка внутренней стоимости акции.

Среди финансовых активов выделяются так называемым капитальные финансовые активы — акции и облигации. Именно с помощью этих инструментов формируется капитал фирмы, они являются одновременно и объектами, и способами реализации двух типовых финансовых процессов — мобилизации (с помощью эмиссии акций и облигаций привлекается капитал на долгосрочной основе) и инвестирования (в акции и облигации вкладываются свободные денежные средства как в долгосрочных, так и в краткосрочных целях).

модель оценки акций, основанную на дисконтировании дивидендов, выплачиваемых в денежной форме:

(2.2.4)

где V а — теоретическая (внутренняя) стоимость обыкновенной акции;

Dk — выплаченный дивиденд в k-м периоде;

г — коэффициент дисконтирования.

Сложность применения этой формулы связана с невозможностью точно предсказать величину будущих дивидендов. Исключение составляют привилегированные акции. Привилегированные акции генерируют доход неопределенно долго, равными выплатами через равные промежутки времени, т.е. поток платежей представляет собой бессрочный аннуитет. Поэтому их текущая теоретическая стоимость, равная приведенной доходности, определяется по формуле (2.1.18):

V па = D / r ,

(2.2.5)

где V па – внутренняя стоимость привилегированной акции;

D – величина дивиденда, в рублях;

r – рыночная норма прибыли по акциям данного класса риска.

Эмиссия бессрочных привилегированных акций, предусматривающих выплату дивиденда по постоянной ставке, является довольно рисковым мероприятием, поскольку невозможно спрогнозировать процентные ставки на длительную перспективу. Поэтому иногда привилегированные акции эмитируются на условиях, позволяющих эмитенту выкупить их в определенный момент времени по соответствующей цене, называемой ценой выкупа (Рв). В этом случае текущая теоретическая стоимость таких акций определяется по формуле:

(2.2.6)

• где V пав – внутренняя стоимость выкупаемой привилегированной акции;

• D – величина дивиденда, в рублях;

• r – рыночная норма прибыли по акциям данного класса риска;

• n – число периодов до выкупа акций эмитентом;

• Рв – выкупная цена акции.

Что касается обыкновенных акций, то известны различные методы их оценки; наиболее распространенным из них является метод, основанный на оценке их будущих поступлений, т.е. на применении формулы (2.2.4). В зависимости от предполагаемой динамики дивидендов конкретное представление формулы меняется. Базовыми являются три варианта динамики прогнозных значений дивидендов:

• дивиденды не меняются (ситуация аналогична ситуации с привилегированными акциями, т.е. применяется формула

• дивиденды возрастают с постоянным темпом прироста;

• дивиденды возрастают с изменяющимся темпом прироста.

Рассмотрим оценку акций с равномерно возрастающими дивидендами

Предполагается, что базовая величина дивиденда (т.е. последнего выплаченного дивиденда) равна D; ежегодно она увеличивается с темпом прироста g . Например, по окончании первого года будет выплачен дивиденд в размере D × (1 + g ) и т.д. Тогда формула (2.2.1) примет вид:

(2.2.7)

Используя формулу суммы членов геометрической прогрессии, можно показать, что:

(2.2.8)

где Vаор – внутренняя стоимость обыкновенной акции с равномерно возрастающими дивидендами;

D 0 – дивиденд в базисном периоде;

g – темп прироста дивидендов (в долях от единицы);

r – ставка дисконтирования;

D 1 – дивиденд в первом прогнозном периоде.

Данная формула имеет смысл при r > g и называется моделью Гордона.